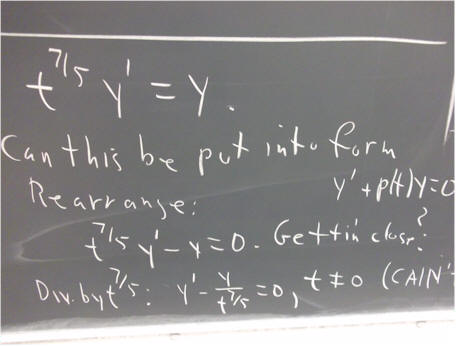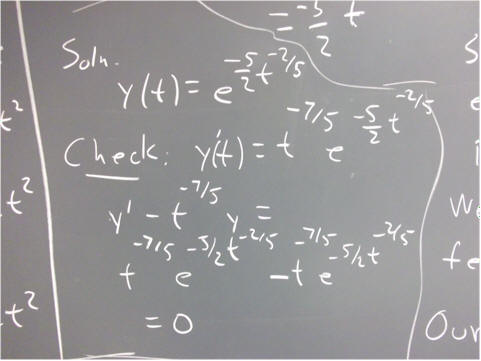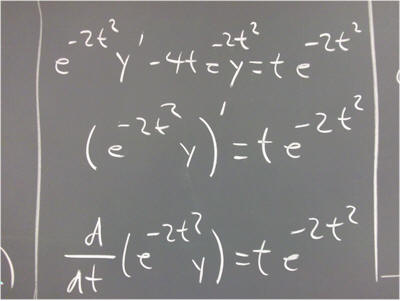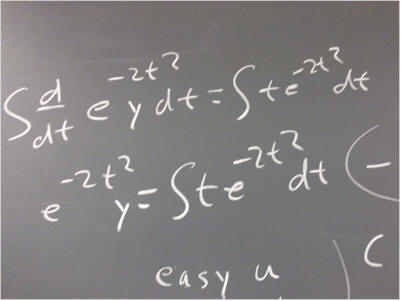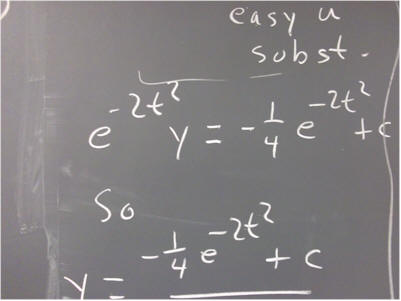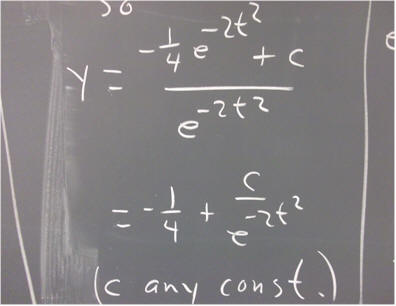110124 Differential Equations

Class Notes 1/24/11 Class.

Note:  Do not submit this document.  The q_a_ for this assignment contains the same questions, but is formatted slightly differently to make it viewable by the program I use to review documents.  When you insert your answers to questions prior to submitting the document, use the q_a_ version, just a click or two away on your Assignments Page.

This document and the next are supplemented by Chapter 2 of the text.

We show the following:

• y ' + t y = 0 has solution y = e^(-t).

If y = e^(-t) then y ' = -t e^(-t) so that

y ' + t y becomes -t e^-t + t e^-t, which is zero.

• y ' + sin(t) y = 0 has solution y = e^(cos t)

If y = e^(cos t) then y ' = -sin(t) e^(cos(t)) so that

y ' + t y becomes -sin(t) e^(cos(t)) + sin(t) e^cos(t) = 0

• y ' + t^2 y = 0 has solution y = e^(-t^3 / 3)

This is left to you.

• What do all three solutions have in common?

Some of this is left to you. 

However for one thing, note that they all involve the fact that the derivative of a function of form e^(-p(t)) is equal to -p'(t) e^(-p(t)).

And all of these equations are of the form y ' + p(t) y = 0.

Now you are asked to explain the connection.

What would be a solution to each of the following:

• y ' - sqrt(t) y = 0?

If we integrate sqrt(t) we get 2/3 t^(3/2).

The derivative of e^( 2/3 t^(3/2) ) is t^(1/2) e^ ( 2/3 t^(3/2) ), or sqrt(t) e^( 2/3 t^(3/2) ).

Now, if we substitute y = sqrt(t) e^( 2/3 t^(3/2) ) into the equation, do we get a solution?  If not, how can we modify our y function to obtain a solution?

• sqrt(t) y ' + y = 0?

The rest of our equations started with y ' .  This one starts with sqrt(t) y '.

We can make it like the others if we divide both sides by sqrt(t).

We get y ' + 1/sqrt(t) * y = 0.

Follow the process we used before. 

We first integrated something.  What was it we integrated?

We then formed an exponential function, based on our integral.  That was our y function.  What y function do we get if we imitate the previous problem?

What do we get if we plug our y function into the equation?  Do we get a solution?  If not, how can we modify our y function to obtain a solution?

• t y ' = y?

If we divide both sides by t and subtract the right-hand side from both sides what equation do we get?

Why would we want to have done this?

Imitating the reasoning we have seen, what is our y function?

Does it work?

• y ' + p(t) y = 0 has solution y = e^(- int(p(t) dt)).

This says that you integrate the p(t) function and use it to form your solution y = e^(- int(p(t) dt)).

Does this encapsulate the method we have been using?

Will it always work?

What do you get if you plug y = e^(-int(p(t) dt) into the equation y ' + p(t) y = 0?

Is the equation satisfied?

y ' + p(t) y = 0 is the general form of what we call a first-order linear homogeneous equation.  If it can be put into this form, then it is a first-order linear homogeneous equation.

Which of the following is a homogeneous first-order linear equation?

• y * y ' + sin(t) y = 0

We need y ' to have coefficient 1.  We get that if we divide both sides by y.

Having done this, is our equation in the form y ' + p(t) y = 0?

Is our equation therefore a homogeneous first-order linear equation?

• t * y ' + t^2 y = 0

Once more, we need y ' to have coefficient t.

What is your conclusion?

• cos(t) y ' = - sin(t) y

Again you need y ' to have coefficient 1.

Then you need the right-hand side to be 0.

Put the equation into this form, then see what you think.

• y ' + t y^2 = 0

What do you think?

• y ' + y = t

How about this one?

Solve the problems above that are homogeneous first-order linear equations.

Verify the following:

• If you multiply the expression y ' + t y by e^(t^2 / 2), the result is the derivative with respect to t of e^(t^2 / 2) * y.

The derivative with respect to t of e^(t^2 / 2) * y is easily found by the product rule to be

(e^(t^2 / 2) * y) '

 = (e ^ (t^2 / 2) ) ' y + e^(t^2/2) * y '

= t e^(t^2/2) * y + e^(t^2 / 2) * y '.

If you multiply the expression y ' + t y by e^(t^2 / 2) you get e^(t^2 / 2) y ' + t e^(t^2 / 2).

Same thing.

Now, what is it in the original expression y ' + t y that led us to come up with t^2 / 2 to put into that exponent?

• If you multiply the expression y ' + cos(t) y by e^(sin(t) ), the result is the derivative with respect to t of e^(-sin(t)) * y.

Just do what it says.  Find the t derivative of e^(sin(t) ) * y.  Then multiply both sides of the expression y ' + cos(t) y by e^(sin(t) * y).

How did we get e^(sin(t)) out of the expression y ' + cos(t)?  Where did that sin(t) come from?

• If you multiply both sides of the equation y ' + t y = t by e^(t^2 / 2), the integral with respect to t of the left-hand side will be e^(t^2 / 2) * y.

You should have the pattern by now.  What do you get, and how do we get t^2 / 2 from the expression y ' + t y = t in the first place?

The equation becomes e^(t^2 / 2) * y ' + t e^(t^2 / 2) y = t e^(t^2 / 2).

The left-hand side, as we can easily see, is the derivative with respect to t of e^(t^2 / 2) * y.

So if we integrate the left-hand side with respect to t, since the left-hand side is the derivative of e^(t^2 / 2) * y, an antiderivative is e^(t^2 / 2) * y.

Explain why it's so.

Having integrated the left-hand side, we integrate the right-hand side t e^(t^2 / 2).

What do you get?  Be sure to include an integration constant.

Set the results of the two integrations equal and solve for y.  What is your result?

Is it a solution to the original equation?

• If you multiply both sides of the equation y ' + p(t) y = g(t) by the t integral of -p(t), the left-hand side becomes the derivative with respect to t of e^(-integral(p(t) dt) ) * y.

See if you can do this.