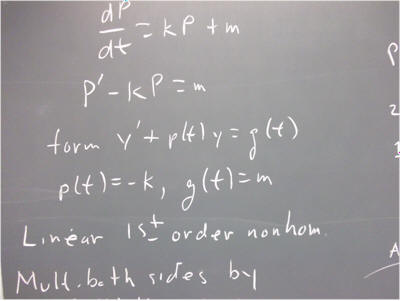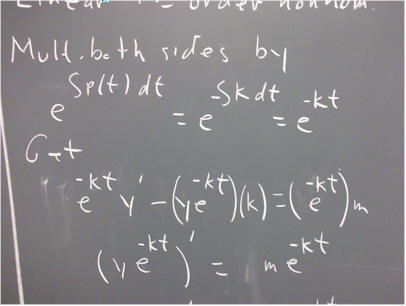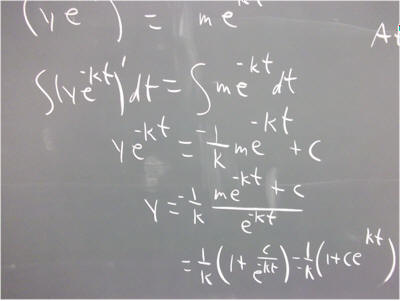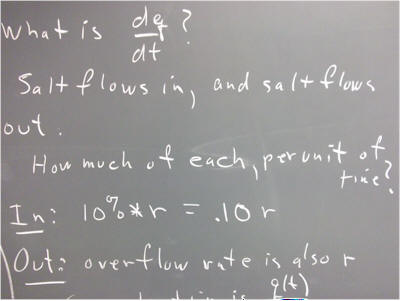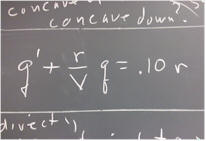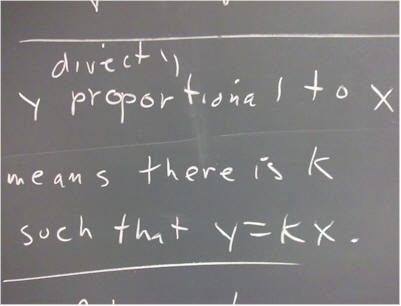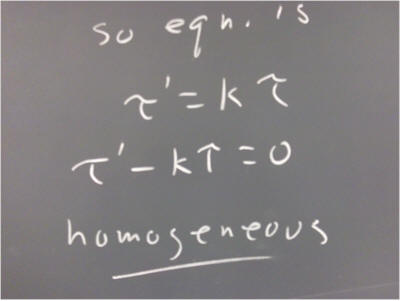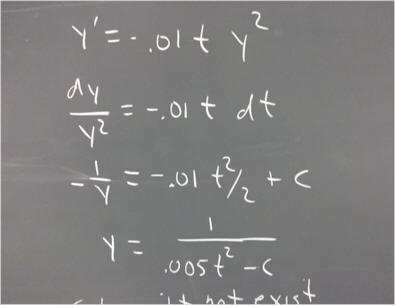110202 differential equations

Italicized problems are continued from the 1/31/11 class, and have the same numbers (e.g., `q004) as they did in that document. Non-italicized problems are preliminary to the 2/02 class and are numbered `q001, `q002, etc.. As a result some non-italicized questions have the same numbers as some italicized questions (e.g., `q004 appears for both sets).

It will be to your benefit to familiarize yourself with these questions, and you are invited to submit any part of this document prior to class on 2/02/11. However given the short time between Monday and Wednesday classes, this isn't a requirement.

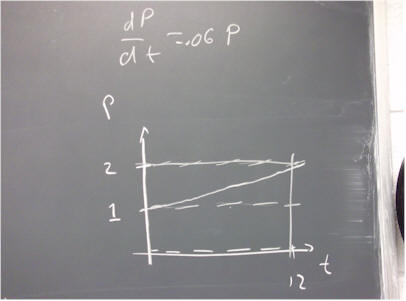
`q004 (from 110131). Assuming k = .06, sketch the direction field of the equation dP/dt = k P for P ranging from 0 to 2, and for t ranging from 0 to 12. Use an increment of 4 for t and an increment of .5 for P.

Based on your sketch, plot a variety of solution curves.

Each curve will leave the 'box' defined by 0 <= t <= 12, 0 <= P <= 2 at some point. Any solution curve must leave the box by the top and some by the right side. Be sure you have included curves with both properties.

All your curves can be extended to the left until they intersect the y axis. If necessary, extend your curves accordingly.

For three different curves, at least one of which exits the box to the right and at least one of which exits from the top, indicate the coordinates of the point at which the curve enters, and the point at which it exits.

****

#$&*

Sketch a curve which passes through the point (0, 1). At what point does this curve exit the box?

****

#$&*

Sketch the curve which exits the box through the top right-hand corner. At what point does this curve enter the box from the left?

****

#$&*

Describe the solution curve which passes through the origin.

****

#$&*

If P is principle in thousands of dollars, then what is the interpretation of each of the solution curves you have sketched? In particular be sure you have stated the meaning of the intercept of the graph with the P axis, and of the point at which the curve leaves the 'box'.

****

#$&*

Extending the preceding problem (new for 110202)

`q001 (110202):

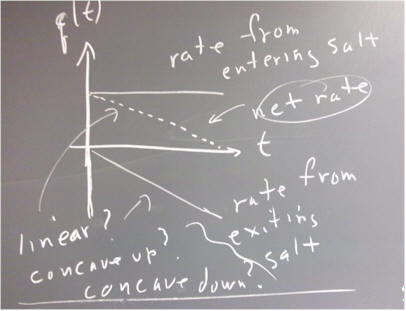
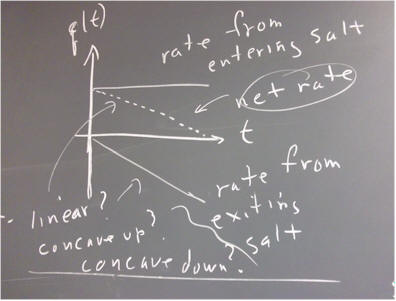
The direction field shown in the figure below applies to the equation dP/dt = k P, with k = .06.

For P = 2000, then what should be the slope of the direction field, according to the equation dP/dt = .06 P?

****

#$&*

Do the slopes here appear to match the slope you just calculated?

****

#$&*

The slope you should have obtained was over 100. The slopes on this direction field all appear to be less than 1. We need to either reconcile this, or discard the direction field of the figure.

Let's first check out a solution to the problem. As you can easily verify, dP/dt = k P gives us general solution P(t) = C e^(k t). To get the solution passing through the P axis at 2000, we apply the initial condition P(0) = 2000. Our particular solution for this initial condition is P(t) = 2000 e^(k t). Our direction field is for k = .06; for P(0) = 2000 our function is therefore P(t) = 2000 e^(.06 t). A graph of this function is consistent with the direction field.

Verify this. Following the trend of the direction field, estimate the likely value of P(3). What is your estimate?

****

#$&*

What do you get if you evaluate P(3)? Is this consistent with your estimate?

****

#$&*

According to the direction field, does the solution curve through (0, 2000) exit the box to the right or through the top?

****

#$&*

Check this out by evaluating P(12). What is your conclusion?

****

#$&*

Reasonable answers to these questions will tend to reinforce our confidence in the direction field.

Consider the direction field line through (8, 4000). Based on the scale of your graph, estimate the rise of that segment. It should be obvious that the run of the segment is 2. What therefore is the slope represented by that segment?

****

#$&*

The slope appears to be less than 1. Explain why that segment actually represents a slope in the hundreds.

****

#$&*

Construct the slope field for the equation dP/dt = .06 P, for the interval 10 000 <= P <= 20 000, 0 <= t <= 12. Scale your slope segments appropriately.

Based on your slope field, at what value of t do you estimate the value of P(t) will double, starting with P = 10 000 at t = 0?

****

#$&*

`q005 (from 110131). The equation dP/dt = k P + m is of the same form as y ' + p(t) y = g(t), with p(t) = -k and g(t) = m

Explain in detail why the equation is of this general form, specifically explaining how we get p(t) = - m and g(t) = m.

****

#$&*

This equation is therefore first-order linear and nonhomogeneous. We have learned the technique for solving such equations.

What is the general solution to our equation dP/dt = k P + m?

****

#$&*

`q006 (from 110131). I can mix a 10% salt solution into pure water by siphoning the salt solution from one bottle, into a second bottle which is initially full of pure water. The second bottle was initially full, so it will overflow.

We will make the simplifying assumption that the salt water flowing into the second bottle is instantly distributed equally throughout that bottle.

Assume that the rate of flow of salt solution is r (e.g., r might be, say, 7 cm^3 / second). The second bottle is assumed to have volume V (e.g., the second bottle might have a volume of 500 cm^3, corresponding to half a liter)

If q(t) is the amount of salt in the second bottle, as a function of clock time, then at what rate is salt leaving the bottle at clock time t?

****

#$&*

Express your preceding result as a differential equation, find the general solution of the equation, and find the particular solution for which r = 7 cm^3 / sec.

Question `q001 (non-italicized), for the 2/02/11 class, was given previously.

Subsequent questions are all non-italicized and are for the 2/02/11 class only.

`q002. A quantity y is directly proportional to a quantity x if there exists a constant k such that y = k x.

The rate, with respect to time, at which the temperature of an object left to cool in a room at temperature T_room is directly proportional to the difference between the temperature of the object, which we will represent by T(t), and the temperature of the room.

Letting T ' (t) stand for the rate at which the temperature T(t) changes with respect to clock time, write down the proportionality.

****

#$&*

You should have written down a differential equation. That equation is linear. Find its general solution.

****

#$&*

If the object has an initial temperature of 50 Celsius, and its temperature initially changes at -5 Celsius per minute when placed in a room at temperature 20 Celsius, then what is the specific function that models its temperature as a function of time?

****

#$&*

`q003. Consider the equation dy/dt = -.01 y^2.

Explain why we cannot solve this equation using the techniques we have been applying to first-order linear equations.

****

#$&*

We will see why shortly, but for now accept that this equation can be rearranged into the form

dy / y^2 = -.01* dt

and integrate both sides to get a general solution.

****

#$&*

`q004. Consider the equation dy/dt = -.01 t y^2. Algebraically rearrange this equation so that dy is a factor of one side, with all other y factors on that side, and dt, along with all other t factors, is on the other.

Integration both sides of the equation to get a general solution.

1/y = -.005 t^2 + c

y = 1 / (-.005 t^2 + c)

Find the particular solution for which y = 25 when t = 0.

****

#$&*

Show that the function f(t, y) = -.01 t y^2 is defined and continuous for all values of y and t.

****

#$&*

Show that there exist values of t for which your solution is neither defined nor continuous.

****

#$&*

While a linear equation of the form y ' + p(t) y = g(t) always has a solution which is defined and continuous, on any interval for which p(t) and g(t) are defined and continuous, this example shows that the same is not necessarily so for an equation of the form y ' + f(t, y) = 0. Explain this statement.

****

#$&*

`q005. The rate, with respect to time, at which the velocity of a spherical object moving through water changes is directly proportional to the square of its velocity.

Write this as a differential equation.

****

#$&*

Solve the equation.

****

#$&*

If the object is initially moving at 30 cm/s and changing velocity at the rate of 1000 cm/s^2, then what function describes its velocity?

****

#$&*

`q006. Recall implicit differentiation. If you need a review of implicit differentiation see the q_a_ document at http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa16.htm . If you need a review of the chain rule, see http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa12.htm and http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa13.htm .

If y is a function of t, then what is the derivative with respect to t of the function H(t, y) = t cos y + 1/y?

****