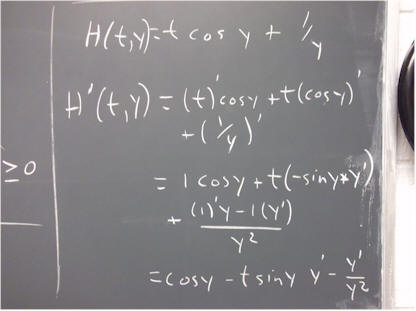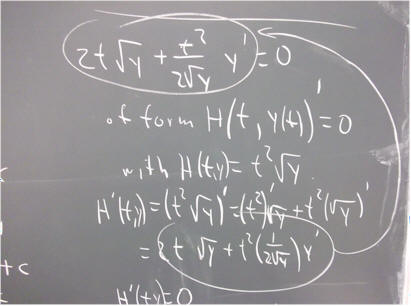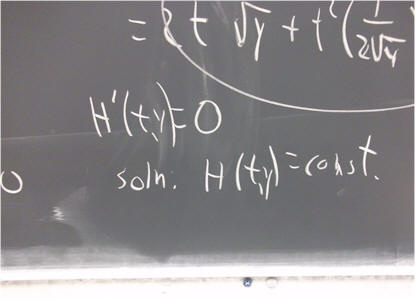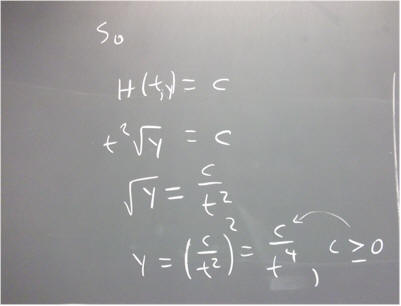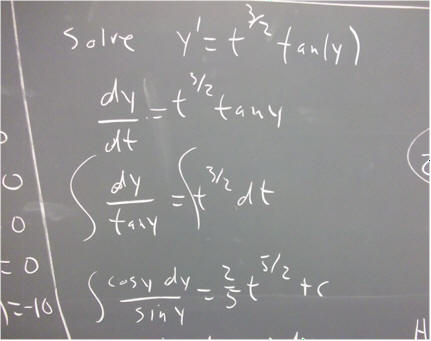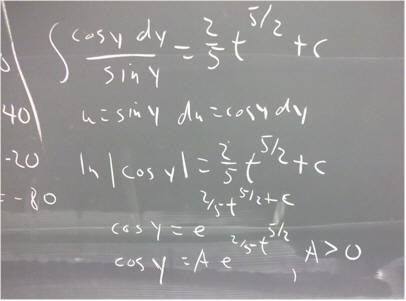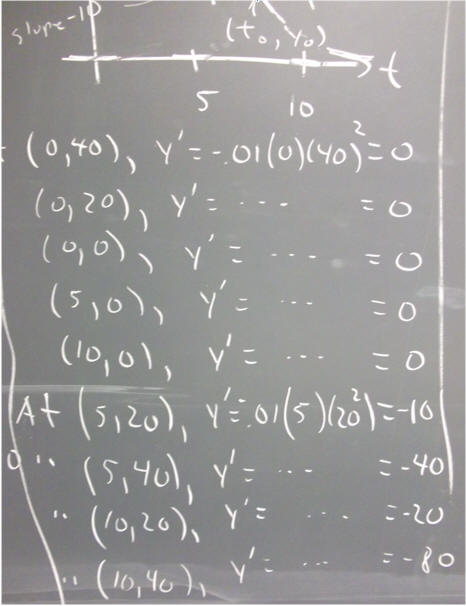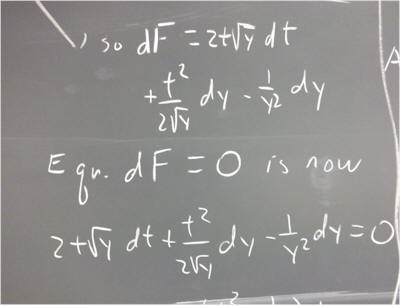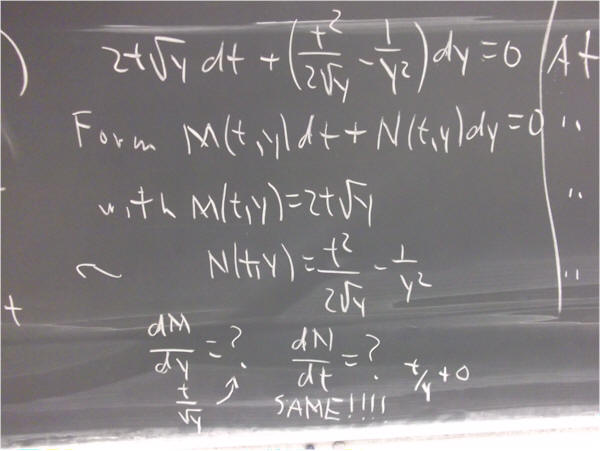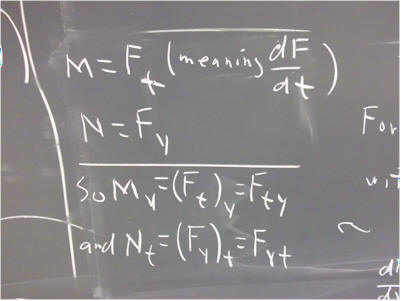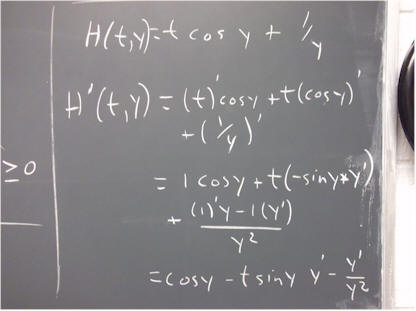
110207 differential equations
From 110202 questions
`q006. Recall implicit differentiation. If you need a review of implicit differentiation see the q_a_ document at http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa16.htm . If you need a review of the chain rule, see http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa12.htm and http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa13.htm .
If y is a function of t, then what is the derivative with respect to t of the function H(t, y) = t cos y + 1/y?
****
#$&*
`q007. Verify that the derivative of the function H(t, y) = t^2 sqrt(y) is 2 t sqrt(y) + t^2 / (2 sqrt(y) ) * y '.
****
#$&*
Verify that the equation
2 t sqrt(y) + t^2 / (2 sqrt(y) ) * y ' = 0
is of the form
( H(t, y) ) ' = 0,
where H(t, y) = t^2 sqrt(y) and ' indicates the derivative with respect to t.
****
#$&*
Verify that the equation
( H(t, y) ) ' = 0
is equivalent to the equation
H(t, y) = c,
where c is any constant number.
****
#$&*
For the given function H(t, y) = t^2 sqrt(y), solve the equation
H(t, y) = c
for y as a function of t.
****
#$&*
Show that this function y(t) satisfies the equation
2 t sqrt(y) + t^2 / (2 sqrt(y) ) * y ' = 0.
****
#$&*
New questions (separable, exact equations)
`q001. Solve the equation y ' = t^(3/2) tan(y) for the initial condition y(pi) = 1.
****
#$&*
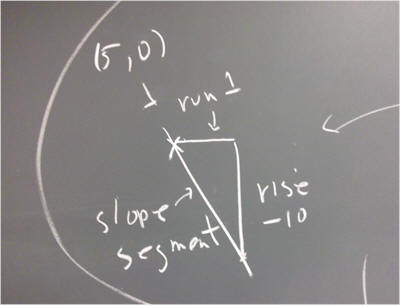
`q002. We saw previously that the equation y ' = -.01 t y^2 has solutions of the form y = 1 / (-.005 t^2 - c). For negative values of c this solution has a vertical asymptote at t = sqrt(200 c), and is not defined at t = sqrt(200 c).
We can understand why this equation has vertical asymptotes if we plot the direction field. Plot the direction field defined by t values 0, 2, 4, 6, 8 and 10, and y values 0, 10, 20, 30, 40. Explain what happens when you sketch solution curves from various points of this grid.
****
#$&*
`q003. The sort of thing that happened with the direction field of y = -.01 t y^2 cannot happen for a linear differential equation of the form y ' + p(t) y = 0, unless p(t) itself is undefined at a point. Explain why this is so.
****
#$&*
`q004. Write the equation ( y^2 cos(t) ) ' = 0 in the form f(t, y, y') = 0. (To do so, find the derivative of y^2 cos(t) and set it equal to zero).
****
#$&*
Show that this equation is solved by the function y for which y^2 cos(t) = c, where c is an arbitrary constant.
****
#$&*
`q005. Show that the equation
dF = 0,
where F is a function F(t, y), is of the form
N(t,y) dt + M(t, y) dx = 0.
where N(t, y) = F_t and M(t, y) = F_y.
****
#$&*
Show furthermore than N_y = M_t.
****
#$&*
`q006. Show that the equation
( sqrt(y) - e^t cos(y) + t ) dt + (t / (2 sqrt(y) + e^t sin(y)) dy = 0
is of the form
N dt + M dy = 0, with N_y = M_t.
****
#$&*
Integrate N with respect to t, recalling that since y is treated as a constant, the integration constant can be any function f(y).
****
#$&*
Integrate M with respect to y, recalling that since t is treated as a constant, the integration constant can be any function g(t).
****
#$&*
Show that these integrals can be made equal by making a good choice of f(y) and g(t).
****
#$&*
Let F(t, y) be the common integral of the two functions.
Show that our equation is of the form dF = 0.
****
#$&*
Argue that the solution is therefore of the form F(t, y) = c, for a constant c.
****
#$&*