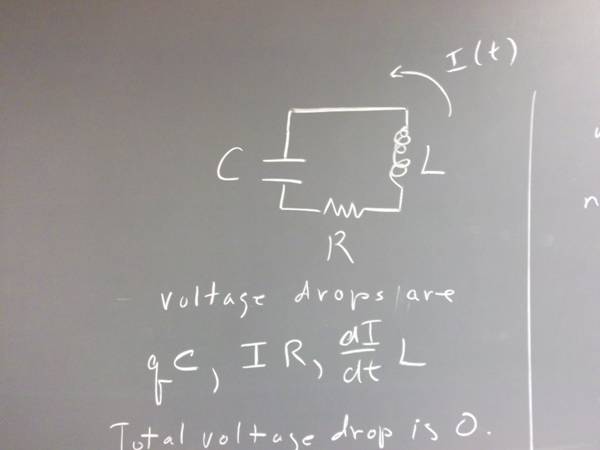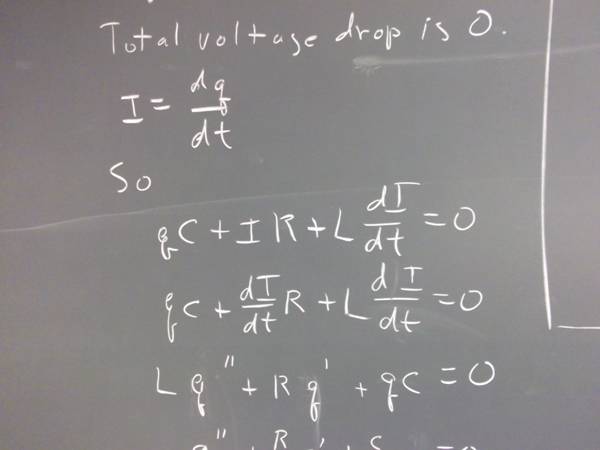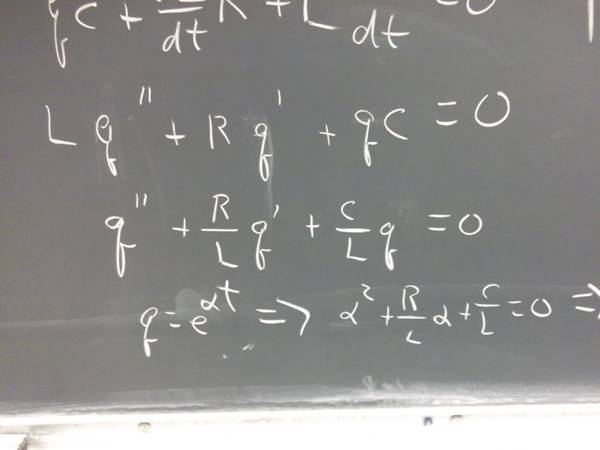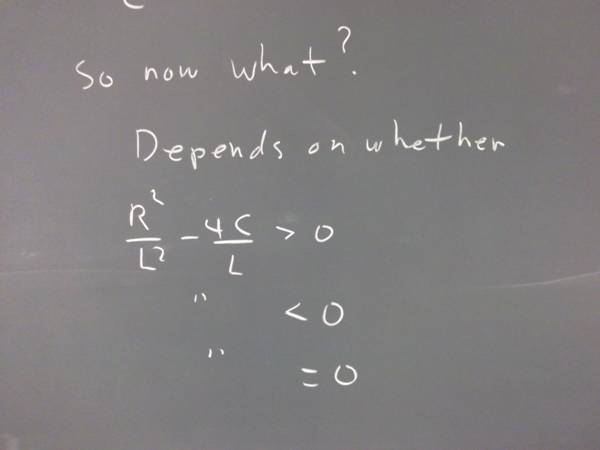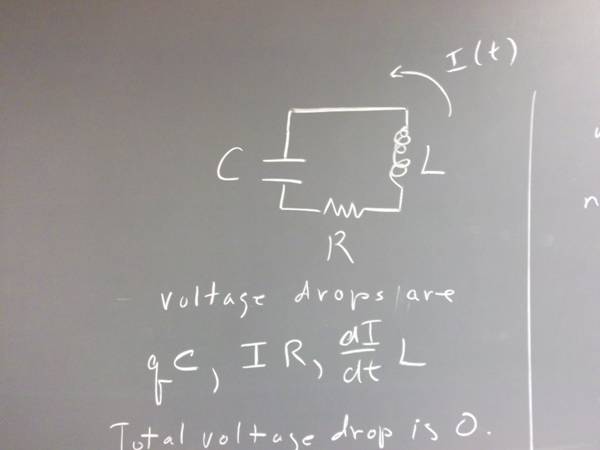
110228
From the preceding class:
`q007. The net force on a simple pendulum of mass m at position x is F_net = - k x - gamma x '. - k x is the restoring force (from physics we know that k = m g / L, and -gamma x ' is the drag force that results from air resistance).
We know that F_net = m * a = m * x ''.
****
#$&*
What therefore is the differential equation equivalent to the given force equation?
****
#$&*
Using trial solution x = e^(r t) find two linearly independent solutions of this equation, and show that they are linearly independent.
For today's class:
`q001. Find one solution to the equation
y '' - 2 y ' + y = 0.
****
#$&*
Why doesn't the usual method give us two solutions?
****
#$&*
Let your solution be denoted y_1(t).
Let y = u * y_1(t), where y_1(t) is the solution you found.
Find y ' and y '', and plug them into the original equation y '' - 2 y ' + y = 0.
****
#$&*
Simplify your equation.
Solve your equation for u.
****
#$&*
The function y = u * y_1(t) is a solution to the original equation.
Show by substitution into the original equation that it is so.
****
#$&*
Show that this new solution is linearly independent of your original solution y_1(t).
****
#$&*
`q002. In a certain circuit containing a capacitor, a resistor and an inductor, q stands for the charge on a capacitor, and the current is I = dq/dt.
The voltage drop across the capacitor is C q.
The voltage drop across the resistor is I * R.
The voltage drop across the inductor is L * dI/dt.
The sum of these voltage drops is 0.
Write this condition as a differential equation for the charge q.
****
#$&*
Solve the equation.
****
#$&*
Under what conditions are your solutions e^(r_1 t) and e^(r_2 t) real and distinct?
****
#$&*
Under what conditions are your solutions e^(r_1 t) and e^(r_2 t) identical?
****
#$&*
Under what conditions are your solutions e^(r_1 t) and e^(r_2 t) complex?
****
#$&*
Under what conditions are your solutions e^(r_1 t) and e^(r_2 t) both linear combinations of sine and cosine functions?
****
#$&*
`q003. For the preceding equation, in the case where both solutions are linear combinations of sine and cosine functions, let omega be the common angular frequency of those functions.
If we impose a harmonic voltage on the system, of the form V_0 sin( omega t), the equation becomes nonhomogeneous, with the sum of the voltages equal to V_0 sin(omega_1 t).
Write this equation.
****
#$&*
Now assume that y is a solution of this equation, of the form y = c_1 cos(omega t) + c_2 sin(omega t). Is it possible to evaluate the values of c_1 and c_2? If so, do. If not, explain why not.
****
#$&*
`q004. The equation x '' + gamma / m x ' + k x = 0, encountered in the preceding class notes, represents the motion of a damped pendulum for which air resistance exerts a damping force equal to - gamma * v, where v is the velocity of the pendulum.
How is this equation analogous to the present equation q '' + R / L q ' + C / L q = 0?
****
#$&*
A fundamental set for the first equation is
{ e^( (-gamma / m + sqrt( gamma^2 / m^2 - 4 k / m) ) / 2) t), e^( (-gamma / m - sqrt( gamma^2 / m^2 - 4 k / m) ) / 2) t) }
= { e^( (-gamma / m + sqrt( gamma^2 - 4 k ) ) / ( 2 m) ) t), e^( (-gamma / m - sqrt( gamma^2 - 4 k m) ) / (2 m) ) t) }
How is this similar in nature to the solution set for the equation q '' + R / L q ' + C / L q = 0 ?
****
#$&*
How therefore are the damped pendulum and the LRC circuit analogous?
****
#$&*
Solution to #7 from preceding class notes (damped pendulum)
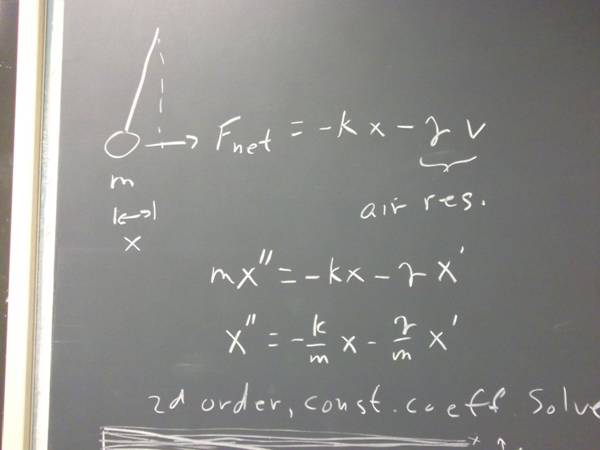
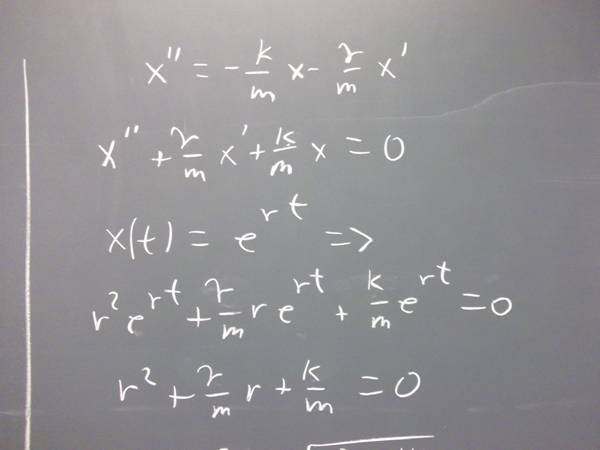


Solution to `q001 from current notes:

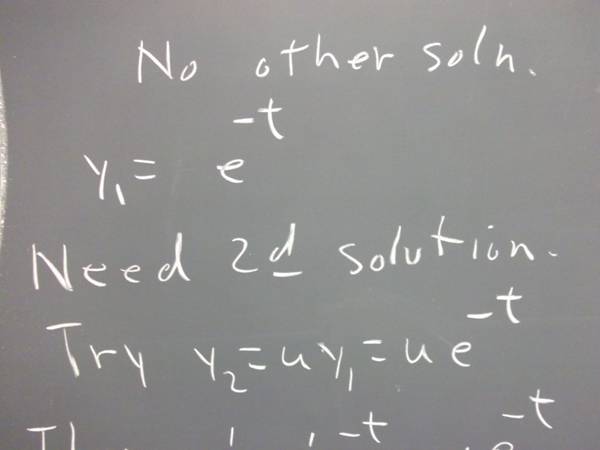
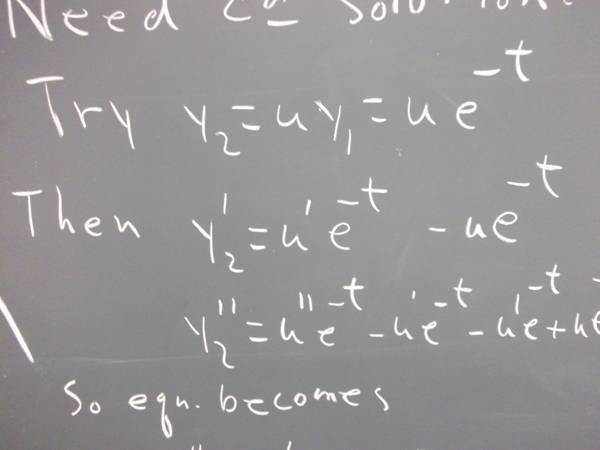
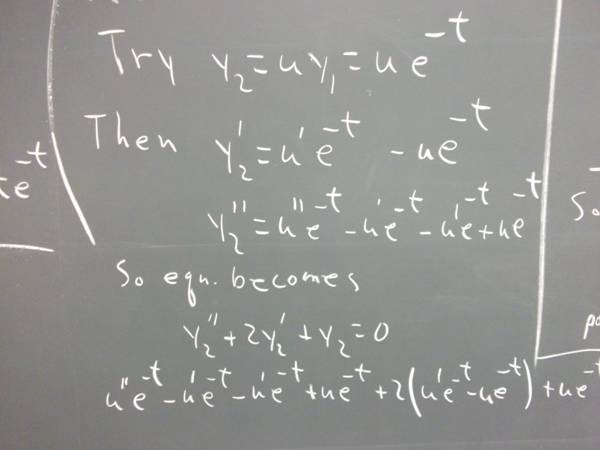


Solution to `q002 from current notes: