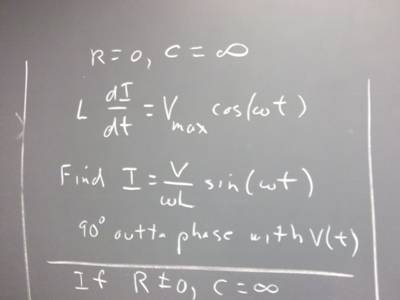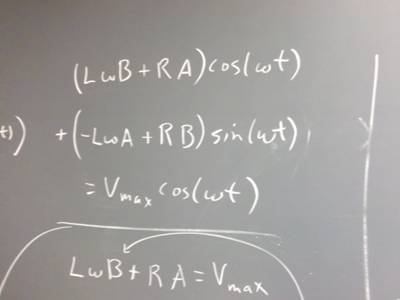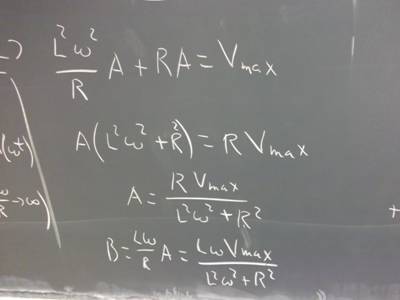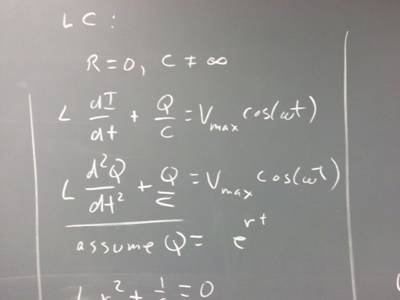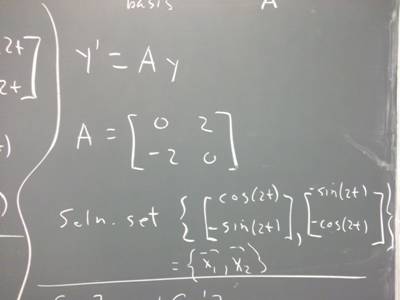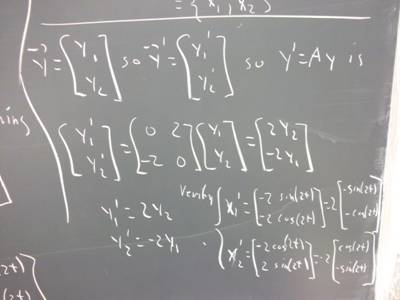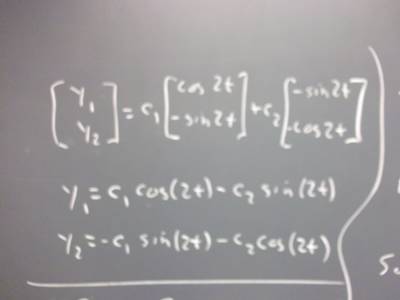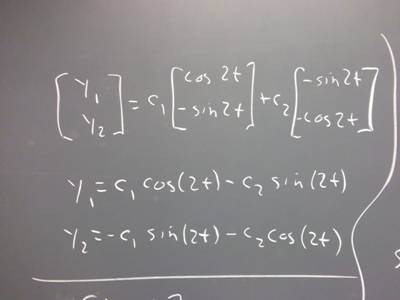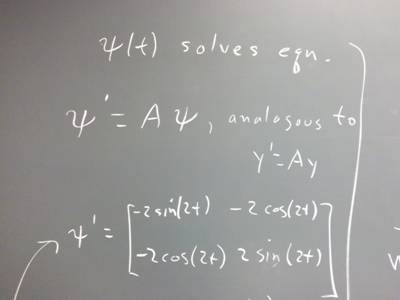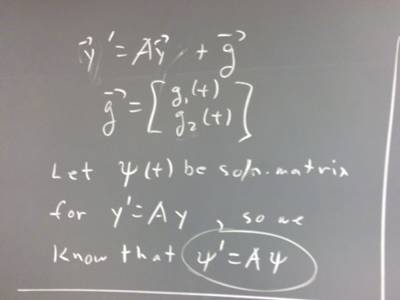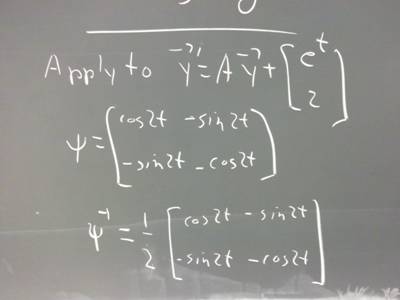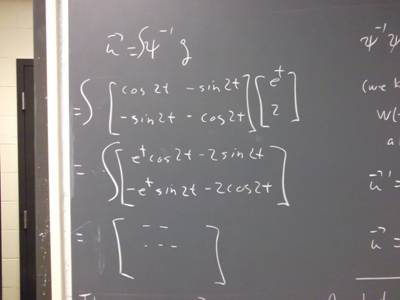
110425 Differential Equations
1. The equation y ' = A * y, for A = [0, 2; -2, 0] is found to have solution
set {[cos(2 t); -sin(2 t) ], [-sin(2 t); -cos(2 t)]}
Write the equation as a system of two equations in terms of the variables y_1
and y_2.
Give two linearly independent solutions y_1 and y_2 for this system, based on
the solution set as given above.
Give the fundamental set, based on your solutions y_1 and y_2.
Show that your fundamental set is really a fundamental set. If you have
correctly based your set on the solution set given above, it will be so.
2. For the equation given in the preceding, y_1 and y_2 were given a meaning in
terms of the system of equations.
Now we will consider y_1 to be the vector [cos(2 t); -sin(2 t) ], y_2 to be the
vector [-sin(2 t); -cos(2 t)].
write the matrix psi(t) = [y_1, y_2]
Show that this matrix solves the equation
psi ' (t) = A * psi(t).
3. If y_P = psi(t) u, where u = [u_1, u_2] and psi(t) is a solution matrix for
the system y ' = A y, then
what is the expression for y_P '?
If we substitute y_P ' into the equation
y ' = A y + g,
then what do we get?
Considering that y ' = A y, how does our equation simplify?
How would we use this to solve for the vector u?
Having found the vector u, how do we then find y_P?
4. Apply the above to the equation y ' = A y + [e^t; 2], with A = [0, 2; -2, 0
].
5. In 2-dimensional real space, let B1 = {v_1, v_2} = { [1; 0], [0; 1] } be the
standard basis.
Let B2 = {u_1, u_2} = { [1, 1], [1, -1] } be another basis.
Express the vector [2; 3] in the form c_1 v_1 + c_2 v_2.
What therefore is the vector [c_1; c_2]_B1 that expresses [ 2; 3] in terms of
the basis B1?
Now express the same vector in the form d_1 u_1 + d_2 u_2.
What therefore is the vector [d_1, d_2]_B2 that expresses [2, 3] in terms of the
basis B2?
If
u_1 = a_11 v_1 + a_12 v_2,
and
u_2 = a_21 v_1 + a_22 v_2,
then what are a_11, a_12, a_21 and a_22?
Show that if T is the 'transformation matrix'
T = [a_11, a_12; a_21, a_22]
then
T * [c_1; c_2] = [d_1; d_2].
... generalize ...