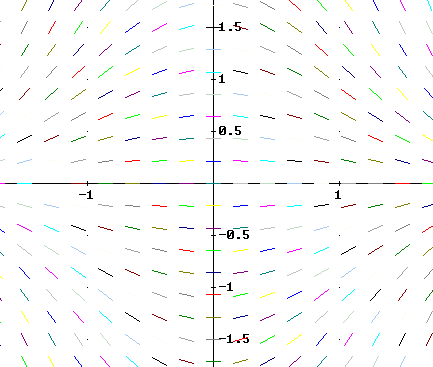
Section 2.2

Solve the following equations with the given initial conditions:

1.  y ' - 2 y = 0, y(1) - 3

****

#$&*

2.  t^2 y ' - 9 y = 0, y(1) = 2.

****

#$&*

3.  (t^2 + t) y' + (2t + 1) y = 0, y(0) = 1.

****

#$&*

4.  y ' + sin(3 t) y = 0, y(0) = 2.

****

#$&*

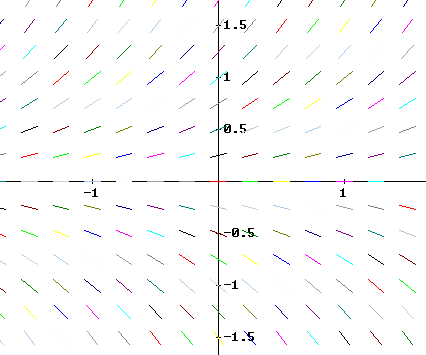
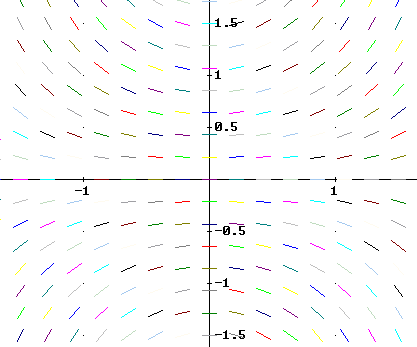
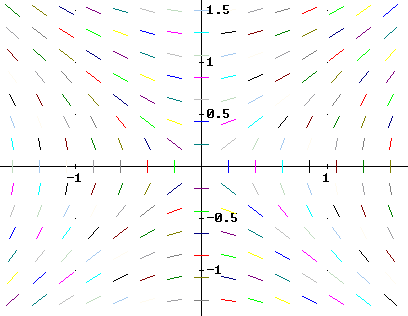
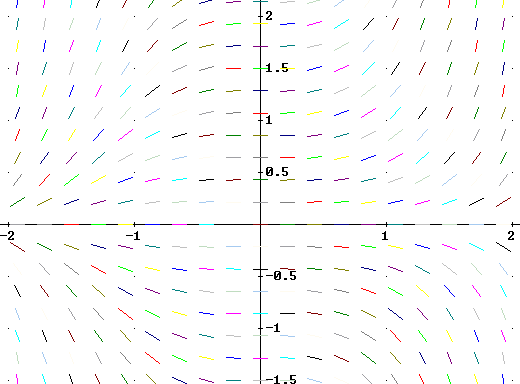
5.  Match each equation with one of the direction fields shown below, and explain why you chose as you did.

y ' - t^2 y = 0

****

#$&*

y ' - y = 0

****

#$&*

y' - y / t = 0

****

#$&*

y ' - t y = 0

****

#$&*

y ' + t y = 0

****

#$&*

A

B

C

D

E

F

6.  The graph of y ' + b y = 0 passes through the points (1, 2) and (3, 8).  What is the value of b?

****

#$&*

7.  The equation y ' - y = 2 is first-order linear, but is not homogeneous.

If we let w(t) = y(t) + 2, then:

What is w ' ?

****

#$&*

What is y(t) in terms of w(t)?

****

#$&*

What therefore is the equation y ' - y = 2, written in terms of the function w and its derivative w ' ?

****

#$&*

Now solve the equation and check your solution:

Solve this new equation in terms of w.

****

#$&*

Substitute y + 2 for w and get the solution in terms of y.

****

#$&*

Check to be sure this function is indeed a solution to the equation.

****

#$&*

8.  The graph below is a solution of the equation y ' - b y = 0 with initial condition y(0) = y_0.  What are the values of y_0 and b?

Section 2.3

Solve each equation:

1.  y ' + y = 3

****

#$&*

2.  y ' + t y = 3 t

****

#$&*

3.  y ' - 4 y = sin(2 t)

****

#$&*

4.  y ' + y = e^t, y (0)  = 2

****

#$&*

5.  y ' + 3 y = 3 + 2 t + e^t, y(1) = e^2

****

#$&*

6.  The general solution to the equation y ' + p(t) y = g(t) is y = C e^(-t^2) + 1, t > 0.  What are the functions p(t) and g(t)?

****

#$&*

Section 2.4.

1.  How long will it take an investment of $1000 to reach $3000 if it is compounded annually at 4%?

****

#$&*

How long will it take if compounded quarterly at the same annual rate?

****

#$&*

How long will it take if compounded continuously at the same annual rate?

****

#$&*

2.  What annual rate of return is required if an investment of $1000 is to reach $3000 in 15 years?

****

#$&*

3.  A bacteria colony has a constant growth rate.  The population grows from 40 000 to 100 000 in 72 hours.  How much longer will it take the population to grow to 200 000?

****

#$&*

4.  A population experiences growth rate k and migration rate M, meaning that when the population is P the rate at which new members are added is k P, but the rate at they enter or leave the population is M (positive M implies migration into the population, negative M implies migration out of the population).  This results in the differential equation dP/dt = k P + M.

Given initial condition P = P_0, solve this equation for the population function P(t).

****

#$&*

In terms of k and M, determine the minimum population required to achieve long-term growth.

****

#$&*

What migration rate is required to achieve a constant population?

****

#$&*

5.  Suppose that the migration in the preceding occurs all at once, annually, in such a way that at the end of the year, the population returns to the same level as that of the previous year.

How many individuals migrate away each year?

****

#$&*

How does this compare to the migration rate required to achieve a steady population, as determined in the preceding question?

****

#$&*

6.  A radioactive element decays with a half-life of 120 days.  Another substance decays with a very long half-life producing the first element at what we can regard as a constant rate.  We begin with 3 grams of the element, and wish to increase the amount present to 4 grams over a period of 360 days.  At what constant rate must the decay of the second substance add the first?

****

#$&*

2.5.

1.  A 3% saline solution flows at a constant rate into a 1000-gallon tank initially full of a 5% saline solution.  The solutions remain well-mixed and the flow of mixed solution out of the tank remains equal to the flow into the tank.  What constant rate of flow in necessary to dilute the solution in the tank to 3.5% in 8 hours?

****

#$&*

2. Solve the preceding question if the tank contains 500 gallons of 5% solution, and the goal is to achieve 1000 gallons of 3.5% solution at the end of 8 hours.  Assume that no solution is removed from the tank until it is full, and that once the tank is full, the resulting overflow is well-mixed.

****

#$&*

3.  Under the conditions of the preceding question, at what rate must 3% solution be pumped into the tank, and at what rate must the mixed solution be pumped from the tank, in order to achieve 1000 gallons of 3.5% solution at the end of 8 hours, with no overflow?

****

#$&*

4.  Under the conditions of the first problem in this section, suppose that the overflow from the first tank flows into a second tank, where it is mixed with 3% saline solution.  At what constant rate must the 3% solution flow into that tank to achieve a 4% solution at the end of 8 hours?

****

#$&*

5. In the situation of Problem #1, suppose that solution from the first tank is pumped at a constant rate into the second, with overflow being removed, and that the process continues indefinitely.  Will the concentration in the second tank approach a limiting value as time goes on?  If so what is the limitng value?  Justify your answer.

****

#$&*

Now suppose that the flow from the first tank changes hour by hour, alternately remaining at a set constant rate for one hour, and dropping to half this rate for the next hour before returning to the original rate to begin the two-hour cycle all over again.  Will the concentration in the second tank approach a limiting value as time goes on?  If so what is the limiting value?  Justify your answer.

****

#$&*

Answer the same questions, assuming that the rate of flow into (and out of) the tank is 10 gallons / hour * ( 3 - cos(t) ), where t is clock time in hours. 

****

#$&*

6.  When heated to a temperature of 190 Fahrenheit a tub of soup, placed in a room at constant temperature 80 Fahrenheit, is observed to cool at an initial rate of 0.5 Fahrenheit / minute. 

If at the instant the tub is taken from the oven the room temperature begins to fall at a constant rate of 0.25 Fahrenheit / minute, what temperature function T(t) governs its temperature?

****

#$&*

3.1

For each of the following equations, each of the form y ' = f(t, y), find the largest open set of the form a < t < b, alpha < y < beta which contains the point (t_0, y(t_0)) implied by the given initial condition, and for which the functions f and f_y are both continuous.

1.  y ' cos(y) - sqrt(t) = 0, y(pi) = 1

2.  (t^2 - 1) + (1 + y) y ' = 0, y(0) = 1

3.  cos(t) y ' = 1 - tan(y), y(pi/4) = 0

Write each equation in Problems 4-6 in the form y ' = f(t, y), calculate the y partial derivative f_y(t, y) and determine the regions in the plane in which both f and f_y are continuous.

4.  t y ' + e^y = 0

5.  sin(t) y ' + sqrt(y) = 0

6.  cot(t) y + 1 / (y^2 - 1) = 0

7.  For the equation of #4, if we are given the initial condition y(1) = 2, what is the largest region of the plane which contains the corresponding point?

8.  For the equation of #5, if we are given the initial condition y(-1) = 2, what is the largest region of the plane which contains the corresponding point?

9.  For the equation of #6, if we are given the initial condition y(0) = 1, what is the largest region of the plane which contains the corresponding point?

3.2

Find at least an implicit solution to each equation.  When possible, find an explicit solution and determine the t interval on which that solution exists:

1.  dy/dt = 1 / y^4, y(1) = 4

2.  y ' + t y ^2 = 0, y(0) = 1.

3.  y ' = 1 + y^2, y(pi/3) = sqrt(3).

4.  y ' = e^(y - 2 t), y(0) = 1.

5.  y ' + e^t sin^2(y) = 0, y(0) = pi/6.

3.3. 

Solve the following:

1.  ( t^2 e^(y t^2) - sin(y) ) dy + 2 y t e^(y t^2) dt = 0

2.  y ' = 2 t y sqrt(y) / (3/2 t^2 sqrt(y) + 1 / y^(3/2) ), y(

3.  (3 y^2 + t^3) y ' + 3 t^2 y = 0, y(1) = 3.

4.  (t^2 e^(t^2 y) + 2 y) dy + 2 t y  e^(t^2 y) dt = 0

5.  If N(t, y) dt + (y^2 - 3 t y) dy = 0 is exact, then what is the function N(t, y)?

3.4.

1.  Solve the equation y ' = 2 t y ( 1 - y), with y(0) = -1, as a Bernoulli equation.

2.  Solve the equation y ' - y = t y^(1/3), y(0) = -9 as a Bernoulli equation.

3.  Solve the equation y ' = - (y + 1) + t ( y + 1)^(-2) as a Bernoulli equation.

3.5.

1.  The population of fish in a pond is initially 4000.  With P measured in months, the population changes according to the equation

dP/dt = 0.05 P * (1 - 0.25 P).

• What is the equilibrium value for this population?
• How long will it take the population to reach 95% of its equilibrium value?

2.  Solve the equation dPdt = r * ( 1 - P / P_c) P + M with r = 1, P_c = 1, P_0 = 1 and M = -1/4.

3.  Solve dP/dt = k ( N - P) * P with P(0) = 100 000 assuming that P is the number of people, out of a population of 500 000, with a disease. Assume that k is not constant, as in the standard logistic model, but that k = 2 e^(-t) - 1. Plot your solution curve and estimate the maximum value of P, and also that value of t when P = 50 000. Interpret all your results in terms of the given situation.

3.6. 

1.  The drag force on an object of mass m is proportional to its velocity.  How long will it take the object to reach 90% of its terminal velocity?  Does the answer depend on the mass of the object or on the proportionality constant?

2.  A 1500 kg car is to be slowed by a parachute from 100 meters / second to 20 meters / second in 5 seconds. Assume a drag force proportional to speed, with proportionality constant k. What is the value of k, and how far will the car travel while being slowed?

3.  A vertical projectile of mass m has initial velocity v_0 and drag force of magnitude k v. How long after being fired will it reach its maximum height? 

If the projectile has mass .12 grams and reaches its maximum height after 2.5 seconds, then what is the value of k?

Repeat on the assumption that the drag force is of magnitude k v^2.

4.  A 82 kg skydiver falls for 10 seconds, subject to gravitational forces and air resistance, then opens his chute. He reaches the ground 3 seconds later. Assume air resistance is proportional to speed, and assume that with this chute a 100 kg individual would reach a terminal velocity of 5 m / s.

At what altitude was the parachute opened?

3.7.

1. Solve the equation m dv/dt = - k v / (1 + y), where y is the position of an object as a function of t and v is velocity as a function of t.

Does this object come to rest? If so, wow far does the object travel before coming to rest?

2. A vertical projectile has initial velocity v_0, and experiences drag force k v^2 in the direction opposite its motion. To what maximum height does the projectile rise?

If the initial velocity is 80 m/s and the projectile, whose mass is .12 grams, rises to a height of 40 meters (estimated quantities for a plastic BB), what is the value of k?

3. Mass m accelerates from velocity v_1 to velocity v_2, while constant power is exerted by the net force. At any instant power = force * velocity (physics explanation: power = dw / dt, the rate at which work is being done; w = F * dx so dw/dt = F * dx/dt = F * v).

How far does the mass travel as it accelerates?

4. What will be the impact velocity of an object which falls to the surface of the Earth from a great height h? Assume that the gravitational force is - G M m / r^2. Neglect air resistance.

Now assume that at height h_atm the object encounters air resistance proportional to the square of its velocity (this is a bit unrealistic because air density changes very significantly with altitude). How long will it take to come to within 50% of its terminal velocity?

A what rate is its kinetic energy therefore changing (the changing kinetic energy will be converted to heat)?

3.8.

1.  Solve the equation x ' = - x + t with x(0) = 0.

Write the expression x_(k + 1) = x_k + h f (t_k, x_k) for h = .01.

Find x_k for k = 0, 1, 2, 3.

Using your original solution for the equation, compare your values of x_k with the values given by the accurate solution.

2.  Euler's method applied to the equation x ' = alpha t + beta, x(t_0) = x_0, yields x values -1, -.8, -.64 and -.51 at respective t values 0, .1, .2, .3. Find the values of alpha, beta, t_0 and x_0.

3.  For each of the following situations, will Euler's method overestimate or underestimate the values of the solution to an equation:

• The solution curve is known to be increasing and concave up.

• The solution curve is known to be increasing and concave down.

• The solution curve is known to be decreasing and concave up.

• The solution curve is known to be decreasing and concave down.

4.  y ' = y^(3/2) with y(0) = 1.

Solve the equation.

Perform Euler's Method to approximate the values of the solution on the t interval [0, 1.6] with step size h = .2.

Compare the values you get with the values given by your solution to the equation.

This could be done by hand, but it would take awhile and the probability of an error would be relatively high. A spreadsheet is recommended.

4.1, 4.2.

1.  A cylinder floating vertically in the water has radius 50 cm, height 100 cm and uniform density 700 kg / m^3. It is raised 10 cm from its equilibrium position and released. Set up and solve a differential which describes its position as a function of clock time.

The same cylinder, originally stationary in its equilibrium position, is struck from above, hard enough to cause its top to come just to but not below the level of the water. Solve the differential equation for its motion with this condition, and use a particular solution to determine its velocity just after being struck.

2.  For each of the equations and initial conditions below, find the largest t interval on which a solution is known to exist:

• y '' + cos(t) y ' + t y = tan(t), y(pi) = 1, y ' (pi) = 0.

• t y '' + tan(t) / (t^2 - 16) y ' + 5 y = 0, y(1) = 1, y ' (1) = -1.

3.  Decide whether the solution of each of the following equations is increasing or decreasing, and whether each is concave up or concave down in the vicinity of the given initial point:

• y '' + y = - 2 t, y(0) = 1, y ' (0) = -1

• y '' + y = - 2 t, y(0) = 1, y ' (0) = -1

• y '' - y = t^2, y(0) = 1, y ' (0) = 1

• y '' - y = - 2 cos(t), y (0) = 1, y ' (0) = 1.

4.3.

1.  Decide whether y_1 = 3 e^t, y_2 = e^(t + 3) are solutions to the equation y '' - y = 0. If so determine whether the two solutions are linearly independent. If the solutions are linearly independent then find the general solution, as well as a particular solution for which y (-1) = 1 and y ' (-1) = 0.

2.  Decide whether y_1 = e^(-t) and y_2 = 2 e^(1 - t) are solutions to the equation y '' + 2 y ' + y = 0. If so determine whether the two solutions are linearly independent. If the solutions are linearly independent then find the general solution, as well as a particular solution for which y (0) = 1 and y ' (0) = 0.

3.  Suppose y_1 and y_2 are solutions to the equation

y '' + alpha y ' + beta y = 0

and that y_1 = e^(2 t). Suppose also that the Wronskian is e^(-t).

What are the values of alpha and beta?

4.  Suppose y1 and y2 are solutions to y '' + 2 t y ' + t^2 y = 0. If y1(3) = 0, y1 ' (3) = 0, y2(3) = 1 and y2 ' (3) = 2, can you say whether {y1, y2} is a fundamental set? If so, is it or isn't it?

5.  Are y1 = - e^(-2 t) sin(t) and y2 = 4 e^(-2 t) cos(t) solutions to the equation y '' + 4 y ' + 5 y = 0?

What are the initial conditions at t = 0?

Is {y1, y2} a fundamental set?

6.  y1_bar = 2 y1 - 2 y2 and y2_bar = y1 - y2. If {y_1, y_2} is a fundamental set, is {y1_bar, y2_bar} a fundamental set?

7.  Is {e^(2t), 2 e^(-2t), sinh (2t) } a fundamental set on the interval (-infinity, infinity)?

4.4. 

1.  Find the general solution to

y '' - 5 y ' + 4 y = 0

and the unique solution for the initial conditions y (0) = 1, y ' (0) = 2.

How does the solution behave as t -> infinity, and as t -> -infinity>?

2.  Find the general solution to

y '' - 6 y ' + 8 y = 0

and the unique solution for the initial conditions y (1) = 1, y ' (1) = -3.

How does the solution behave as t -> infinity, and as t -> -infinity>?

3.  Solve the equation

m ( r '' - Omega^2 r) = - k r ' for r(0) = 0, r ' (0) = v_0.

Omega is the angular velocity of a centrifuge, m is the mass of a particle and k is drag force constant. Physics students will recognize that m r Omega^2 is the centripetal force required to keep an object of mass m moving in a circle of radius r at angular velocity Omega.

The equation models the motion of a particle at the axis which is given initial radial velocity v_0.

The mass m of a particle is proportional to its volume, while the drag constant is proportional to its cross-sectional area. Assuming all particles are geometrically similar (and most likely spherical, though this is not necessary as long as they are geometrically similar, but for the sake of an accurate experiment spheres would be preferable), how then does k / m change as the diameter of particles increases?

If Omega = pi radians / second and v_0 = 0.5 cm / second, with k / m = 2 s^-1, find the value of r at t = 3 seconds.

4.5, 4.6

1. Solve the equation

16 y '' + 16 y ' + 4 y = 0,

with y(4) = 4 e^-2 and y ' (4) = -1/2 e^-2.

2. Solve the equation

8 y '' + 4 sqrt(2) y ' + y = 0, y(0) = sqrt(2), y ' (0) = 3

3. Solve the equation

y '' - 2 cot(t) y ' + (1 + 2 cot^2 t) y = 0,

which has known solution y_1(t) = sin(t)

You will use reduction of order, find intervals of definition and interval(s) where the Wronskian is continuous and nonzero. See your text
for a more complete statement of a similar problem.

4.7.

1.  A 30 kg mass stretches a spring 50 mm beyond its unloaded position. The spring is pulled down to a position 130 mm below its unloaded position and released.

Write and solve the differential equation for its motion.


2.  The graph below represents position vs. clock time for a mass m oscillating on a spring with force constant k. The position function is y = A cos(omega t - theta_0).

Find theta_0, omega and A.

Give the initial conditions on the y and y '.

Determine the mass and the force constant in terms of theta_0, omega, A and k.

Describe how you would achieve these initial conditions, given the appropriate mass and spring in front of you.

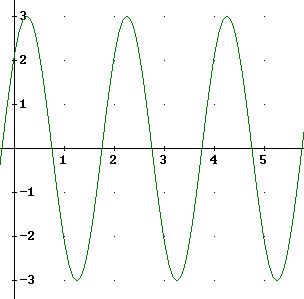
3.  Repeating the first problem:

'A 30 kg mass stretches a spring 50 mm beyond its unloaded position. The spring is pulled down to a position 130 mm below its unloaded position and released.'

Suppose that instead of simply releasing it from its 130 mm position, you deliver a sharp blow to get it moving at downward at 140 mm / second.

What initial conditions apply to this situation?

Apply the initial conditions to the general solution of the differential equation, and give the resulting function


4.  The 10-kg mass at its equilibrium position in a critically-damped spring-and-dashpot system is given a 2 meter / sec upward initial velocity, and attains a maximum displacement of 25 inches from equilibrium. What are the values of the drag force constant gamma and the spring constant k?

5.  The motion of a system is governed by the equation m y '' + gamma y ' + k y = 0, with y(0) = 0 and y ' (0) = v_0.

Give the solutions which correspond to the critically damped, overdamped and underdamped cases.

Show that as gamma approaches 2 sqrt(k * m) from above, the solution to the underdamped case approaches the solution to the critically damped case.

Show that as gamma approaches 2 sqrt(k * m) from below, the solution to the overdamped case approaches the solution to the critically damped case.

4.8, 4.9.

1. Find the general solution of the equation

y '' + y = e^t cos(t).

2. Find the general solution of the equation

y '' + y ' = t^2

3. Find the general solution of the equation

y '' + y ' = sin(t).

4. Give the expected form of the particular solution to the given equation, but do not actually solve for the constants:

y '' - 2 y ' + 3 y = 2 e^-t cos(t) + t^2 + t e^(3 t)

5. Give the expected form of the particular solution to the given equation, but do not actually solve for the constants:

y '' + 4 y = 2 sin(t) + cosh(t) + cosh^2(t).

6. The equation

y '' + alpha y ' + beta y = t^2 + cos(t)

has complementary solution y_C = c_1 cos(t) + c_2 sin(t) (i.e., this is the solution to the homogeneous equation).

Find alpha and beta, and solve the equation.

7. Consider the equation

y '' - y = e^(`i * 2 t),

where `i = sqrt(-1).

Using trial solution

y_P = A e^(i * 2 t)

find the value of A, which is in general a complex number (though in some cases the real or imaginary part of A might be zero)

Show that the real and imaginary parts of the resulting function y_P are, respectively, solutions to the real and imaginary parts of the original equation.

4.10

1.  Using variation of parameters, solve the equation

y '' + y = tan(t), -pi/2 < t < pi

2.  Using variation of parameters, solve the equation

y '' + 64 y = sec^3 ( 8 t ).

4.11.

1.  A 5 kg mass stretches a spring 12 cm beyond its original rest position.

A driving force F(t) = 10 N * cos((5 s^-1) * t) begins at t = 0, where the downward direction is regarded as positive.

Write down and solve the appropriate differential equation, obtaining the position function for the motion of the mass.

Plot your solution, and find the maximum distance of the mass from its equilibrium position.

2.  The motion of a mass is governed by the equation

m y '' + 2 gamma y ' + omega_0^2 y = F(t),

where y is position with respect to equilibrium,  The object is originally at rest at its equilibrium position.

Suppose that m = 3 kg, gamma = 12 kg / s, k = 100 N / m and F(t) = 35 N * e^(- 0.5 t s^-1).

Solve the equation for the function y(t).

What is the long-term behavior of this system?

3.  Solve the equation

y '' + 2 delta y ' + omega_1^2 y = F sin( omega_2 * t),

where the mass is considered to be initially at rest at its equilibrium position.

Assume that omega_1^2 is greater than delta, so that the discriminant of the characteristic equation is negative.

Give an outline of your work. A very similar problem was set up and partially solved in class on 110309, and your text gives the solution but not the steps.

Find the limiting function as omega_2 approaches omega_1, and discuss what this means in terms of a real system.

Find the limiting function as delta approaches 0, and discuss what this means in terms of a real system.

4.  An LC circuit with L = 2 Henry and C = 3 microFarads is driven by voltage V_source(t) = 12 t e^(-0.4 t).

Write and solve the differential equation for the system.

Interpret your result.

6.1.  Find the values of t for which the matrix

[ t , t + 1; t-1, t + 1]

pictured as:

is invertible.

2.  Find the limit as t -> 0 of the matrix

[ 2 sin(t) / t,3 / (t^2 - 1),  4 t tan(t); csc(t), e^(3 t), t^3 / (t^2 - 1) ]

pictured as

3.  Find A ' (t) and A ''(t), where the derivatives are with respect to t and the matrix is

A = [-t, cos(t); t / (t + 1), 5 t^3]

pictured as

4.  Write the system of equations

y_1 ' = cos(t) y_1 + t y_2 - cot(t)

y_2 ' = tan(t) y _1 + t^2 y_2 + 8

in the form

y ' = P(t) y + g(t),

where P(t) is a 2 x 2 matrix and y and g(t) are 2 x 1 column vectors.

5.  If

A '' = [t, 0; 0, 1]

with

A(0) = [ 1, 1; -2, 1]

A(1) = [-1, 2; -2, 3 ]

then what is the matrix A(t)?

6.  Find the matrix A(t), defined by

A(t) = integral( C(s) ds, s from 0 to t),

where

[4s, s e^(s^2); sin(3 pi s), cos(3 pi s) ].

6.2

1.  What is the largest interval over which the solution to the system

(t +1) y_1 ' = t y_1 + 2 y_2

(t - 3) y_2 ' = -2 y_1 + 3 y_2

with initial conditions

y_1(1) = 0

y_2(1) = 2

is defined?

2.  The equation

y ' = [y_1 + y_2; y_2 - 2 y_3; -3 y_1 + 2 y_3 + e^(-2 t) ]

with initial condition

y(0) = [-2, 1, 4]

represents a higher-order equation of form

y[n] + a_(n-1) * y[n-1] + ... + a^2 y '' + a_1 y ' + a_0 y = g(t).

(y[n], for example, represents the nth derivative of y; a_(n-1) is understood as a with subscript n - 1).

What is the higher-order equation?

6.3.

1.  Verify Abel's Theorem on the interval (-infinity, infinity) for

y ' = [ 6, 5; -7, -6] * y

whose solutions are

y_1 = [ 5 e^-t; -7 e^-t ]

y_2 = [ e^t; - e^t ]

with t_0 = -1

2.  y ' = A y, with solutions

y_1 = [5; 1]

y_2 = [2 e^(3 t), e^(3 t) ]

Verify that this constitutes a fundamental set.

Find Tr(A).

Show that

psi(t) = [y_1, y_2]

satisfies

psi ' = A * psi

Find A by finding psi ' * psi^-1

Is the result consistent with your result for the trace of A?

Sections 6.4, 6.5

1.  Determine whether the set of solutions {y_1, y_2, y_3} is linearly independent, where

y_1 = [ e^t; 1]

y_2 = [ e^(-t); 1]

y_3 = [ sinh(t); 0]

2.  Determine whether the set of solutions {y_1, y_2, y_3} is linearly independent, where

y_1 = [ 1, sin^2(t), 0]

y_2 = [ 0, 2 - 2 cos^2(t), -2]

y_3 = [ 1, 0, 1]

3. Determine whether there is a matrix P(t) such that

y_1 = [ t^2, 0 ]

y_2 = [ 2t, 1 ]

is a fundamental set of solutions to the equation

y ' = P(t) y.

If so, find such a matrix P(t).

Hint:  The matrix psi(t) = [y_1, y_2 ] = [ t^2, 2 t; 0, 1 ] would need to satisfy psi ' (t) = P(t) psi(t).

In standard notation we could write this as follows:

satisfies

4.  If the matrix psi(t) = [y_1, y_2] = [e^t, e^(-t); e^t, - e^(-t)]:

What are the vector functions y_1 and y_2?

Write out the system of two differential equations represented by the equation y ' = P(t) y with P(t) = [0, 1; 1, 0].

Show that y_1 and y_2 are both solutions of the equation y ' = P(t) y with P(t) = [0, 1; 1, 0].

Show that { y_1 , y_2} is a fundamental set for this equation.

Show that the matrix psi(t) is a solution of the matrix equation psi ' = P(t) psi.

Show that the matrix psi(t) is a fundamental matrix for the linear system of equations.

Let psi_hat(t) = [ 2 e^t - e^(-t), e^t + 3 e^(-t); 2 e^t + e^(-t), e^t - 3e^(-t) ].

Find a constant matrix C such that psi_hat(t) = psi(t) * C.

Based on your matrix C, is psi_hat(t) a solution matrix for the system?

Based on your matrix C, is psi_hat(t) a fundamental matrix for the system?

5.  Given the system

y ' = [ 1, 1; 0, -2 ] y

verify that

psi(t) = [ e^t, e^(-2 t); 0, e^(-2 t) ]

is a fundamental matrix for the system.

Find a matrix C such that

psi_hat(t) = psi(t) * C

is a solution matrix satisfying initial condition psi_hat(0) = I, where I is the identity matrix.

6.  Find the solutions to y ' = A y when

A = [ 5, 3; -4, -3 ]

and

y(1) = [2; 0].

Section 6.6

1.  Find the eigenvalues of the matrix [3, 1; -2, 1] and find the corresponding eigenvectors.

2.  Suppose that i + 1 is an eigenvalue of a matrix A and [-1 + i, i ] is a corresponding eigenvector.  Find a fundamental set of real solutions to the equation y ' = A y.

3.  Solve the equation

y ' = [0, -9; 1, 0] y

with initial condition

y(0) = [6, 2].

4.  Find all values of mu such that any fundamental set [ y_1, y_2 ] of the system

y ' = [1, 3; mu, -2] y

have the property that the limit of the expression (y_1(t))^2 + (y_2(t))^2, as t -< infinity, is zero.

5.  A particle moves in an unspecified force field in such a way that its position vector r(t) = x(t) i + y(t) j and the corresponding velocity vector v(t) = r ' (t) satisfy the equation

v ' = 2 k X v

Write this condition as a system

v ' = A v,

with v = [v_x; v_y].

If the particle starts at position r(0) = 2 i + j, v(0) = i + 2 j, find its position at t = 3 pi / 2.

6.7, 6.8

6.10

1.  Diagonalize the matrix [2, 3; 2, 3].

2.  Find the algebraic and geometric multiplicity of each eigenvalue and, if possible, diagonalize the matrix

[ 5, -1, 1; 14, -3, 6; 5, -2, 5 ].

The characteristic equation of this matrix is (lambda - 2)^2 ( lambda -3).

3.  Solve the system

y  ' = [ -4, -6; 3, 5 ] y + [e^(2 t) - 2 e^t; -e^(2 t) + e^t]

4.  Solve

x '' = [ 6, 7; -15, -16] x

6.11.

1.  Find the propagator matrix Phi(t) = e^(t A) for the system

y ' = [5, -4; 5, -4] y

and use to find y(3) given that y(1) == [ 1, 0].

2.  Use a propagator matrix to find y(1), given  y ( 0 ) = [1; 1; 0], for the system

y ' = [ 1, 1, 1; 0, 2, 1; 0, 0, -1 ] y.

3.  Given the solution matrix

psi(t) = [t, t^2; 1, 2 t]

find the propagator matrix phi(t, s), t > 0, s > 0.

Is the propagator matrix a function of t - s?

Find y(3) given that y(1) = [1, -1].

4.  Suppose that T^-1 A T = [lambda_1, 0; 0, lambda_2].

Let p(A) be the matrix polynomial 2 A^3 - A + 3 I.

Find the matrix B such that p(A) = T B T^-1.

5.  Let A be invertible and diagonalizable, and let D = T^-1 A T be the matrix as diagonalized by a similarity transform.

Show that D is invertible.

Show that A^-1 is diagonalizable by the same similarity transform that diagonalizes A (i.e., show that D^-1 = T^-1 A^-1 T).

6.  Let A be a diagonalizable 2 x 2 matrix with

lambda_1 = 1/4, x_1 = [2, 5]

and

lambda_2 = 1/2, x_2 = [1, 3].

Find cos(pi A) and sin(pi A).

7.  Let A be a diagonalizable 2 x 2 matrix with

lambda_1 = 1/4, x_1 = [2, 5]

and

lambda_2 = 1/2, x_2 = [1, 3].

Solve the equation

y '' + y ' + A y = 0.

7.1, 7.2

1.  Using the definition of the Laplace transform, find the Laplace transform of f(t) = t e^(t sqrt(t)).

2.  Using the definition of the Laplace transform, find the Laplace transform of the function f(t) defined by f(t) = 0, 0 <= 1 < 1; f(t) = t - 1, 1 <= t.

3.  Using the definition of the Laplace transform, find the Laplace transform of f(t) = cos(omega t).

4.  Using the definition of the Laplace transform, find the Laplace transform of f(t) = e^(3 t) sin(t).

7.3

1.  Using, if necessary, the table in your text, find the Laplace transform of e^(3 t - 3) * h(t - 1), where h(t) is the Heaviside function.

2.  Using, if necessary, the table in your text, find the Laplace transform of e^(2 t) cos(3 t).

3.  Using, if necessary, the table in your text, find the inverse Laplace transform of 10 / (s^2 + 25) + 4 / (s - 3).

4.  Using, if necessary, the table in your text, find the inverse Laplace transform of e^(-2 s) / (s - 9).

5.  Using, if necessary, the table in your text, find the inverse Laplace transform of 1 / (s + 1)^3

6.  Using, if necessary, the table in your text, find the inverse Laplace transform of (2 s - 3) / (s^2 - 3 s + 2).

7.4

1.  Use Laplace transforms to solve the equation y ' + 2 y = 4 t, with initial condition y(0) = 3.  Verify your solution.

2.  Let f(t) = sin(t) for 0 <= t < pi, f(t) = 0 for pi <= t < 2 pi, with f(t + 2 pi) = f(t).

Graph this periodic function and find its Laplace transform.

3.  Find the function whose Laplace transform is (s^2 - s) / s^3 + e^(-s) / (s ( 1 - e^(-s) ).