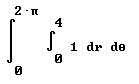
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.
It is assumed you are familiar with polar coordinates from prerequisite courses. If necessary you can refresh yourself by using some lecture notes from Precalculus II at http://vhcc2.vhcc.edu/pc2fall9/lectures/990311/class_notes.htm For further refreshers you can check any of a variety of online sources. Khan Academy is always recommended.
Question: `q001. Give a simple description of the polar-coordinate region defined by
0 <= r <= 4
0 <= theta <= 2 pi.
Your solution:
Confidence rating:
Given Solution: Since r = 4 is included in the given description, as are all angles from 0 to 2 pi, the points (r, theta) within the given region include the points (4, theta) for theta = 0 to 2 pi. These points all lie at distance 4 from the pole, so they lie on a circle of radius 4 centered at the pole. Any point on the circle can be described by the ordered pair of polar coordinates (4, theta) for the appropriate angle theta between 0 and 2 pi. Since all angles from 0 to 2 pi are included in the description of the region, the region described does include all such points. It follows that the entire circle of radius 4, centered at the origin, is part of the described region.
The same can be said for any radius r < 4. So the described region includes all circles about the pole whose radius is less than or equal to 4.
Any point which lies at a distance less than or equal to 4 from the pole lies on one of these circles. It follows that the described region consists of the entire disk of radius 4, centered at the pole.
A more succinct argument:
Every point within the disk of radius 4 centered at the pole lies at a distance <= 4 from the pole, and the line from the pole to the point makes an angle between 0 and 2 pi with the polar axis. So every point on the disk can be described by polar coordinates (r, theta) with r <= 4 and 0 <= theta < 2 pi.
Furthermore, any point outside this disk lies at distance greater than 4 from the pole, so cannot be included in our description, which requires that r be less than or equal to 4.
Thus a point (r, theta) fits our description if, and only if, it lies within the said disk.
Self-critique (if necessary):
Self-critique rating:
Question: `q002. We might expect that, to get the area of the disk of the preceding problem, we could just integrate f(r, theta) = 1 from r = 0 to 4, and from theta = 0 to 2 pi.
Verify that this is not in fact the case by evaluating
integral( integral( 1 dr, r from 0 to 4) dTheta, theta from 0 to 2 pi).
In standard notation this integral is
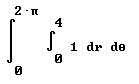
Your solution:
Confidence rating:
Given Solution: The integral is easily calculated, and its value is 8 pi.
However the area of a circle of radius 4 is pi r^2 = pi * 4^2 = 16 pi.
So clearly the said integral doesn't give us the correct area.
The next few problems will show us why.
Self-critique (if necessary):
Self-critique rating:
Question: `q003. To integrate to find the area of a region with respect to r and theta, we begin by partitioning our r interval and our theta interval. An r interval partitions the region into concentric circles, while a theta interval partitions it into wedge-shaped regions that become larger as we move away from the pole. The figures below show the circles we get from partitioning the interval 0 <= r <= 4 into 20 equal intervals, the 'wedges' we get from partitioning the interval 0 <= theta <= 2 pi into 20 equal intervals, and the two regions superimposed.
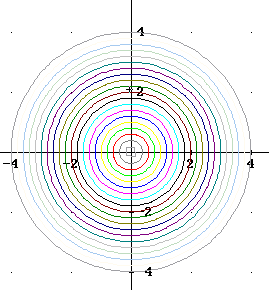
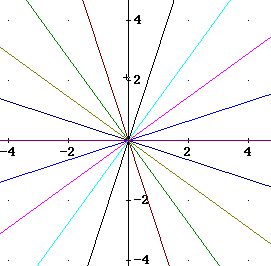
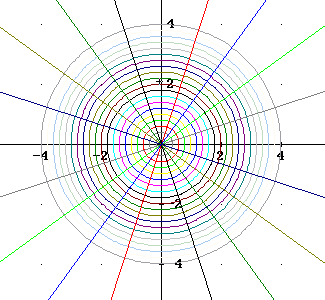
The region inside the circle is subdivided into 400 smaller subregions. The r interval for every region is the same, and the same is so for the theta intervals. However the areas of the various subregions are not the same.
Explain why this is so.
Your solution:
Confidence rating:
Given Solution: The areas of the various subregions get progressively larger as we move further from the pole. This is because of the wedge shape of the regions defined by the theta intervals. Those intervals get progressively further apart as we move further from the pole. The r intervals stay the same, so the subregions have the same width in the r direction regardless of where they are, but they have greater and greater lengths, and therefore greater and greater areas, in the direction of increasing theta.
Self-critique (if necessary):
Self-critique rating:
Question: `q004. What is wrong with saying that the area of an interval is `dr * `dTheta?
Your solution:
Confidence rating:
Given Solution: There are two things wrong with this.
For one, `dr * `dTheta is the same for every region, and it is clear that the regions do not all have the same area.
For another, `dr * `dTheta has units of length * angle, so it can't be an area. An area has units of length * length (e.g., meters^2, or cm^2, or ft^2, or miles^2, or km^2).
Self-critique (if necessary):
Self-critique rating:
Question:
`q005. Dividing the interval 0 <= r <= 4 into 20 equal subintervals gives us r interval 0.2. Dividing the interval 0 <= theta < 2 pi into 20 equal intervals gives us theta interval pi/10.
Give your best estimate of the area of the largest subregions on the graph, and the area of the smallest.
Your solution:
Confidence rating:
Given Solution: The largest subregions occur in the outermost 'ring' of the graph, where r varies from 3.8 to 4.
The 'length' of one of those regions along the arc of the outermost circle, by the definition of the radian (which you should review and understand if you don't already) is therefore 4 * pi/10 = 2 pi / 5, which is approximately 1.26. Of course the 'length' along the inner boundary of the region, along the circle of radius 3.8, is a bit smaller, closer to 1.20. We could compromise and say that the arc is about 1.23.
The region isn't exactly a rectangle, but our angle `dTheta is small enough that there is little curvature in the region. So we won't be too far off if we assume the region to be a rectangle 1.23 units long and .20 units wide. Its area would be roughly .25.
The smallest intervals are very nearly triangular in shape, forming a small 'wedge' with its vertex at the origin. This 'wedge' is bounded by the circle of radius .20, so its vertex angle of pi / 10 dictates that the arc of the circle bounding this wedge is pi / 10 * .20 = pi / 50, or about .061. There is some small curvature along this arc, but it is small enough that we can regard our wedge-shaped region are a triangle with altitude 0.20 and base 0.61. The area of this region is therefore about 0.20 * 0.61 = 0.12.
The main point here is that, as long as `dTheta is small enough the relevant arc of the circle can be regarded as a straight line and the region as a rectangle (or for a region adjacent to the pole as a triangle). You should sketch this situation and convince yourself that, as long as `dTheta and `dr are small enough, this gives us a good approximation of the area of a subregion.
Self-critique (if necessary):
Self-critique rating:
Question:
`q006. Now let's imagine that `dr and `dTheta are much smaller than pictured in the circle, so that they are plenty small to regard as rectangles. What would be the dimensions of a `dr by `dTheta region that contains sample point (r_hat, theta_hat)?
Your solution:
Confidence rating:
Given Solution: The arc of the circle r = r_hat that lies within the region would be the product of the radius of that circle and the angle `dTheta. So the arc would have length r_hat * `dTheta.
Since `dr is small, there will be little appreciable difference between this arc and any other such arc that lies within the region. So we can take this as the length of our nearly-rectangular region.
The width of the region will be `dr.
So our region has area very close to
area of subregion = length * width = r_hat `dTheta * `dr.
Self-critique (if necessary):
Self-critique rating:
Question: `q007. For the circle of radius 4, if the circle represents a laminar region whose density at the point (r, theta) is 1 + r, then:
What are the maximum and minimum densities in the region and where do they occur?
Where in the circle is the density 4?
In what region of the circle is the density between 2.5 and 3.5?
What is the mass of the laminar region?
Your solution:
Confidence rating:
Given Solution:
The maximum value of the expression 1 + r within the circular region occurs when r takes its greatest value within the region. Since the circle is described by 0 <= r <= 4, the maximum value of r is 4, so the maximum value of the density 1 + r is 1 + 4 = 5. This density occurs at the very outer edge of the circle.
The minimum value of r is 0, which occurs at the very center of the circle, so the minimum density occurs at this point and has value 1 + 0 = 1.
The value of the density 1 + r is 2.5 when 1 + r = 2.5, which occurs when r = 1.5. This occurs on the circle of radius 1.5.
Similarly it is easy to see that the density is 3.5 on the circle of radius 2.5, and also that the density is between 2.5 and 3.5 for the ring between r = 1.5 and r = 2.5.
The mass of a given `dr by `dTheta area increment with sample point (r_hat, theta_hat) is found by multiplying the density at the sample point by the area of the region. The density at the sample point is 1 + r_hat and, as we have seen, the area of the region is r_hat `dTheta * `dr, so the mass of the area increment would be
`dm = density * area = (1 + r_hat) * r_hat `dTheta * `dr.
The Riemann sum over all such areas approaches the integral
integral ( integral ( (1 + r) * r `dr, r from 0 to 4) `dTheta, theta from 0 to 2 pi)
or in standard notation
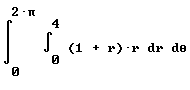
The integration is easily performed and the result is 176 pi / 3, or about 184.
Self-critique (if necessary):
Self-critique rating:
Question:
`q008. What portion of the mass of the circular region in the preceding problem lies in the region where the density is between 2.5 and 3.5?
What portion of the mass of the circular region lies at distance greater than 3 from the center?
For a non-required challenge problem, can you figure out the radius of the concentric circle that splits the mass of the region in half? Hint: The answer is r = (32 - sqrt(65535)/8)^(1/3) + (sqrt(65535)/8 + 32)^(1/3) - 1/2, which is approximately 3.5625. All you need to do is show how to get this. Your instructor would in fact be favorably impressed if you could get the equation - pi ( 2 r^3 + 3 r^2 - 176) / 3 = 176 pi / 3, whose solution for r matches the solution r = (32 - sqrt(65535)/8)^(1/3) + (sqrt(65535)/8 + 32)^(1/3) - 1/2. Note: It looks a lot worse than it is.
Your solution:
Confidence rating:
Given Solution:
The region where density is between 2.5 and 3.5 was seen in the preceding to lie between the circles r = 1.5 and r = 2.5. The typical region between these circles is identical to that used in the preceding problem to find the mass integral, with only the restriction that whereas r_hat was previously restricted only to the interval 0 <= r_hat <= 4, it is now restricted to the interval 1.5 <= r_hat <= 2.5.
The only difference this makes is that r_hat values in our Riemann sum have the same restriction, and this leads to the limits 1.5 and 2.5 on our r integral.
Our integral for the mass within this region is therefore
integral ( integral ( (1 + r) * r `dr, r from 1.5 to 2.5) `dTheta, theta from 0 to 2 pi)
The integration is again straightforward, and we get result 73 pi / 6. We conclude that the mass of the circular ring between r = 1.5 and r = 2.5 is (73 pi / 6) / (176 pi / 3) = (73 * 3) / (176 * 6) = 73 / 352 = .207, approximately.
So to the nearest percent, the mass in this ring is 21% of the total mass.
The mass lying more than 3 units of distance from the center can be seen by similar reasoning to be
integral ( integral ( (1 + r) * r `dr, r from 3 to 4) `dTheta, theta from 0 to 2 pi) = 95 pi / 3, which is over half the mass of the entire region.
Self-critique (if necessary):
Self-critique rating:
Question:
`q009. Set up and evaluate the integral that yields the area bounded by the spiral r = theta + 1 in the first quadrant.
Your solution:
Confidence rating:
Given Solution:
The first quadrant runs from theta = 0 to theta = pi/2. Between these two values of theta the coordinate r runs from r = 0 + 1 = 1, at theta = 0, to r = pi/2 + 1 (approximately 2.57) at theta = pi/2.
The inequalities that define this regions would be
0 <= theta <= pi/2
0 <= r <= theta + 1.
The area increment r dr dTheta will be integrated over this region, yielding integral
integral(integral(r dr, r from 0 to theta + 1) dTheta, theta from 0 to pi/2) = pi ( pi^2 + 6 pi + 12 ) / 48, or approximately 2.66.
You should have a reasonable sketch of this region, and your estimate of its area should be consistent with this result.
Self-critique (if necessary):
Self-critique rating:
Question:
`q010. The polar-coordinates point (r, theta) lies at distance r from the pole, along a radial line that makes angle theta with the polar axis.
If the polar axis coincides with the positive x axis of a rectangular coordinate system, then what are the x and y coordinates of that point?
Your solution:
Confidence rating:
Given Solution:
The point (r, theta) lies on a circle of radius r centered at the pole, on the radial line making angle theta with the pole. The pole coincides with the origin of the xy system, and the polar axis with the positive x axis, so the point lies on a circle centered at the origin of this system on the radial line making angle theta with the positive x axis.
By the circular definition of the trigonometric functions, the point has rectangular coordinates ( r cos(theta), r sin(theta) ).
Summarizing:
If r and theta are the polar coordinates of a point, then x = r cos(theta) and y = r sin(theta) are its rectangular coordinates.
Self-critique (if necessary):
Self-critique rating:
Question: `q011. What are the polar coordinates of the point (x, y) in a rectangular coordinate system?
Your solution:
Confidence rating:
Given Solution: The point (x, y) lies at distance sqrt(x^2 + y^2) from the origin, and a radial line from the origin through (x, y) makes angle arcTan(y / x), or if the x coordinate is negative arcTan(y / x) + pi radians, with the positive x axis. If the pole of the polar coordinate system coincides with the origin of the rectangular system, and the polar axis with the positive x axis, then the polar coordinates of the point are r = sqrt(x^2 + y^2) and theta = arcTan(y / x), plus pi radians if x < 0.
Summarizing:
The point (x, y) of a rectangular coordinate system corresponds to the point (r, theta) of the polar coordinate system, with r = sqrt(x^2 + y^2) and theta = arcTan(y/x), plus pi radians if x < 0.
Self-critique (if necessary):
Self-critique rating:
Question: `q012. Convert the following equation in rectangular coordinates to a equation in polar coordinates:
x^2 + y^2 + x = y
Your solution:
Confidence rating:
Given Solution:
It should be clear from the Pythagorean Theorem that x^2 + y^2 = r^2.
In any case the definition of r as
r = sqrt(x^2 + y^2)
implies that r^2 = x^2 + y^2.
Also,
x = r cos(theta) and y = r sin(theta).
Our equation therefore becomes
r^2 + r cos(theta) = r sin(theta),
or
r^2 = r (sin(theta) - cos(theta)),
so that
r = sin(theta) - cos(theta).
Self-critique (if necessary):
Self-critique rating:
Question: `q013. Express the equation
r^2 = cos(theta)
in polar coordinates.
Your solution:
Confidence rating:
Given Solution:
r = sqrt(x^2 + y^2) so r^2 = x^2 + y^2.
r cos(theta) = x so
cos(theta) = x / r = x / sqrt(x^2 + y^2).
Thus the equation is
x^2 + y^2 = x / (sqrt(x^2 + y^2) ),
which can be expressed as
(x^2 + y^2) ^(3/2) - x = 0.
We could also solve this equation for y to obtain
y = +-sqrt( x^(2/3) - x^2).
We note that this equation is defined only if x^(2/3) - x^2 >= 0, which is the case if and only if | x | <= 1. This is consistent with the fact that since cos(theta) <= 1, r in our original definition must have a magnitude not exceeding 1, so that | r | <= 1.
Self-critique (if necessary):
Self-critique rating: