If your solution to stated problem does not match the given solution, you should self-critique per instructions at

 

   http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm

.

Your solution, attempt at solution.  If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it.  This response should be given, based on the work you did in completing the assignment, before you look at the given solution.

At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises. 

 

 

 

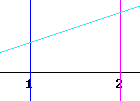
Question:  `q001.  The sloping line in the figure below has slope 0.5. 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

The rise of the segment is 0.5 times its run.  Its run is 1, so its rise is 0.5.

A line segment with a run of 1 and a rise of 0.5 has length sqrt(1^2 + 0.5^2) = sqrt(5) / 2.

The segment makes an angle of arcTan(0.5 / 1) (roughly 27 degrees) with the x axis, so its angle with the y axis is arcTan(1 / 0.5) (roughly 63 degrees).

If theta is the angle of the segment with the x axis, then since the y axis lies perpendicular to the x axis and the normal lies perpendicular to the segment, the angle of its normal with the y axis is equal to theta.  This angle is depicted in the first figure below and is depicted twice in the second figure.

                

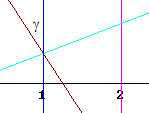
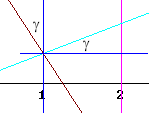
The the figure below contains only one triangle.  The angle gamma is indicated within this triangle, and is equal to the angle of the normal with the vertical (i.e., the y) direction.

It should be clear from basic triangle trigonometry that cos(gamma) is equal to the horizontal leg of this triangle divided the its hypotenuse.

It follows that the hypotenuse of the triangle is equal to the horizontal leg divided by the cosine of gamma.  The horizontal leg being the horizontal distance between x = 1 and x = 2, and the hypotenuse being the length of the sloping segment between x = 1 and x = 2, we conclude that between x = 1 and x = 2

Since sec(gamma) = 1 / cos(gamma), this can also be written

Generalization:

More generally, if `dx is the length of a subinterval partitioning an interval of the x axis, the length `dL of the 'sloping segment' directly 'above' the `dx segment is

`dL = `dx / cos(gamma) = `dL * sec(gamma).

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  `q002.  Imagine a flat pane of glass constrained to rotate about the y axis.  We are interested in how the area of that pane lying directly above the square 1 <= x <= 2, 2 <= y <= 3 is related to the area of the square.

Let's call this square W (we won't call it S, which would seem natural, because we're going to use S for the surface area of whatever lies above our region in the xy plane).

It should be obvious that if the pane is lying flat on the xy plane, then since it is lying right on our square the area of the pane just above our square is equal to the area of our square.

Suppose that with the pane in this position we trace the lines y = 2 and y = 3 on the glass, then rotate the glass pane so that it makes a 45 degree angle with the xy plane.  Since the pane is constrained to rotate about the y axis, the lines we have just drawn will remain perpendicular to that axis.  They will therefore continue to lie in the y = 2 and y = 3 planes, and will therefore continue to lie above the lines y = 2 and y = 3 in the xy plane. 

When we rotate the plane from it position flat on the xy plane to the 45 degree angle, every point on the glass pane, except the points on the y axis, will move closer to the yz plane.  If we continue to rotate the glass pane until it reaches a 90 degree angle with the xy plane, it will in fact lie in the yz plane.

Now, had we drawn the x = 1 and x = 2 lines on the glass when it was flat on the xy plane, upon rotating the pane to the 45 degree position those lines would move closer to the yz plane, and would no longer lie above the x=1 and x=2 lines in the xy plane.  We will not sketch these lines, but let's imagine sketching the lines that now lie directly above the x = 1 and x = 2 lines in the xy plane.

These lines, along with the y = 2 and y = 3 lines, will form a rectangle on our glass pane. 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

The figure below shows a 'side view' of the plane, looking at it from a point far out on the y axis.  The axes shown are the x and z axes.

The lines above x = 1 and x = 2 are vertical lines parallel to the z axis, extending up and out of the xy plane.  The lines directly above x = 1 and x = 2 are separated by the length of the blue line segment.  It is easily seen that the blue segment has length 1 / cos(45 deg) = 1 / (sqrt(2) / 2) = sqrt(2).

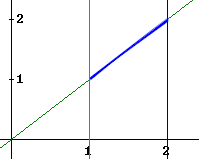
The y = 2 and y = 3 lines on our glass plane (which because of our point of view in the figure above cannot be seen, since since they are seen end-on) are still 1 unit apart, so the rectangle on the glass pane has dimensions 1 by sqrt(2), and area sqrt(2).

The area of the square W in the xy plane is 1, so the area of the rectangle on the pane exceeds that of the square beneath it by the factor sqrt(2).

If the glass pane is at angle gamma, then the length of the 'blue' segment is 1 / cos(gamma) and the area of the rectangle on the glass pane is 1 / cos(gamma) times the area of the square in the xy plane.  That is, the area on the glass pane is increased relative to the area of the square by factor 1 / cos(gamma) = sec(gamma).

In the figure below the angle gamma is indicated between the line segment and the horizontal direction, as well as between the normal to the line segment and the upward vertical direction.

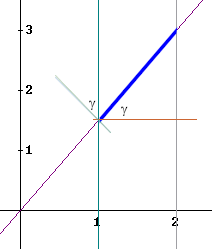
Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  `q003.  If the glass pane is now freed from its attachment to the y axis and permitted to tilt in any manner (as opposed to remaining parallel to the y axis), then its orientation is most easily described by the vector normal to its plane.  You are familiar with the normal vector to the plane from previous work in this course.

Since the pane can be tilted in any manner, the lines above the y = 2 and y = 3 lines in the xy plane can no longer be expected to lie 1 unit apart, and of course the same is true for the lines above the x = 1 and x = 2 lines in the xy plane.

In terms of the x, y and z axes and the unit vectors `i, `j and `k, the factor by which the area of the rectangle lying on the plane directly above our unit square W (which is still in the same position in the xy plane) is still 1 / cos(gamma) = sec(gamma), where gamma is the angle between the normal vector and the vertical `k vector (the unit vector in the z direction).  If the normal vector is parallel to the `k vector, then our glass pane is parallel to the xy plane and the area of the region of our glass pane above the unit square W is 1, identical to the are of that square.  The closer the angle between the normal vector and the `k vector is to pi/2 (a right angle), the greater will be the area of the region on our glass pane.  As this angle approaches pi/2, the length of the rectangle on the glass pane approaches infinity, and so therefore does its area.

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Recall the definition of the dot product of two vectors as the product of their magnitudes and the cosine of the angle between them.  It follows immediately that the cosine of the angle between the vectors is equal to the dot product divided by the product of their magnitudes.

The angle gamma between the vectors `N and `k is therefore characterized by

cos(gamma) = `N dot `k / ( || `N || * || `k || ). 

For the given vector `N we have

cos(gamma) = (2 `i + 3 `j + 4 `k) dot `k / ( (sqrt(2^2 + 3^2 + 4^2) * 1 ) = 4 / sqrt(29).

It follows that the area of the pane above our unit square W is 1 / (4 / sqrt(29)) = sqrt(29) / 4, or roughly 1.35.

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  `q004.  Suppose some surface (perhaps a sphere, or a quadric surface of some kind) lies above an area increment `dx by `dy of the xy plane containing sample point (x_hat, y_hat).  As you are aware, if we know the equation of that surface we can use partial derivatives to calculate a vector normal to the surface at the point directly above (x_hat, y_hat).

If we find that the normal vector is 2 x_hat `i + y_hat `j + `k, then what is the expression for the area of that part of our surface lying directly above the `dx by `dy area increment of the xy plane?

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

The vector 2 x_hat `i + y_hat `j + `k makes angle gamma with the vertical `k vector, such that

cos(gamma) = (2 x_hat `i + y_hat `j + `k) dot `k / (|| 2 x_hat `i + y_hat `j + `k || || `k || )

= 1 / (sqrt( 4 x_hat^2 + y_hat^2 + 1) ).

The area on the surface of the `dx by `dy increment therefore exceeds the area of the increment in the xy plane by factor 1 / cos(gamma) = sqrt(4 x_hat^2 + y_hat^2 + 1), so the are of the surface above our xy increment is

`dS = sqrt(4 x_hat^2 + y_hat^2 + 1) * `dx * `dy.

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

`q005.  If the surface above the xy plane is given by the function z = f(x, y), then what is the expression for a normal vector above the point (x_hat, y_hat), and what is the cosine of the angle it makes with the `k vector?

Let's let `dS be the part of our surface that lies directly above our `dx by `dy increment of the xy plane.

What would be the area of `dS, in terms of `dx, `dy, the coordinates (x_hat, y_hat) of our sample point, and our function f(x,y) along with any necessary derivatives?.

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution:  As you know from the earlier work in this course, the vector (f_x `i + `k) X (f_y `i + `k) = - f_x `i - f_y `j + `k is normal to the surface at the point ( x, y, f(x,y) ).  So the angle gamma between this normal vector and the `k vector satisfies

cos(gamma) = ( - f_x `i - f_y `j + `k ) dot `k / ( || - f_x `i - f_y `j + `k || * || `k || ) = 1 / (f_x^2 + f_y^2 + 1).

We have assumed in the above that all functions are evaluated at (x, y) = (x_hat, y_hat).  So our expression for cos(gamma), if written out completely, would be

cos(gamma) = 1 / (f_x^2(x_hat, y_hat) + f_y^2(x_hat, y_hat) + 1).

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

`q006.  Let f(x, y) = 3 x^2 + 5 y^2 - 2 xy.

Let `dA by an area increment with dimensions `dx = .003 and `dy = .005, containing the point (1, 2).

What is your best approximation of the area of the region on the graph of z = f(x, y), lying above the given increment?

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

All we need to do is figure out the angle gamma between the vector normal to the surface and the vector `k; in fact all we need is the cosine of gamma.

This is easily found.  At the point (1, 2) the vectors f_x `i + `k and f_y `j + `k are both tangent to the surface, so their cross product -f_y `i - f_x `j + `k will be normal to the surface. 

At (1, 2) we have f_x = 6 x - 2 y = 6 * 1 - 2 * 2 = 2, and f_y = 10 y - 2 x = 10 * 2 - 2 * 1 = 18.  The cross product is thus

( f_x `i + `k ) X ( f_y `j + `k ) = -f_y `i - f_x `j + `k = -18 `i - 2 `j + `k.

By the definition of dot product, the cosine of the angle gamma made by this vector with the `k axis has cosine given by

cos(gamma) = ( -18 `i - 2 `j + `k ) dot `k / ( || -18 `i - 2 `j + `k || || `k || ) = 1 / sqrt( (-18)^2 + (-2)^2 + 1^2) ) = 1 / sqrt(329), or very approximately .055.

Note that cos(gamma) is pretty close to zero, indicating that the angle gamma between the normal vector and the `k vector is pretty close to 90 degrees.  This means that the surface area increment is pretty close to vertical, so that its area will be much greater than that of the increment `dA in the xy plane.

The area of the increment `dS on the surface, lying about the region `dA in the plane, is thus

`dS = `dA / cos(gamma) = `dA / .055 = 18 * `dA, approximately.

The area of the increment `dA , which is a square with dimensions .003 by .005, is .000015 so the area of `dS is .000015 * 18 = .00027.

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  Find the area `dS of the surface area increment of the surface given in the preceding, corresponding to a typical area increment `dA of the xy plane, containing sample point (x_hat, y_hat).

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

The reasoning is at every step similar to that used in the preceding.  The only difference is that we use (x_hat, y_hat) instead of (1, 2).

As before,

f_x = 6 x - 2 y and f_y = 10 y - 2 x,

so at the point (x_hat, y_hat) we have

f_x = 6 h_hat - 2 y_hat and f_y = 10 y_hat - 2 x_hat

so that our normal vector is

( f_x `i + `k ) X ( f_y `j + `k ) = -f_y `i - f_x `j + `k = -(10 y_hat - 2 x_hat) `i - (6 x_hat - 2 y_hat) `j + `k.

The cosine of the angle gamma is therefore given by

cos(gamma) = 1 / sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1)

and the area of the region `dS is

`dS = sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dA

= sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy.

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

`q008.  What Riemann sum corresponds to the area of the surface in the preceding two problems, lying above the disk bounded by the circle x^2 + y^2 = 2?

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

The region x^2 + y^2 <= 2 can be easily partitioned in either of two ways. 

If we consider cross-sections parallel to the y axis, there is a cross-section for every value of x between x = -2 and x = 2. 

Solving the equation x^2 + y^2 = 2 for y, we get y = +- sqrt( 2 - x^2).  It follows that for a given x, the region extends from y = - sqrt(2 - x^2) to y = sqrt(2 - x^2).

Thus our description of the region is

-2 <= x <= 2

-sqrt(2 - x^2) <= y <= sqrt(2 - x^2).

For a given subinterval of -2 <= x <= 2, the subinterval having length `dx and sample point x_hat, the corresponding subregion consists of a 'strip' of width `dx, running over the y interval

-sqrt(2 - x^2) <= y <= sqrt(2 - x^2)

If we the partition the y interval

-sqrt(2 - x^2) <= y <= sqrt(2 - x^2)

into subintervals of length `dy, each containing a sample point the 'strip' becomes a series of area increments, each with dimensions `dx by `dy. 

The typical area interval `dA will therefore have area `dx * `dy and will contain sample point (x_hat, y_hat).  The area of the surface directly above this area increment will be

`dS = sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy,

as seen in the preceding problem.

The area of the surface above our 'strip' will therefore be the sum of all the incremental surface areas sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy, where the y_hat values are bounded below by -sqrt(2 - x^2) and above by sqrt(2 - x^2).  We can write this sum as

area above 'strip' = sum (sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy, -sqrt(2 - x^2) <= y_hat <= sqrt(2 - x^2)).

There is such a 'strip' for each of our subintervals of the x axis.  To get the area of the entire surface lying about x^2 + y^2 = 2 we must sum the areas of these strips.  Since x values can run from -2 to 2, we can say the following:

total area = sum ( 'strip' areas, -2 <= x_hat <= 2)

= sum ( sum (sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy, -sqrt(2 - x^2) <= y_hat <= sqrt(2 - x^2), - sqrt(2 - x^2) <= x_hat <= sqrt(2 - x^2)).

We could get a little more formal about this, using subscripts i and j to refer to the specific area increments, but this should convey the idea.

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

`q009. 

What integral comes from taking the limit of the Riemann sums?

(Note: Don't attempt to perform the integration, which probably cannot be done except by approximation).

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

The Riemann sum

sum ( sum (sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy, -sqrt(2 - x^2) <= y_hat <= sqrt(2 - x^2), - sqrt(2 - x^2) <= x_hat <= sqrt(2 - x^2))

approaches the integral as `dx and `dy approach zero.  When this occurs the difference between the x and y values in a given increment, and the sample-point values x_hat and y_hat, becomes insignificant, and the sums become integrals.  So the expression

sqrt((10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) )

becomes, in the limit,

sqrt((10 y - 2 x)^2 + (6 x - 2 y)^2).

`dx and `dy become dx and dy.

The limits on our x values, and the limits of they values in our 'strip' become limits on the integral.  We end up with the integral

integral ( integral ( sqrt((10 y - 2 x)^2 + (6 x - 2 y)^2) ) dy, y from -sqrt(2-x^2) to (sqrt(2-x^2) )  dx, x from -2 to 2)

In standard notation this looks like

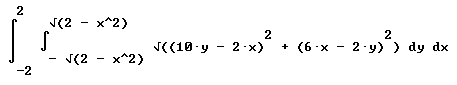
Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

`q010.  Suppose the surface in the above has, at the point lying above (x, y), an area density equal to 6 - x - y. 

How would the analysis in the preceding series of problems need to be modified in order to find the mass of the surface above the region x^2 + y^2 <= 2?

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Recall that the typical surface area increment was

`dS = sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy.

To get the approximate mass of the region the density would be evaluated at the sample point (x_hat, y_hat) and multiplied by the area.  At the sample point, the density would be ( 6 - x_hat - y_hat ), so the mass increment would be

`dm = density * area = ( 6 - x_hat - y_hat ) * `dS = ( 6 - x_hat - y_hat ) * sqrt( (10 y_hat - 2 x_hat)^2 + (6 x_hat - 2 y_hat)^2 + 1) * `dx * `dy.

The Riemann sum would be similarly modified, with the same limits on x and y, so that the sum would approach the integral

integral ( integral ( (6 - x - y) sqrt((10 y - 2 x)^2 + (6 x - 2 y)^2) ) dy, y from -sqrt(2-x^2) to (sqrt(2-x^2) )  dx, x from -2 to 2).

In standard notation this would look like the following:

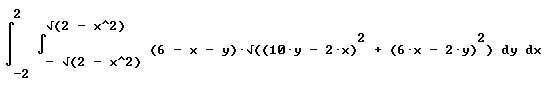
Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  `q011. 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  `q012. 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question: 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating:

Question:  &&&

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique rating: