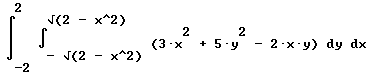
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.
Question: `q001. In the preceding qa, we considered the function
z = f(x, y) = 3 x^2 + 5 y^2 - 2 xy
and the portion of the surface z = f(x, y) lying above the region x^2 + y^2 = 2 of the xy plane.
We partitioned the region of the xy plane into subregions and found the surface area above each of these subregions, then summed them and took a limit in order to obtain an integral for the area of the surface above the region of the xy plane.
For the typical subregion of the xy plane having dimensions `dx by `dy and containing sample point (x_hat, y_hat), how far above the point (x_hat, y_hat, 0) is the point of the surface z = f(x, y)?
What therefore is our approximation of the volume of the region lying above our increment of the xy plane, and the surface?
Your solution:
Confidence rating:
Given Solution: The distance from the (x, y) plane to the surface is just the value of z = f(x, y) at the given point. The sample point has x and y coordinates x_hat and y_hat, so the height of the surface is
height = f(x_hat, y_hat) = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat.
The region lying above our `dx by `dy rectangle in the xy plane, and below the graph of z = f(x, y), therefore has a rectangular base whose area is `dx by `dy, and approximate altitude 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat.
It should be clear that the volume of this region is `dx * `dy * altitude = ( 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) `dx `dy.
Self-critique (if necessary):
Self-critique rating:
Question: What therefore would be the total volume of the region lying above the region x^2 + y^2 <= 2 of the xy plane, and the surface z = f(x, y)?
Your solution:
Confidence rating:
Given Solution: The volume of the typical region is
`dV = `dx * `dy * altitude = ( 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) `dx `dy.
This expression could be put into a Riemann sum, which sums up the volumes corresponding to all the area increments. The Riemann sum could then be allowed to approach an integral. You should do so, but the steps will not be repeated here. They are completely analogous, except for the use of the altitude expression ( 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) , to the expressions developed previously for surface area.
The resulting integral is
integral ( integral ( `dx * `dy * altitude = ( 3 x^2 + 5 y^2 - 2 x y ) dy, y from -sqrt(2 - x^2) to x(2 - x^2)) dx, x from -2 to 2).
In standard notation the integral looks like this:
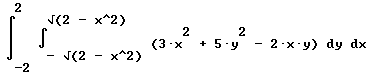
Self-critique (if necessary):
Self-critique rating:
Question: `q003. How could we describe, in terms of inequalities in x, y and z, the 3-dimensional region whose volume integral we found in the preceding?
Your solution:
Confidence rating:
Given Solution:
For any point (x, y) in the xy plane, the surface z = f(x, y) = ( 3 x^2 + 5 y^2 - 2 x y ) lies at height ( 3 x^2 + 5 y^2 - 2 x y ) above the xy plane.
The region x^2 + y^2 <= 2 can be described by
-x <= 2 <= 2
-sqrt(2-x^2) <= y <= sqrt(2 - x^2)
and for any such point (x, y), the z coordinate will be between 0 and ( 3 x^2 + 5 y^2 - 2 x y ). Thus the complete description of the region is
-2 <= x <= 2
-sqrt(2-x^2) <= y <= sqrt(2 - x^2)
0 <= z <= ( 3 x^2 + 5 y^2 - 2 x y )
Self-critique (if necessary):
Self-critique rating:
Question: `q004. key idea: if you have an expression for the typical interval, and a description of the region, you can form the Riemann sum and use it to both derive and understand the integral
The 3-dimensional region between the xy plane and the surface z = 3x^2 + 5y^2 - 2xy is described by
-2 <= x <= 2
-sqrt(2 - x^2) <= y <= sqrt(2 - x^2)
0 <= z <= ( 3 x^2 + 5 y^2 - 2 x y ).
A typical volume increment within this region can be said to have dimensions `dx by `dy by `dz, and sample point (x_hat, y_hat, z_hat).
If wewe will have a region of the xy plane having dimensions `dx by `dy and containing sample point (x_hat, y_hat).
If we now partition the interval lying between the xy plane and our surface into subintervals each having length `dz, what will be the maximum and minimum z values encountered?
Our sample point is (x_hat, y_hat). The value of our function z = 3 x^2 + 5 y^2 - 2 xy at this point is 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat. The z interval will start at the xy plane, where z = 0, and end at the surface, where z = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat. The z interval will therefore be
0 <= z <= 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat.
The region above our chosen `dx by `dy area increment in the xy plane, which contains sample point (x_hat, y_hat), will run from z = 0 to about z = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat (above the sample point that is exactly how far the region will run; there will almost certainly be some points in our area increment above which the surface is encountered for slightly lesser z values, and some where the z values will be greater; however if our increments are small, these differences will be small).
A typical interval of our z partition will have length `dz and will contain sample point z_hat. Within this z interval, and above our selected `dx by `dy increment, we will have a rectangular 'box' with dimensions `dx by `dy by `dz. What is the sample point within this box, and what is the volume of the box?
The z coordinate of the sample point will be z_hat. The x and y coordinates will be x_hat and y_hat. The 'box' will be our volume increment. So the sample point within the 'box' is (x_hat, y_hat, z_hat).
The volume of the 'box' is `dx * `dy * `dz.
Let's think of the region above the `dx by `dy area increment as a 'stack' of such boxes. All contain sample points with x and y coordinates x_hat and y_hat. Each box in the stack is represented by a different z coordinate, i.e., a different z_hat.
The area increment that forms the base of this 'stack' is one of the area increments in the 'strip' running from y = -sqrt(2 - x_hat^2) to y = sqrt(2 - x_hat^2). This 'strip' is partitioned into increments of length `dy. Each of these increments forms a 'stack' running from the xy plane to the surface z = 3 x^2 + 5 y^2 - 2 x y. All these stacks together form a thin slice of the region between the xy plane and our surface. If we add the volumes of all the `dx by `dy by `dz increments in all the stacks supported by the strip, we get the volume of this thin slice.
Now our thin slice has thickness `dx and is represented by sample point x = x_hat. There are other similar slices, one for each of the subintervals in our partition of the x interval -2 <= x <= 2. Each of these slices has thickness `dx, and a volume equal to the sum of the volumes of all the 'stacks' within the y 'strip', with each stack running from the xy plane to our surface. If we add the volumes of all these slices, we get an approximation to the volume between the xy plane and our surface. If we let our `dx and `dy and `dz increments all approach zero, the error that arises by using the single value 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat to represent the height of the 'stack' approaches zero, and the total of the volumes of all our 'boxes' will approach the area we are seeking.
Write the Riemann sum for the volume of the 'stack' above an area increment of the xy plane having dimensions `dx by `dy and containing sample point (x_hat, y_hat, 0).
What integral would this Riemann sum approach if we allowed `dz to approach zero?
What does this integral represent?
The 'stack' runs from z = 0 to z = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat . Each volume increment has volume `dV = `dx * `dy * `dz. So we might write the Riemann sum as
sum ( `dx * `dy * `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ).
As `dz approaches zero, `dx and `dy are unaffected, as are x_hat and y_hat. The differences between z coordinates within a `dz subinterval become insignificant so z_hat becomes replaced by z, and `dz becomes dz. Our integral will be
integral ( (`dx * `dy) dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat).
This integral represents the exact volume of a 'stack' with base area `dx by `dy and height 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat. (This is something we could have easily enough calculated without resorting to integration. But we will shortly revisit this region with a density function that does require integration, and it's very useful to understand the process of setting up the integral in the simplest possible application, that of finding the volume).
Since the integrand `dx * `dy has no z dependence, the `dx * `dy (representing the area at the base of the 'stack', which is common to all 'boxes' in the 'stack', `dx * `dy can be factored out of the Riemann sum or the integral to give us
approximate 'stack' volume = sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dx * `dy
exact volume of 'stack' based on sample point = integral ( dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat) * `dx * `dy
Now form the Riemann sum for the volume of the 'slice' corresponding to the `dx interval containing sample point x = x_hat.
That 'slice' consists of many 'stacks', one for each subinterval of the partition of the y-interval
-sqrt(2 - x_hat^2) <= y <= sqrt(2 - x_hat^2).
Each subinterval has length `dy and contains sample point y_hat; each 'stack' has volume
sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dx * `dy
which in the limit as `dz approaches zero yields
integral ( dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat) * `dx * `dy
approximating the actual volume lying above the `dx by `dy area increment at its base.
The volume of the 'slice' is obtained by simply adding up the volumes of the 'stacks' lined up along the line x = x_hat from y = -sqrt(2-x_hat^2) to y = sqrt(2 - x_hat)^2, so that
'slice' volume is approximately
sum( sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dx * `dy ), y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ). Since `dx is the same for all 'stacks' in the 'slice' it can be factored out to yield
sum( sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dy, y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx
As seen previously the inner sum approaches an integral, so our expression can be written
sum( integral ( dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat) ) * `dy, y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx
If we allow `dy to approach zero, the y_hat value in the `dx by `dy each area increment becomes indistinguishable from the other y values in the increment, so that y_hat becomes y, `dy becomes dy, resulting in the limiting value
integral ( integral ( dz, z from 0 to 3 x_hat^2 + 5 y^2 - 2 x_hat y) ) dy, y running from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx
Finally form the Riemann sum for the volume of all the 'slices' corresponding to `dx intervals each containing its own x = x_hat sample point.
All that remains is to add up the volumes of the 'slices'. Since x values run from x = -2 to x = 2, the Riemann sum is
sum(sum( sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dy, y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx , x running from -2 to 2).
This Riemann sum approaches the integral
integral( integral ( integral ( dz, z from 0 to 3 x^2 + 5 y^2 - 2 x y) dy, y from -sqrt(2-x^2) to sqrt(2 - x^2) ) dx , x from -2 to 2).
In standard form this integral is written
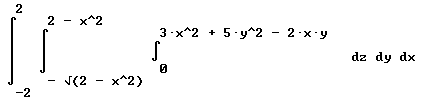
Now repeat the entire process to find the mass of this region, given the mass density function
density(x, y, z) = x + y^2 + sqrt(z) + 1.
The typical volume increment is a `dx by `dy by `dz increment with sample point (x_hat, y_hat, z_hat). The volume of the increment is `dx * `dy * `dz, and the density x + y^2 + sqrt(z) + 1, evaluated at the sample point, is x_hat + y_hat^2 + sqrt( z_hat ) + 1.
The mass of the volume increment thus approximated by
`dm = density * volume = (x_hat + y_hat^2 + sqrt( z_hat ) + 1) * `dx * `dy * `dz.
The region is the same as before, so all the limits on the sums and integrals are identical to those in the preceding.
For example the mass of the typical 'stack' is
sum ( (x_hat + y_hat^2 + sqrt( z_hat ) + 1) * `dx * `dy * `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ).
The expressions for the approximate mass of the typical 'slice', for the approximate mass of the entire region, and for the exact mass of the entire region are developed similarly in a manner nearly identical to that used to find the volume. The integral we obtain at the end is
integral( integral ( integral ( (x_hat + y_hat^2 + sqrt( z_hat ) + 1) dz, z from 0 to 3 x^2 + 5 y^2 - 2 x y) dy, y from -sqrt(2-x^2) to sqrt(2 - x^2) ) dx , x from -2 to 2),
expressed in standard notation as
Find the integral for the volume of the region where the cylinder x^2 + y^2 = 4 intersects the ellipsoid x^2 / 4 + y^2 / 9 + z^2 / 16 = 1, and for the mass of that region if density = 1 / sqrt(x^2 + y^2 + 1). Do the integration where possible.
What complication arises in the preceding question if the equation of the cylinder is changed to x^2 + y^2 = 9?
havent lost int; have just given up on any sustained recip
liter divided into cm^3 ...
Your solution:
Confidence rating:
Given Solution:
Our sample point is (x_hat, y_hat). The value of our function z = 3 x^2 + 5 y^2 - 2 xy at this point is 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat. The z interval will start at the xy plane, where z = 0, and end at the surface, where z = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat. The z interval will therefore be
0 <= z <= 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat.
Self-critique (if necessary):
Self-critique rating:
Question:
`q005.
The region above our chosen `dx by `dy area increment in the xy plane, which contains sample point (x_hat, y_hat), will run from z = 0 to about z = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat (above the sample point that is exactly how far the region will run; there will almost certainly be some points in our area increment above which the surface is encountered for slightly lesser z values, and some where the z values will be greater; however if our increments are small, these differences will be small).
A typical interval of our z partition will have length `dz and will contain sample point z_hat. Within this z interval, and above our selected `dx by `dy increment, we will have a rectangular 'box' with dimensions `dx by `dy by `dz. What is the sample point within this box, and what is the volume of the box?
Your solution:
Confidence rating:
Given Solution: The z coordinate of the sample point will be z_hat. The x and y coordinates will be x_hat and y_hat. The 'box' will be our volume increment. So the sample point within the 'box' is (x_hat, y_hat, z_hat).
The volume of the 'box' is `dx * `dy * `dz.
Self-critique (if necessary):
Self-critique rating:
Question:
`q006. Let's think of the region above the `dx by `dy area increment as a 'stack' of such boxes. All contain sample points with x and y coordinates x_hat and y_hat. Each box in the stack is represented by a different z coordinate, i.e., a different z_hat.
The area increment that forms the base of this 'stack' is one of the area increments in the 'strip' running from y = -sqrt(2 - x_hat^2) to y = sqrt(2 - x_hat^2). This 'strip' is partitioned into increments of length `dy. Each of these increments forms a 'stack' running from the xy plane to the surface z = 3 x^2 + 5 y^2 - 2 x y. All these stacks together form a thin slice of the region between the xy plane and our surface. If we add the volumes of all the `dx by `dy by `dz increments in all the stacks supported by the strip, we get the volume of this thin slice.
Now our thin slice has thickness `dx and is represented by sample point x = x_hat. There are other similar slices, one for each of the subintervals in our partition of the x interval -2 <= x <= 2. Each of these slices has thickness `dx, and a volume equal to the sum of the volumes of all the 'stacks' within the y 'strip', with each stack running from the xy plane to our surface. If we add the volumes of all these slices, we get an approximation to the volume between the xy plane and our surface. If we let our `dx and `dy and `dz increments all approach zero, the error that arises by using the single value 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat to represent the height of the 'stack' approaches zero, and the total of the volumes of all our 'boxes' will approach the area we are seeking.
Write the Riemann sum for the volume of the 'stack' above an area increment of the xy plane having dimensions `dx by `dy and containing sample point (x_hat, y_hat, 0).
What integral would this Riemann sum approach if we allowed `dz to approach zero?
What does this integral represent?
Your solution:
Confidence rating:
Given Solution:
The 'stack' runs from z = 0 to z = 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat . Each volume increment has volume `dV = `dx * `dy * `dz. So we might write the Riemann sum as
sum ( `dx * `dy * `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ).
As `dz approaches zero, `dx and `dy are unaffected, as are x_hat and y_hat. The differences between z coordinates within a `dz subinterval become insignificant so z_hat becomes replaced by z, and `dz becomes dz. Our integral will be
integral ( (`dx * `dy) dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat).
This integral represents the exact volume of a 'stack' with base area `dx by `dy and height 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat. (This is something we could have easily enough calculated without resorting to integration. But we will shortly revisit this region with a density function that does require integration, and it's very useful to understand the process of setting up the integral in the simplest possible application, that of finding the volume).
Since the integrand `dx * `dy has no z dependence, the `dx * `dy (representing the area at the base of the 'stack', which is common to all 'boxes' in the 'stack', `dx * `dy can be factored out of the Riemann sum or the integral to give us
approximate 'stack' volume = sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dx * `dy
exact volume of 'stack' based on sample point = integral ( dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat) * `dx * `dy
Self-critique (if necessary):
Self-critique rating:
Question: `q007.
Now form the Riemann sum for the volume of the 'slice' corresponding to the `dx interval containing sample point x = x_hat.
Your solution:
Confidence rating:
Given Solution:
That 'slice' consists of many 'stacks', one for each subinterval of the partition of the y-interval
-sqrt(2 - x_hat^2) <= y <= sqrt(2 - x_hat^2).
Each subinterval has length `dy and contains sample point y_hat; each 'stack' has volume
sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dx * `dy
which in the limit as `dz approaches zero yields
integral ( dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat) * `dx * `dy
approximating the actual volume lying above the `dx by `dy area increment at its base.
The volume of the 'slice' is obtained by simply adding up the volumes of the 'stacks' lined up along the line x = x_hat from y = -sqrt(2-x_hat^2) to y = sqrt(2 - x_hat)^2, so that
'slice' volume is approximately
sum( sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dx * `dy ), y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ). Since `dx is the same for all 'stacks' in the 'slice' it can be factored out to yield
sum( sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dy, y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx
As seen previously the inner sum approaches an integral, so our expression can be written
sum( integral ( dz, z from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat) ) * `dy, y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx
If we allow `dy to approach zero, the y_hat value in the `dx by `dy each area increment becomes indistinguishable from the other y values in the increment, so that y_hat becomes y, `dy becomes dy, resulting in the limiting value
integral ( integral ( dz, z from 0 to 3 x_hat^2 + 5 y^2 - 2 x_hat y) ) dy, y running from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx
Self-critique (if necessary):
Self-critique rating:
Question: `q008. Finally form the Riemann sum for the volume of all the 'slices' corresponding to `dx intervals each containing its own x = x_hat sample point.
All that remains is to add up the volumes of the 'slices'. Since x values run from x = -2 to x = 2, the Riemann sum is
sum(sum( sum ( `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ) * `dy, y running by increment `dy from -sqrt(2-x_hat^2) to sqrt(2 - x_hat^2) ) * `dx , x running from -2 to 2).
This Riemann sum approaches the integral
integral( integral ( integral ( dz, z from 0 to 3 x^2 + 5 y^2 - 2 x y) dy, y from -sqrt(2-x^2) to sqrt(2 - x^2) ) dx , x from -2 to 2).
In standard form this integral is written
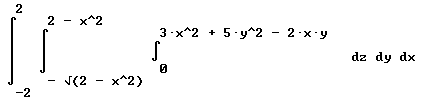
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
`q009. Now repeat the entire process to find the mass of this region, given the mass density function
density(x, y, z) = x + y^2 + sqrt(z) + 1.
Your solution:
Confidence rating:
Given Solution:
The typical volume increment is a `dx by `dy by `dz increment with sample point (x_hat, y_hat, z_hat). The volume of the increment is `dx * `dy * `dz, and the density x + y^2 + sqrt(z) + 1, evaluated at the sample point, is x_hat + y_hat^2 + sqrt( z_hat ) + 1.
The mass of the volume increment thus approximated by
`dm = density * volume = (x_hat + y_hat^2 + sqrt( z_hat ) + 1) * `dx * `dy * `dz.
The region is the same as before, so all the limits on the sums and integrals are identical to those in the preceding.
For example the mass of the typical 'stack' is
sum ( (x_hat + y_hat^2 + sqrt( z_hat ) + 1) * `dx * `dy * `dz, z running by increment `dz from 0 to 3 x_hat^2 + 5 y_hat^2 - 2 x_hat y_hat ).
The expressions for the approximate mass of the typical 'slice', for the approximate mass of the entire region, and for the exact mass of the entire region are developed similarly in a manner nearly identical to that used to find the volume. The integral we obtain at the end is
integral( integral ( integral ( (x_hat + y_hat^2 + sqrt( z_hat ) + 1) dz, z from 0 to 3 x^2 + 5 y^2 - 2 x y) dy, y from -sqrt(2-x^2) to sqrt(2 - x^2) ) dx , x from -2 to 2),
expressed in standard notation as
Self-critique (if necessary):
Self-critique rating:
Question:
`q010. Find the integral for the volume of the region where the cylinder x^2 + y^2 = 4 intersects the ellipsoid x^2 / 4 + y^2 / 9 + z^2 / 16 = 1, and for the mass of that region if density = 1 / sqrt(x^2 + y^2 + 1). Do the integration where possible.
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question: `q011. What complication arises in the preceding question if the equation of the cylinder is changed to x^2 + y^2 = 9?
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question: `q012.
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question:
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question: &&&
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating: