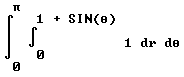
If your solution to stated problem does not match the given solution, you should self-critique per instructions at

   http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm

.

Your solution, attempt at solution.  If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it.  This response should be given, based on the work you did in completing the assignment, before you look at the given solution.

At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises. 

Question:  `q001.  Evaluate the double integral Int( Int(dr, 0, 1 + sin(theta)) dθ), 0 , pi). Sketch and describe the region of integration.

In standard notation the integral is

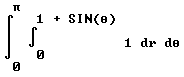
Your solution: 

Confidence rating:
 

Given Solution: 

An antiderivative of 1 is r.  The change in the antiderivative between r = 0 and r = 1 + sin(theta) is 1 + sin(theta).

Integrating this result with respect to theta we get antiderivative theta - cos(theta). 

The change in this quantity between theta = 0 and theta = pi is

pi - cos(pi) - (0 - cos(0) ) = pi - (-1) - (-1) = pi + 2.

Additional note:

Between theta = 0 and theta = pi the value of sin(theta) goes from 0 to 1 and back to 0, so the value of 1 + sin(theta) goes from 1 to 2 to 1. 

The graph of 1 + sin(theta) from theta value 0 to 2 pi is given below, and the portion of the graph from theta values 0 to pi is in light blue, the portion above the x axis.  It should be clear that this region contains a circle of radius 1 (visualize the circle centered at (0, 1)) and therefore has somewhat more area.  The area of the circle would be pi, so the result pi + 2 makes good sense.

Self-critique (if necessary):

Self-critique rating:

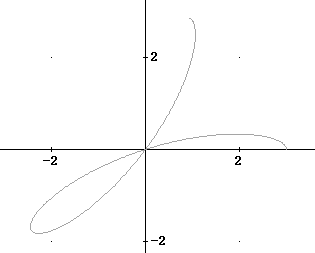
Question:  `q002.  Use a double integral to find the area of the region described by 0 <= r <= 3 cos(5theta)

You should know from precalculus how to construct this graph, and how to test for various symmetries.

Between theta = 0 and theta = 2 pi, cos(5 theta) goes through 5 complete cycles from 1 to 0 to -1 and back to 0.  Each cycles takes place in an angular distance of 2 pi / 5 (in degrees this is 72 degrees). 

The figure below depicts the graph from theta = 0 to theta = 2 pi / 5.

The graph below adds the portion corresponding to theta = 2 pi / 5 to theta = 4 pi / 5, which appears in red.

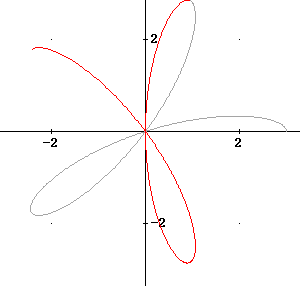
The graph for theta = 4 pi / 5 to theta = 6 pi / 5 appears in green.  Note that this graph traces over half the graph from theta = 0 to theta = 2 pi / 5.

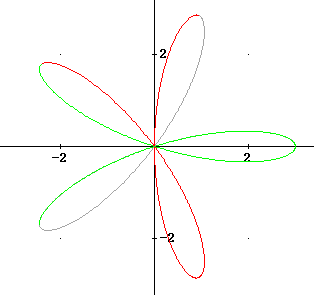
The graph for theta = 6 pi / 5 to theta = 8 pi / 5 traces over more of the previous graphs, and adds nothing to the existing curve.

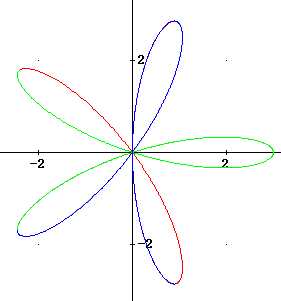
The graph for theta = 0 to theta = pi, in fact, completes the entire graph:

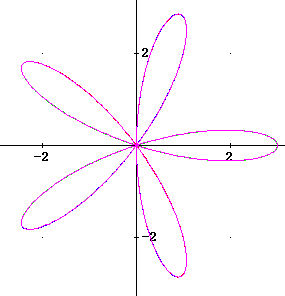
So the graph of r = 3 cos(5 theta) forms a sort of 5-leaved clover, and the domain 0 <= theta <= pi is sufficent to trace the region once.

A single 'leaf' is formed between theta = - pi/5 and theta = pi / 5.  The area of the entire graph is therefore 5 times the area of this 'leaf'.

If this 'leaf' is partitioned into area increments, with typical area increment defined by the incremental angle `dTheta and increment `dr and containing sample point (r_hat, theta_hat), then the area of the increment is r `dTheta * `dr.  The area does not depend on the sample point; if we were for example integrating to find mass then the mass density at the sample point would be important, and if we wished to find moment of inertia the density at the sample point and the r coordinate r_hat would be important.

The area of the 'leaf' is the total of the areas of the increments, and the resulting Riemann sum leads to the integral int( int( (1 * r dr), 0, 3 cos(theta)) dTheta, -pi/5, pi/5)   In standard notation the integral is

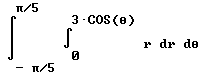
The integral is easily evaluated.  Using r^2 / 2 as our antiderivative of r, we find that the change in antiderivative for the inner integral is 9 cos^2(theta).

Integrating 9 cos^2(theta) we find that an antiderivative is 9 ( sin(theta) cos(theta) / 2 + theta / 2 ).  It is possible using trigonometric formulas to get an exact expression for the values of this expression at theta = pi/5 and theta = - pi/5, but the approximation 4.967 is about as well as we can normally expect to do. 

We can, however, get an exact solution.  The antiderivative we obtained could easily be evaluated at theta = 0 and at theta = pi.  This suggests just integrating over the entire domain.

The integral would be the same as before, except that limits on the theta integral would be 0 and pi rather than -pi/5 and pi/5.  Our antiderivative would still be 9 ( sin(theta) cos(theta) / 2 + theta / 2 ).  The change in the antiderivative from theta = 0 to theta = pi would be

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  `q003.  Use polar coordinates to find the double integral of f(x,y) = ln( a^2 + x^2 + y^2) over D with respect to A where D is the circular disk defined by x^2 + y^2 <= a^2 for some a > 0.

Your solution: 

Confidence rating:
 

Given Solution: 

Using the conversions x = r cos(theta) and y = r sin(theta) we find that the disk x^2 + y^2 = a^2 is just r^2 cos^2(theta) + r^2 sin^2(theta) = a^2, or r = a (recall that sin^2(theta) + cos^2(theta) = 1).

Our function f(x, y) becomes f(r, theta) = ln(a^2 + r^2).

Our circular region is just 0 <= r <= a, 0 <= theta <= 2 pi.

Our integral is therefore int(int ( ln(a^2 + r^2) dr, 0, a), dTheta, 0, 2 pi).

The integral, and the inner integral, are shown below in standard form.

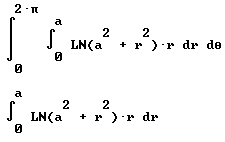
Our 'inner integral' is evaluated by the substitution u = a^2 + r^2, so that du = 2 r dr and our existing r dr is 1/2 du. 

INT( ln(u) du / 2) = 1/2 (u ln(u) - u) + c, where c is an integration constant.   Using 1/2 (u ln(u) - u) = 1/2 ( (a^2 + r^2) ln((a^2 + r^2) ) - (a^2 + r^2) ) as our antiderivative we find that from r = 0 to r = a, the antiderivative changes by a^2 ln(2 a) - a^2 / 2.

Our outer integral will therefore be

int(  (a^2 ln(2 a) - a^2 / 2) dTheta, theta, 0, 2 pi) = (a^2 ln(2 a) - a^2 / 2) * 2 pi = 2 pi a^2 ln(2 a) - pi a^2.

Self-critique (if necessary):

Self-critique rating:

Question:  `q004.  Find the volume of the solid bounded above by the sphere x^2 + y^2 + z^2 = 2 and below by the parabola z = x^2 + y^2.

Your solution: 

Confidence rating:
 

Given Solution: 

We must first find the curve of intersection between these two surfaces.

We could substitute z = x^2 + y^2 for z in the first equation, obtaining the equation (x^2 + y^2) ^ 2 + x^2 + y^2 = 2.

Expanding the square and substituting u = x^2 and v = y^2 we would get the equation u^2 + 2 u v + v^2 + u + v = 52 

We could try to complete the square but that u v term looks hopeless.  It isn't really so, but there has to be an easier way to proceed.

We resort to a common shortcut.  We note that x^2 + y^2 occurs in both equations.  Furthermore, in polar coordinates x^2 + y^2 = r^2, so our equations can be written

r^2 + z^2 = 2 and

z = r^2.

This looks better than what we had before, so we proceed to eliminate z between the two equations.

Substituting r^2 for z in the first equation gives us

r^2 + r^4 = 2.

Letting u = r^2 our equation becomes

u^2 + u - 2 = 0,

with solutions

u = 1, u = -2.

Since u = r^2, we have r = sqrt(1) = 1.  (Note that u = -2 doesn't yield a solution since sqrt(-2) is not defined.)

Thus the curve of intersection lies above the circle r = 1 in the x y plane.

Since the origin is on the graph of the parabola, but lies below the graph of the sphere, it follows that the sphere lies above the parabola for all points within this circle.

On a typical area increment `dA defined by `dTheta and `dr, with sample point (r_hat, theta_hat):

• The region between the parabola and the sphere consists of a cylinder whose cross-sectional area is `dA, and whose sample-point altitude extends from the parabola to the sphere above the point (r_hat, theta_hat). 

• The parabola lies at height z = r_hat^2 above the sample point, and the sphere at height sqrt( 2 - r^2 ). 

• The cross-sectional area `dA is roughly a rectangle of dimensions r_hat * `dTheta by `dr, and the altitude is sqrt(2 - r_hat^2) - r_hat^2, so the volume of the increment is (sqrt(2 - r_hat^2) - r_hat^2) * r_hat * `dr * `dTheta. 

• Summing over partitions of the intervals 0 <= r <= 1 and 0 <= theta <= 2 pi we obtain a Riemann sum, which approaches the integral

int (int( (sqrt(2 - r^2) - r^2) * r dr, 0, 1) dTheta, 0, 2 pi)

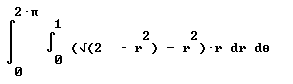
The inner integral is

int( (sqrt(2 - r^2) - r^2) * r dr, 0, 1) = int( sqrt(2 - r^2) * r dr, 0, 1) - int( r^3 dr, 0, 1) ,

which is fairly straightfoward (just let u = 2 - r^2 in the first, so that r dr = - 1/2 du, leaving int( -sqrt(u) / 2 du); and the integral of r^3 is very straightforward).

The result:

. 

The definite integral simplifies to very approximately .8

There is no theta dependence, so the integral with respect to theta just multiplies this result by 2 pi, leading to a final result of approximately 5.

Self-critique (if necessary):

Self-critique rating: