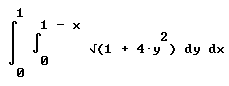
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.
... the magnitude of the projection of v onto w is cos(theta) times as great as the magnitude of v; the magnitude of v is therefore 1 / cos(theta) times as great as the magnitude of this projection ...
Question: `q001. Find the surface area of the portion of the surface z = y^2 that lies over the triangular region in the plane with vertices (0,0,0), (1,0,0) and (0,1,0).
Your solution:
Confidence rating:
Given Solution:
The triangular region is in the x y plane and is bounded by x axis, the y axis and the line y = 1 - x.
It can therefore be described by 0 <= x <= 1, 0 <= y <= 1 - x.
Quick solution:
We integrate sqrt(1 + f_x^2 + f_y^2) over the region.
For f(x, y) = 2 y, we have
sqrt(1 + f_x^2 + f_y^2) = sqrt( 1 + 4 y^2)
so our integral is
INT(INT(sqrt(1 + 4 y^2) dy, 1, 1 - x), dx, 0, 1),
which is approximately .63.
This makes sense, because the area of the triangular region is .5, and the parabolic region makes a relatively modest angle with vertical above most of the triangle.
Above the point (x, y), a vector normal to the surface z = y^2 is the cross product of i + f_x k and j + f_y k, where f(x, y) = y^2. This gives us the normal vector i X (j + 2 y k) = k - 2 y i.
Alternatively the surface z = f(x, y) is a level surface of the function F(x,y,z) = z - f(x, y). Since the gradient of this function is normal to the level surface, the vector del F(x, y, z) is normal to the surface.
In this case the surface is a level curve of F(x, y, z) = z - f(x, y) = z - y^2, so F_x = 0, F_y = -2 y and F_z = 1. The gradient is therefore 0 i - 2 y j + k., the same as that found previously.
In general the gradient of z - f(x, y) is -f_x i - f_y j + k, and the cosine of its angle with the k vector is 1 / sqrt( 1 + f_x^2 + f_y^2 ).
The unit normal to the xy plane is k, so the cosine of the angle between the normal to the surface and the normal to the xy plane is
cos(theta) = ( k - 2 y i ) dot k / | k - 2 y i | = 1 / sqrt( 1 + (2y)^2 ) = 1 / sqrt( 1 + 4 y^2 ).
The portion of the our surface which lies above an area increment `dA with dimensions `dx by `dy, located at (x_hat, y_hat) has an area that is equal to `dA, if the surface is parallel to the x y plane, and an area greater than `dA, if the surface is not parallel to the x y plane. The ratio of the areas is 1 / cos(theta) = sec(theta), where theta is the angle between the normal to the surface and the normal to the plane. The cosine of that angle was found above to be 1 / sqrt( 1 + 4 y^2 ). The reciprocal is sec(theta) = sqrt( 1 + 4 y^2 ). For the sample point (x_hat, y_hat) we have sec(theta) = sqrt( 1 + 4 y_hat^2 ).
So the surface area corresponding to our area increment is sqrt( 1 + 4 y_hat^2 ) `dA = sqrt( 1 + 4 y_hat^2 ) `dy `dx.
Our Riemann sum leads us to the integral
int ( int ( sqrt(1 + 4 y^2) dy, 0, 1 - x) dx, 0, 1)
STUDENT QUESTION
OK, except I got (5/6)=0.83 and you got 0.63??!?
INSTRUCTOR RESPONSE
.63 is correct to 2 significant figures.
5/6 can't be right. The integral is way too complicated for a rational-number
solution. Square roots, at the very least, would be required.
An antiderivative for the y integral is
ln(sqrt(4y^2 + 1) + 2y)/4 + y* sqrt(4 y^2 + 1)/2.
You get this by starting with the trig substitution y = tan(theta) / 4. You use
the identity 1 + tan^2(theta) = sec^2(theta), and y ' = tan(theta) sec(theta) /
4 so dy = 1/4 tan(theta) sec(theta) dTheta. Fairly straightforward, if you're up
on trig substitution.
Self-critique (if necessary):
Self-critique rating:
Question: `q002. Find the surface area of the portion of the sphere x^2 + y^2 + z^2 = 36 that lies above the plane z = 4.
The result is 24 pi.
Your solution:
Confidence rating:
Given Solution:
The sphere intersects the plane when
x^2 + y^2 + 4^2 = 36 so that
x^2 + y^2 = 20.
This describes a circle of radius 2 sqrt(5) centered at the origin.
This circle can be described by
-2 sqrt(5) <= x <= 2 sqrt(5)
-sqrt(20 - x^2) <= y <= sqrt(20 - x^2)
A vector normal to the sphere at point (x, y, z), obtained using the gradient, is 2 x i + 2 y j + 2 z k. This should be no surprise, since the radial vector x i + y j + z k is normal to the surface at (x, y, z); the first of these is just double the first.
Using either we will find that cos(theta) = z / sqrt(x^2 + y^2 + z^2) = sqrt(36 - x^2 - y^2) / 6, so we will integrate 6 / sqrt( 36 - x^2 - y^2) over our circle..
Alternatively we can solve the equation of the sphere for z, obtaining z = f(x, y) = sqrt( 36 - x^2 - y^2 ). In this case f_x = - x / sqrt( 36 - x^2 - y^2), f_y = - y / sqrt( 36 - x^2 - y^2), and sqrt( 1 + f_x^2 + f_y^2) = 6 / sqrt( 36 - x^2 - y^2).
We integrate the expression sqrt( 1 + f_x^2 + f_y^2) = 6 / sqrt( 36 - x^2 - y^2) over the region, obtaining
int(int(6 / sqrt( 36 - x^2 - y^2) dy, -sqrt(20 - x^2) , sqrt(20 - x^2) ) dx, -2 sqrt(5), 2 sqrt(5) ).
Self-critique (if necessary):
Self-critique rating:
Question: `q003. Find the surface area of the portion of the cylinder x^2 + z^2 = 9 which lies above the triangle with vertices (0,0,0), (1,1,0), (1,0,0).
Your solution:
Confidence rating:
Given Solution:
The cylinder has gradient vector 2 x i + 2 z k, so cos(theta) = 2 z / 2 sqrt( x^2 + z^2) = z / sqrt( x^2 + z^2) and sec(theta) = sqrt( x^2 + z^2 ) / 2 z. Since z = sqrt(9 - x^2) this simplifies to sqrt( 9 ) / ( sqrt( 9 - x^2) ). This is the function we integrate over the region.
Alternatively z = f(x,y) = sqrt( 9 - x^2) so f_x = -x / sqrt( 9 - x^2), f_y = 0 and sqrt( 1 + f_x^2 + f_y^2 ) = sqrt( 1 + x^2 / (9 - x^2) ) = sqrt( 9 / (9 - x^2) ) = 3 / sqrt( 9 - x^2 ).
Either way this function is integrated over the region 0 < x <= 1, 0 <= y <= 1 - x.
The integral is
int( int( 3 / sqrt( 9 - x^2) dy, 0, 1-x) dx, 0, 1)
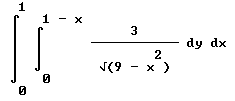
Self-critique (if necessary):
Self-critique rating: