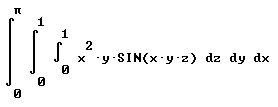
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.
Question: `q001. Compute the iterated triple integral Int( Int( Int(x^2*y sin(xyz) dz, 0,1) dy,0,1) dx,0, pi)
Your solution:
Confidence rating:
Given Solution:
The inner integrand is x^2 y sin(x y z) with respect to z. Antiderivative is -x^2 y * (cos(x y z) / x y) = x cos(x y z). Between z = 0 and z = 1 this changes from -x cos(0) to -x cos(x y), a change of x - x cos(x y).
The middle integrand is therefore x - x cos(x y), integrated with respect to y. Antiderivative is - x sin(x y) / x + x y / 2 = -sin(x y) + xy. Between y = 0 and y = 1 this changes from - sin(0) + 0 to -sin(x) + x, a change of -sin(x) + x.
The outer integrand is therefore - sin(x) + x = cos(x) + x^2 / 2. The change in the value of the antiderivative between x = 0 and x = pi is thus cos(pi) + pi^2 / 2 - cos(1) = -2 + pi^2 / 2.
In standard form the integral is written
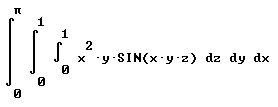
Self-critique (if necessary):
Self-critique rating:
Question: `q002. Evaluate the triple integral of xz + 2yx over D with respect to V where D is the box 2<= x <= 4, 1 <= y <= 3, -1 <= z <= 1
Your solution:
Confidence rating:
Given Solution:
The integral is
int(int(int((xz+2yx) dz, -1, 1) dy, 1, 3) dx, 2, 4)
The inner integrand is x z + 2 y x, integrated with respect to z, which gives us antiderivative x z^2 / 2 + 2 y x z. Between z = -1 and 1 this antiderivative changes from x / 2 - 2 y x to x / 2 + 2 y x = 4 y x.
The middle integrand is therefore 4 y x with respect to y, which gives us antiderivative 2 y^2 x. Between y = 1 and 3 this antiderivative changes from 2 x to 18 x, a change of 16 x.
The outer integrand 16 x is easily evaluated between x = 2 and x = 4. Antiderivative is 8 x^2, which changes from 32 to 128, a change of 96.
Self-critique (if necessary):
Self-critique rating:
Question: `q003. Use a triple integral to find the volume of the solid bounded by y = 4 - x^2, z = 0, and z = y.
Your solution:
Confidence rating:
Given Solution:
y = 4 - x^2 is a parabolic cylinder extending above and below the parabola y = 4 - x^2 in the x y plane. This parabola has vertex at (0, 4) and opens in the negative y direction, passing through the x axis at (2, 0) and (-2, 0).
The plane z = 0 is just the x y plane, and the plan z = y 'slices' 3-dimensional space at an angle of 45 degrees to the x y plane, 'cutting through' at the x axis.
The region of the cylinder above the x y plane and below the z = y plane is finite. The region above the z = y plane and below the x y plane is infinite in extent.
We integrate to find the volume of the finite region.
In the x y plane the region beneath the cylinder can be described as -2 <= x < = 2, 0 <= y <= 4 - x^2, 0 <= z <= y.
Our integral is therefore
int(int(int(dz, 0, y) dy, 0, 4 - x^2), dx, -2, 2).
Our inner integrand is just 1 with respect to z, with antiderivative z. Between z = 0 and z = y our antiderivative changes by y.
The integrand of our middle integral is therefore y, integrated with respect to y, giving us antiderivative y^2 / 2. Between y = 0 and y = 4 - x^2 this antiderivative changes by (4 - x^2)^2 / 2 = (16 - 8 x^2 + x^4) / 2 = 8 - 4 x^2 + x^4/2.
The integrand of our outer integral is therefore 8 - 4 x^2 + x^4/2, integrated with respect to x. Our antiderivative is 8 x - 4/3 x^3 + x^5 / 10. Between -2 and 2 this antiderivative changes by 2 * (16 - 4/3 * 8 + 32/10) = 256/15.
It might be instructive to contrast this with the double integral which yields the same result.
For each area increment `dA with sample point (x_hat, y_hat), the corresponding region of our solid extends from z = 0 to z = y_hat. So the volume of the region is y_hat * `dy * `dx.
The resulting Riemann sum approaches the integral int(int(y dy, 0, 4-x^2) dx, -2, 2) = 256/15.
Self-critique (if necessary):
Self-critique rating:
Question: `q004. Change the order of integration of the triple integral Int(Int(Int(f(x,y,z) dz, 0, 1-2x) dy, 0, 1-4x^2) dx, 0, 1/2) to dy dx dz.
Your solution:
Confidence rating:
Given Solution:
The region can be described by 0 <= x <= 1/2, 0 <= y <= 1 - 4 x^2, 0 <= z <= 1 - 2 x.
0 <= x <= 1/2, 0 <= y <= 1 - 4 x^2 describes the region between the x axis and the parabola y = 1 - 4 x^2. The vertex is (0, 1) and the x intercepts are (+- 1/2, 0).
This region can also be described as follows:
For any y between 0 and 1, the horizontal line through (0, y) meets the boundary curve at coordinate x, such that y = 1 - 4 x^2. The value of x is therefore x = +- sqrt( (1 - y) / 4) = +- 1/2 sqrt( 1 - y ). The horizontal line is inside the region at the point (0, y) and therefore remains inside the region between these two values of x.
The region in the x y plane can therefore be described as 0 <= y <= 1/2, -1/2 sqrt( 1 - y ) <= x <= 1/2 sqrt( 1 - y ).
...
Self-critique (if necessary):
Self-critique rating:
Question: `q005. Use triple integration to find the volume of the following solids.
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating: