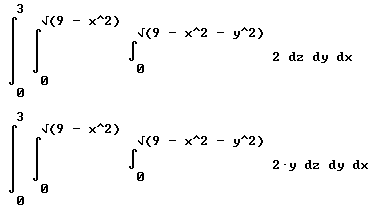
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.
Question: `q001. Find the center of mass of the part of the spherical solid with density delta = 2 described by x^2 + y^2 + z^2 <= 9, with x,y,z all >= 0.
Your solution:
Confidence rating:
Given Solution:
The region is described by 0 <= x <= 3, 0 <= y <= sqrt( 9 - x^2 ), 0 <= z <= sqrt( 9 - x^2 - y^2).
The typical volume increment has dimensions `dx by `dy by `dz, hence volume `dV = `dx * `dy * `dz. The increment includes a sample point but it is irrelevant to the mass of the integral, which is `dm = density * `dV (mass = density * volume). Since density is always 2, the mass increment is `dm = 2 * `dV = 2 * `dx * `dy * `dz.
If we form our Riemann sum, then take the limit, we find that the total mass is
int(int(int( 2 dz, 0, sqrt(9 - x^2 - y^2)) dy, 0, sqrt(9 - x^2) ) dx, 0, 3) = 9 pi.
Note:
The portion of the sphere which corresponds to this region comprises 1/8 the volume of the total sphere.
The volume of a sphere of radius 3 is 4 pi * 9 = 36 pi, so the volume of the present region is 9/2 pi. Multiplying this by the uniform density 2 gives us the total mass 9 pi.
We now find the 'torque' of the region about the x axis, for which we will use the symbol tau_x:
A typical volume increment, for which we now include a sample point (x_hat, y_hat, z_hat), lies at horizontal distance y_hat from the axis, so it contributes torque `dTau_x = y_hat * `dm = y_hat * 2 `dV = y_hat * 2 * `dx * `dy * `dz.
If we form our Riemann sum and take the limit we get the integral
tau_x = int(int(int( 2 y dz, 0, sqrt(9 - x^2 - y^2)) dy, 0, sqrt(9 - x^2) ) dx, 0, 3) = 81 pi / 8.
The center of mass therefore occurs at y coordinate
y_cMass = tau_x / mass = 81 pi / 8 / (9 pi) = 9/8.
Compare to the central point y = 1.5 between y = 0 and y = 3. If the region was an 'enclosing cube' this would be the center of mass in the y direction. However the mass of the spherical region is concentrated closer to the x axis than would the mass of the cube, and as a result the center of mass is closer to the x axis.
If we analyze the torques about the y and z axes, we get analogous results:
tau_y = int(int(int( 2 x dz, 0, sqrt(9 - x^2 - y^2)) dy, 0, sqrt(9 - x^2) ) dx, 0, 3) = 81 pi / 8
tau_z = int(int(int( 2 x dz, 0, sqrt(9 - x^2 - y^2)) dy, 0, sqrt(9 - x^2) ) dx, 0, 3) = 81 pi / 8
each of which divided by the mass again yields the same result 9/8.
We conclude that the center of mass is (9/8, 9/8, 9/8).
Some of the integrals look like this:
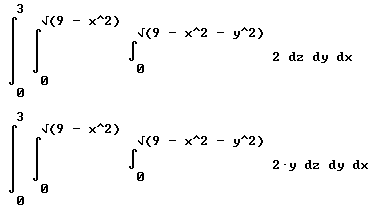
Self-critique (if necessary):
Self-critique rating:
Question: `q002. Use double integration to find the center of mass when delta(x,y) = y over the region bounded by y = e^-x, x = 0, x = 3, y = 0.
Your solution:
Confidence rating:
Given Solution:
The region is described by
0 <= x <= 3, 0 <= y <= e^(-x).
The mass increment has area `dy by `dx and density delta(x_hat, y_hat) = y_hat is `dm = y_hat * `dy * `dx, leading in the usual manner to the integral
int(int( y dy, 0, e^(-x))dx, 0, 3) = .249, approximately.
The moment (or torque) of a mass increment about the x axis is y_hat `dm = y_hat * (y_hat * `dy * `dx) = y_hat^2 `dy `dx, leading to the integral
tau_x = int(int( y ^2 dy, 0, e^(-x))dx, 0, 3) = .111.
The moment (or torque) of a mass increment about the y axis is x_hat `dm = x_hat * (y_hat * `dy * `dx), leading to the integral
tau_y = int(int( x y dy, 0, e^(-x))dx, 0, 3) = .122.
The coordinates of the center are therefore
x_cMass = tau_y / mass = .122 / .249 = .49, roughly, and
y_cMass = tau_x / mass = .111 / .249 = .45, roughly.
Standard-form representation of these integrals:
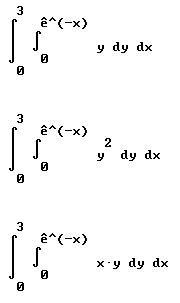
Self-critique (if necessary):
Self-critique rating:
Question: `q003. Find I_x, the moment of inertia about the x-axis, of the lamina that covers the region bounded by the graph of y = 3 - x^2 and the x-axis, and with density delta(x,y) = x^2*y^2.
Your solution:
Confidence rating:
Given Solution:
The typical area increment has dimensions `dy by `dx and sample point (x_hat, y_hat). The mass of the region is `dm = density * area = x_hat^2 y^hat^2 `dx `dy, and its distance from the x axis is r = y_hat. Its moment of inertia is mass * r^2, giving us `dI = `dm * r^2 = (x_hat^2 y^hat^2 `dx `dy) * y_hat^2 = x_hat^2 y^hat^4 `dx `dy. This leads us to the integral
int(int(x^2 y^4 dy, 0, 3 - x^2) dx, -sqrt(3), sqrt(3) ) = 14.35, approx..
This is reasonable. This region of the graph covers most of an 'enclosing rectangle' with dimensions 2 sqrt(3) * 3 = 10, very approximately. (1, 1) could be regarded as a 'typical point', at which density is 1 and distance from the x axis is 1, so the moment of inertia of a neighboring region would be is about 1 * area. Extending this to the entire region would result in moment of inertia 1 * 10 = 10, which puts our much more accurate answer of 14.35 in the right ballpark.
Self-critique (if necessary):
Self-critique rating:
Question: `q004. Suppose the joint probability density function for the random variables X and Y is f(x,y) = {4e^(-2x)*e^(-y) if x,y >= 0, 0 otherwise.} Find the probability that X + Y <= 1.
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question: `q005. Find the average value of the function f(x,y,z) = x + 2y + 3z over the solid region S bounded by the tetrahedron with vertices (0,0,0), (1,0,0), (0,1,0), (0,0,1).
Your solution:
Confidence rating:
Given Solution:
GOOD STUDENT SOLUTION FOR INTEGRAL OF FUNCTION OVER REGION:
Tetrahedron: first octant that lies beneath the plane x+y+z=1
=[Int(Int(Int x+2y+3z dz, 0, 1-x-y), dy, 0, 1-x), dx, 0, 1]
=Int (x+2y+3z dz, 0, 1-x-y)
=[(x+y-1)*(x-y-3)]/2
=Int ([(x+y-1)*(x-y-3)]/2 dy, 0, 1-x)
=[-(x-1)^2*(2x-5)]/6
=Int ([-(x-1)^2*(2x-5)]/6 dx, 0, 1)
=1/4
#$&*
INSTRUCTOR'S SUPPLEMENT:
That is the correct integral for the function.
The average value of the function is the integral, divided by the volume.
The volume is 1/6 (this could be obtained by integrating the volume increment over the given region).
The average value of the function is therefore 1/4 / (1/6) = 3/2.
There are a number of ways to think about this result.
First, does it make common sense?
x + 2y + 3z is equal to 0 at (0, 0, 0), to 1 at (1, 0, 0), to 2 at (0, 1, 0), and to 3 at (0, 0, 1).
The largest cross-section is in the x-y plane; for the region 0 <= x <= 1, 0 <= y <= 1 - x we have x + y <= 1.
The greatest values of f(x, y, z) occur near the 'tips' of the tetrahedron, which don't occupy a lot of volume.
So an average value of 1.5 seems to be in the right general range.
Second, how can we understand the meaning of the average value?
If f(x, y, z) is interpreted as a mass density, our first integral tells us that the mass of the tetrahedron is 1/4 and our second integral gives us volume 1/6. Since average density = mass / volume, our result 1/4 / (1/6) = 3/2 = 1.5 gives us the average density of the object.
</h3>
Self-critique (if necessary):
Self-critique rating: