If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution.† If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it.† This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
014. Tangent Lines and Tangent Line Approximations
Question: `q001. What are the coordinates of the x = 5 point and the slope at that point of the graph of the function y = .3 x^2?
What is the equation of the line through the point and having that slope?
Sketch the line and the curve between x = 3 and x = 7 and describe your sketch.
How close, in the vertical direction, is the line to the graph of the y = .3 x^2 function when x = 5.5, 6, 6.5 and 7?
Your solution:
Confidence Assessment:
Given Solution:
`aThe x = 5 point has y coordinate y = .3 * 5^2 = 7.5, so the point lies at (5, 7.5).
The slope that that point is found by evaluating the derivative at that point. The derivative is y ' = .6 x, so the slope is y ' = .6 * 5 = 3.
The line therefore passes through the point (5,7.5) and has slope 3. Its equation is therefore y - 7.5 = 3 ( x - 5), which simplifies to y = 3 x - 7.5.
When x = 5.5, 6, 6.5 and 7, the y coordinates of the line are
y = 3 ( 5.5 ) - 7.5 = 9,
y = 3 (6) -7.5 = 10.5,
y = 3 (6.5) -7.5 = 12,
y = 3 (7) -7.5 = 13.5.
At the same x coordinates the function y =.3 x ^ 2 takes values
y = .3 (5.5) ^ 2 = 9.075,
y =.3 (6) ^ 2 = 10.8,
y =.3 (6.5) ^ 2 = 12.675, and
y =.3 (7) ^ 2 = 14.7.
The straight line is therefore lower than the curve by
9.075 - 9 = .075 units when x = 5.5,
10.8-10.5 = .3 when x = 6,
12.675-12 = .675 when x = 6.5, and
14.7-13.5 = 1.2 when x = 7.
We see that as we move away from the common point (5,7.5), the line moves away from the curve more and more rapidly.
Your sketch should show a straight line tangent to the parabolic curve y =.3 x^2, with the curve always above the line except that the point tangency, and moving more and more rapidly away from the line the further is removed from the point (5,7.5).
The line you have drawn is called the line tangent to the curve at the point (5,7.5).
Self-critique (if necessary):
Self-critique Rating:
Question: `q002. What is the equation of the line tangent to the curve y = 120 e^(-.02 t) at the t = 40 point?
If we follow the tangent line instead of the curve, what will be the y coordinate at t = 40.3?
How close will this be to the y value predicted by the original function?
Will the tangent line be closer than this or further from the original function at t = 41.2?
Your solution:
Confidence Assessment:
Given Solution:
`aThe tangent line at the x = 40 point will have y coordinate y = 120 e^(-.02 * 40) = 53.9194, accurate to six significant figures. The derivative of the function is y ' = -2.4 e^(-.02 t) and at x = 40 has value y ' = -2.4 e^(-.02 * 40) = -1.07838, accurate to six significant figures.
The tangent line will therefore pass through the point (40, 53.9194) and will have slope 1.07838. Its equation will therefore be
y - 53.9194 = -1.07838 ( x - 40), which we can solve for y to obtain
y = -1.07838 x + 97.0546.
The values of the function at x = 40.3 and x = 41.2 are 53.5969 and 52.6408.
The y values corresponding to the tangent line are 53.5958 and 52.6253. We see that the tangent line at x = 40.3 is .0011 units lower than the curve of the function, and at x = 41.2 the tangent line is .0155 units lower--about 14 times as far from the curve as at the x = 40.3 point.
STUDENT QUESTION
I know that the derivitave of e^x is
e^x, but what happened to the 120? Why did it become -2.4?
INSTRUCTOR RESPONSE
e^(-.02 t) is a composite function f(g(t)),
with g(t) = -.02 t and f(z) = e^z.
g ' (t) = -.02.
f ' (z) = e^z
So g ' (t) * f ' ( g ( t) ) = -.02 * e^(-.02 t).
Multiply this by 120 and you have y ' = -2.4 e^(-.02 t).
Self-critique (if necessary):
Self-critique Rating:
Question: `q003. Sketch a graph of this curve and the t = 40 tangent line and describe how the closeness of the tangent line to the curve changes as we move away from the t = 40 point.
Your solution:
Confidence Assessment:
Given Solution:
`aYour sketch should show the gradually curving exponential function very close to the tangent line. The tangent line is straight while the slope of the exponential function is always increasing. At the t = 40 point the two meet for an instant, but as we move both to the right and to the left the exponential curve moves away from the tangent line, moving away very gradually at first and then with increasing rapidity.
STUDENT QUESTION
For some reason Iím having trouble understanding this. I
tried putting the y = 120 e^(-.02t) function into my
calculator and it wouldnít show up. I can see the tangent line, but what do I
compare it to?
INSTRUCTOR RESPONSE
Prerequisite courses, and in the early review assignments in this course, should provide sufficient understanding of exponential functions to reason this out without relying on a calculator to construct the graph.
The function y = 120 e^(-.02 t) goes through the point (0,
120), and decreases at a decreasing rate with the positive x axis as a
horizontal asymptote.
Being an exponential function it has a constant 'half-life' found by setting
e^(-.02 t) equal to 1/2 and solving for t, obtaining approximately t = 35.
So around t = 35 the y value will have decreased from its t = 0 value of 120 to half that, giving us the approximate point (35, 60).
By the time t has changed by another 35 its value will have again decreased to half, giving us the approximate point (70, 30)
The graph continues to decrease in a similar manner toward its asymptote with the positive x axis.
An alternative way to construct the graph would be to find the point where -.02
t = -1, which occurs when t = 50.
At this point the y value is e^-1 = 1 / e, which lies between 1/2 and 1/3 (closer to 1/3).
So the graph of this function decreases from y = 120 at t = 0 to a y value between 1/2 * 120 = 60 and 1/3 * 120 = 40, closer to 40. A reasonable estimate would be 45, giving us the estimated point (50, 45).
This gives you a basis for constructing an approximate graph.
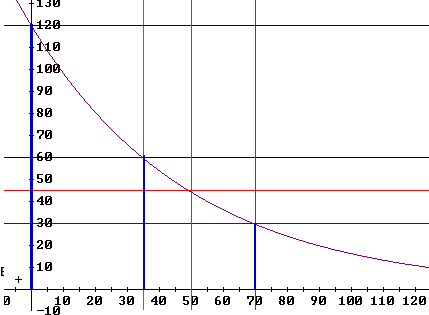
The figure below shows the graph, along with the lines x = 35, x = 70, y = 120, y = 70 and y = 30. The vertical blue line segments depict the halving of the y values every time x changes by 35. The lines x = 50 and y = 45 are also depicted.
As we have seen the point (40, 53.9194) lies on the graph, and this is consistent with the basic sketch of the exponential, constructed as above or by any reasonable means. We also know that the slope at this point is about -1.08, which is also consistent with a reasonable sketch of the graph.
The figure below depicts the lines x = 40 and y = 53.9, as well as the tangent line.
In any case, while you shouldn't depend on the calculator for
this type of graphing, the calculator can be a valuable tool and you
should also know how to deal with this function with
your calculator. Can you tell me what calculator you used, and what steps you
went through in trying to get the information from your calculator?
Self-critique (if necessary):
Self-critique Rating:
Question: `q004. What is the equation of the line tangent to the curve y = 20 ln( 5 x ) at the x = 90 point?
Your solution:
Confidence Assessment:
Given Solution:
`aAt x = 90, we have y = 20 ln (5 * 90) = 20 ln(450) = 20 * 6.1 = 122, approx..
So we are looking for a straight line through the point (90, 126). The slope of this straight line should be equal to the derivative of y = 20 ln(5 x) at x = 90.
The derivative of ln(5x) is, by the chain rule, (5x) ' * 1 / (5x) = 5 / (5x) = 1/x. So y ' = 20 * 1 / x = 20 / x.
At x = 90 then we have y ' = 20 / 90 = .22, approx.. Thus the tangent line passes through (90, 122) and has slope .22. The equation of this line is
( y - 122 ) / (x - 90) = .22, which is easily rearranged to the form
y = .22 x + 102.
Self-critique (if necessary):
Self-critique Rating:
Question: `q005. Using the tangent line and the value of the function at x = 3, estimate the value of f(x) = x^5 and x = 3.1. Compare with the actual value.
Your solution:
Confidence Assessment:
Given Solution:
`af ' (x) = 5 x^4. When x = 3, f(x) = 3^5 = 243 and f ' (x) = 5 * 3^4 = 405.
Thus tangent line passes through (3, 243) and has slope 405. Its equation is therefore
(y - 243) / (x - 3) = 405, which simplifies to
y = 405 x - 972.
This function could be evaluated at x = 3.1. However a more direct approach simply uses the differential.
In this approach we note that at x = 3 the derivative, which gives the slope of the tangent line, is 405. This means that between (3, 243) and the x = 3.1 point the rise/run ratio should be close to 405. The run from x = 3 to x = 3.1 is 1, so a slope of 405 therefore implies a rise equal to slope * run = 40.5.
A rise of about 40.5 means that y = 3.1^5 should change by about 40.5, from 243 to about 283.5.
The actual value of 3.1^5 is about 286.3. The discrepancy between the straight-line approximation and the actual value is due to the fact that y = x^5 is concave up, meaning that the slope is actually increasing.
The closely-related idea of the differential, which will be developed more fully in the next section, is that if we know the rate at which the function is changing at a given point, we can use this rate to estimate its change as we move to nearby points.
Self-critique (if necessary):
Self-critique Rating:
Question: `q006. Using the differential and the value of the function at x = e, estimate the value of ln(2.8). Compare with the actual value.
Your solution:
Confidence Assessment:
Given Solution:
`aAt x = e we have ln(x) = ln(e) = 1 (this is because of the definition of the natural log function as the inverse of the exponential function).
The derivative of ln(x) is 1/x, so at x = e the rate at which financial log function is changing is 1 / e.
Since e = 2.718, approx., between x = e and x = 2.8, the value of x changes by about 2.8 - 2.718 = .082. Since the rate at which y is changing in this vicinity remains close to the value x = 1/e of the derivative, the change in y is approximately
`dy = rate * `dx = 1/e * .082 = .082 / 2.718 = .030.
Thus at x = 2.8, y = ln(x) takes value approximately 1 + .030 = 1.030.
The actual value of ln(2.8) to six significant figures is 1.02961, which when rounded off to four significant figures is equal to our approximate value y = 1.030.
STUDENT COMMENT:
This is definitely something I need to study on. I have to admit I'm slightly lost. Is this normal?
INSTRUCTOR RESPONSE
The differential is a new concept, very
important but not always easy at first encounter.
So it's well worth thinking about. The more you think about it now, the more
likely you'll understand it later (e.g., when you encounter it in your text).
The reason it's covered here is so when you encounter it in your text, it won't
be your first time.
STUDENT COMMENT:
I was confused around the first part of
this equation until I got down to how to get to .030. Also, why do we add 1?
INSTRUCTOR RESPONSE
(2.8-2.718) is `dx, the change in x from the x = e 'reference point' to the x = 2.8 point.
.368 is the rate at which y changes with respect to x.
When we multiply the average rate at which y changes with respect to x by `dx,
the change in x, we get `dy, which is the change in y.
The calculation isn't exact, because the rate changes a bit over the interval;
however since the interval is short the rate doesn't change by much, and the
approximation is very good.
To get the new value of y we add the change in y to the original value of y;
i.e., we add the .030 to the original y value 1.
STUDENT QUESTION
I understand why we find the difference in x1 and x2 since we are not given an equation for y.
Still as the student above I donít understand the method of adding 1 to get the
y value.
INSTRUCTOR RESPONSE:
ln(e) = 1, which is where the 1 comes
from.
The slope at the point (e, 1) is 1/e = .367, approx.
The 'run' from x = e to x = 2.8 is .082. So the 'rise' is slope * run = .367 *
.082 = .030.
From (e, 1) a 'run' of .082 and a 'rise' of .030 takes us to the point (2.8,
1.030).
So our approximate value of y at x = 2.8 is 1.030.</h3>
STUDENT NOTE
I think I understand the first
part of this problen but I get what is going on until we use the differential. I
understand
that the differential is dy/dx=rate and I see were the rate came from the
derivative fo the original expression but what I do
not get is were did the value we used for DX come from?????????
INSTRUCTOR RESPONSE
Note that to start with, you don't assume that ln(2.8) = 1.03. This is what you are asked to find using the differential approximation. Your approximation will be based on the point (e, 1) and the slope .367 (approx).
So you are basing the approximation on
the value of ln(x) at e. You know that the slope at this point is 1/e,
approximately
.367. You want the value of the function ln(x) at x = 2.8.
Starting from the point (e, 1) = (2.718, 1), approx., you follow a straight line
with slope about .367 until your x
coordinate is 2.8.
The necessary 'run' is from 2.718 to 2.8, a distance of about .082. (This is where you get the value of `dx)
The 'rise' is therefore rise = slope * run = .367 * .082 = .030, approx..
So, starting from (e, 1) you move .082 units in the x direction and .030 units in the y direction, ending up at the approximate point (2.8, 1.03).
The tangent line is very close to the graph, so you conclude that ln(2.8) = 1.03, approx..
STUDENT COMMENT
I really had no idea how to approach
this problem. I am assuming that differential means derivative. I tried to
compute the actual value and donít really know how to estimate it.
INSTRUCTOR RESPONSE
<h3>@&
The differential is
df = f'(x) dx
where dx is the change in the x coordinate and df is the approximate
corresponding change in the value of the function.
A differential approximation will start with a known value of the function at
some value of x, and find the approximate change df in the value of the function
between that value of x and a new value of x. dx is the change in x between the
value at which f is known, and the new value.
Since f ' (x) is the rate of change of f(x), equivalent to the slope of the
graph, and dx is the 'run' between the two values of x, f ' (x) dx is the
product of the slope and the run, which gives you the 'rise'. The 'rise' is the
approximate change in f, i.e., df.
*@</h3>
You are working with the function y = ln(x). The derivative
of this function is
y ' = 1 / x.
When x = e, we get
y ' = 1 / e.
When x = 2.8, y ' = 1 / 2.8 but that's not relevant to this approximation.
A numerical approximation of 1 / e is .368.
The value of y = ln(x), when x = e, is 1, since the ln(x) and e^x functions are
inverse functions.
So the graph of y = ln(x), at the point where x = e, contains the point (e, 1),
approximately (2.718, 1).
The slope of the graph of the tangent line at that point is .368, the value of
the derivative function when x = e = 2.718 (approx.)..
The slope of the tangent line is therefore .368. To get from x = e to x = 2.8,
the value x has to change by about .082. Thus, between the x = e and x = 2.8
point, the 'run' is .082.
From the run and the slope, you find the rise, which is the change in the value
of y.
Self-critique (if necessary):
Self-critique Rating:
Question: `q007. Using the tangent line verify that the square root of a number close to 1 is twice as close to 1 as the number. Hint: Find the tangent line approximation for the function f(x) = `sqrt(x) at an appropriate point.
Your solution:
Confidence Assessment:
Given Solution:
`aThe function f(x) = `sqrt(x) takes value 1 when x = 1. The derivative of f(x) = `sqrt(x) is 1 / ( 2 * `sqrt(x) ), which takes value 1/2 when x = 1.
The tangent-line approximation to f(x) is therefore a straight line through (1, 1) having slope 1/2. This line has equation (y - 1) / (x - 1) = 1/2, or y = 1/2 ( x - 1) + 1.
This number differs from 1 by 1/2 (x-1), which is half the difference between 1 and x. This approximation works for x values near 1.
Thus if x is close to 1, then y is approximately twice as close to 1 as is x.
STUDENT QUESTION
I still donít think I quite
understand this concept.
INSTRUCTOR RESPONSE
f(1) = 1
If x is close to 1 then
The proximity of x to 1 is | x - 1 |
(e.g., 1.07 lies | 1.07 - 1 | = .07 units from 1; or .95 lies | .95 - 1 | =
.05 units from 1).
That is, x is within distance x - 1 of 1.
If x is close to 1 then the tangent-line approximation is
sqrt(x) = 1/2 (x - 1) + 1.
The proximity of this number to 1 is | (1/2 ( x-1) + 1) - 1 | = 1/2 | x - 1|
e.g., sqrt(1.07) = 1/2 (1.07 - 1) + 1 = 1/2 (.07) + 1 = 1.035, which is twice as close to 1 as 1.07
for x = 1.07 we have 1/2 | x - 1| = 1/2 (.07) = .035.
STUDENT QUESTION
I do not understand question asked. Even after looking at solution I understand everything except how you obtained derivative for sqrt(x)
INSTRUCTOR RESPONSE
sqrt(x) = x^(1/2), a power function.
Its derivative is 1/2 x^(1/2 - 1) = 1/2 x^(-1/2) = 1/2 * 1/sqrt(x), or 1 / (2
sqrt(x)).
At x = 1 the derivative is 1/2, so the tangent-line approximation is a straight line through (1, 1) with slope 1/2.
STUDENT COMMENT
I see where my problem is nowÖ
when I saw twice I assumed that it meant that if one value was 1 the other
should be 2 I now
see that it means twice as close to the value of one example being that if x is
.9 in my equation then y will be .95 so it is
half as far away from one as my original x value. Does it sound like I get this
now that I have read the question
correctly?
INSTRUCTOR RESPONSE
Good statement. It appears that you do now understand the question.
Self-critique (if necessary):
Self-critique Rating:
Question: `q008. Using the tangent line approximaton verify that the square of a number close to 1 is twice as far from 1 as the number.
Your solution:
Confidence Assessment:
Given Solution:
`aThe tangent-line approximation to f(x) = x^2, near x = 1, is y = 2(x-1) + 1. This number is twice as far from 1 as is x.
STUDENT COMMENT: I am not really understanding this part. INSTRUCTOR RESPONSE: *&*& You should understand the part about the tangent-line approximation near x = 1 being y = 2(x-1) + 1.
Graph y = 2(x-1) + 1. If you move horizontally over from the point (1, 1) you are changing x. If you then move vertically up to the graph from this point you will find the change in y. For this function that change will be double the change in x. *&*&.
STUDENT COMMENT:
Why are these tangent line
approximations so hard? Why did you start with x^2?
INSTRUCTOR RESPONSE
They aren't that bad once you sort out
what they mean. It's the sorting out that can be a challenge. When you see this
again in your text, you'll have a good start and also a good reference to make
sense of it. The reason I introduce the important ideas in the qa before you see
them in the text is that it makes the text easier to understand, so if you
didn't master it here it will be easier to master at that point.
We start with x^2 because the question asks about the square of a number.