If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
023. `query 23
Question: `qQuery problem 2.
Describe the sum of the two graphs.
Your solution:
Confidence Assessment:
Given Solution:
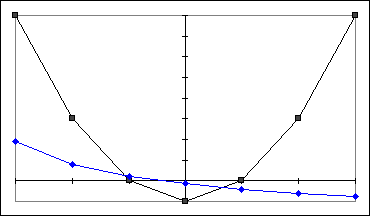
`a** The 'black' graph takes values 8, 3, 0, -1, 0, 3, 8 at x = -3, -2, -1, 0, 1, 2, 3.
The 'blue' graph takes approximate values 1.7, .8, .2, -.1, -.4, -.6, -.8 at the same x values.
The 'blue' graph takes value zero at approximately x = -.4.
The sum of the two graphs will coincide with the 'blue' graph where the 'black' graph is zero, which occurs at x = -1 and x
= 1.
The sum will coincide with the 'black' graph where the 'blue' graph is zero, which occurs at about x = -.4. **
STUDENT QUESTION:
I don't understand where you are getting these numbers.
INSTRUCTOR RESPONSE: The graph in the stated problem appears below. The x and y scales are marked in units. You should begin by orienting yourself to these graphs: convince yourself that the points marked on the graphs have the coordinates quoted in the given solution.
Self-critique (if necessary):
Self-critique rating:
Question: `qWhere it is the sum graph higher than the 'black' graph, and where is it lower? Answer by giving specific intervals.
Your solution:
Confidence Assessment:
Given Solution:
`a** The sum of the graphs is higher than the 'black' graph where the 'blue' graph is positive, lower where the 'blue' graph
is negative.
The 'blue' graph is positive on the interval from x = -3 to x = -.4, approx.. This interval can be written [-3, -.4), or -3 <=
x < -.4. **
Self-critique (if necessary):
Self-critique rating:
Question: `qWhere it is the sum graph higher than the 'blue' graph, and where is it lower? Answer by giving
specific intervals.
Your solution:
Confidence Assessment:
Given Solution:
`a** The sum of the graphs is higher than the 'blue' graph where the 'black' graph is positive, lower where the 'black'
graph is negative.
The 'black' graph is positive on the interval from x = -1 to x = 1, not including the endpoints of the interval. This interval
can be written (-1, 1) or -1 < x < 1. **
Self-critique (if necessary):
Self-critique rating:
Question: `qWhere does thus sum graph coincide with the 'black' graph, and why? Give your estimate of the
specific coordinates of the point or points where this occurs.
Your solution:
Confidence Assessment:
Given Solution:
`a** The sum coincides with the 'black' graph where the 'blue' graph is zero, which occurs at about x = -.4. The
coordinates would be about (-.4, -.7), on the 'black' graph. **
Self-critique (if necessary):
Self-critique rating:
Question: `qWhere does thus sum graph coincide with the 'blue' graph, and why? Give your estimate of the
specific coordinates of the point or points where this occurs.
Your solution:
Confidence Assessment:
Given Solution:
`a** The sum coincides with the 'blue' graph where the 'black' graph is zero, which occurs at x = -1 and x = 1. The
coordinates would be about (-1, .2) and (1, -.4), on the 'blue' graph. **
Self-critique (if necessary):
Self-critique rating:
Question: `qQuery problem 3
Describe the quotient graph obtained by dividing the 'black' graph by the 'blue' graph. You should answer the following
questions:
Where it is the quotient graph further from the x axis than the 'black' graph, and where is it closer? Answer by giving
specific intervals, and explaining why you believe these to be the correct intervals.
Where it is the quotient graph on the same side of the x axis as the 'black' graph, and where is it on the opposite side,
and why? Answer by giving specific intervals.
Where does thus quotient graph coincide with the 'black' graph, and why? Give your estimate of the specific coordinates
of the point or points where this occurs.
Where does the quotient graph have vertical asymptote(s), and why? Describe the graph at each vertical asymptote.
Your solution:
Confidence Assessment:
Given Solution:
`a** The 'black' graph is periodic, passing through 0 at approximately x = -3.1, 0, 3.1, 6.3. This graph has peaks with y
= 1.5, approx., at x = 1.6 and 7.8, approx., and valleys with y = -1.5 at x = -1.6 and x = 4.7 approx.
The 'blue' graph appears to be parabolic, passing thru the y axis at x = -1 and reaching a minimum value around y = -1.1
somewhere near x = 1. This graph passes thru the x axis at x = 5.5, approx., and first exceeds y = 1 around x = 7.5.
The quotient will be further from the x axis than the 'black' graph wherever the 'blue' graph is within 1 unit of the origin,
since division by a number whose magnitude is less than 1 gives a result whose magnitude is greater than the number being
divided. This will occur to the left of x = 1, and between about x = 2 and x = 7.5.
Between about x = 0 and x = 1 the 'blue' graph is more than 1 unit from the x axis and the quotient graph will be closer to
the x axis than the 'black' graph. The same is true for x > 7.5, approx..
The 'black' graph is zero at or near x = -3.1, 0, 3.1, 6.3. At both of these points the 'blue' graph is nonzero so the
quotient will be zero.
The 'blue' graph is negative for x < 5.5, approx.. Since division by a negative number gives us the opposite sign as the
number being divided, on this interval the quotient graph will be on the opposite side of the x axis from the 'black' graph.
The 'blue' graph is positive for x > 5.5, approx.. Since division by a positive number gives us the same sign as the number
being divided, on this interval the quotient graph will be on the same side of the x axis as the 'black' graph.
The quotient graph will therefore start at the left with positive y values, about 3 times as far from the x axis as the 'black'
graph (this since the value of the 'blue' graph is about -1/3, and division by -1/3 reverses the sign and gives us a result with
3 times the magnitude of the divisor).
The quotient graph will have y value about 2.5 at x = -1.6, where the 'black' graph 'peaks', but the quotient graph will
'peak' slightly to the left of this point due to the increasing magnitude of the 'blue' graph.
The quotient graph will then reach y = 0 / (-1) = 0 at x = 0 and, since the 'black' graph then becomes positive while the
'blue' graph remains negative, the quotient graph will become negative.
Between x = 0 and x = 2 the magnitude of the 'blue' graph is a little greater than 1, so the quotient graph will be a little
closer to the x axis than the 'black' graph (while remaining on the other side of the x axis).
At x = 3.1 approx. the 'black graph is again zero, so the quotient graph will meet the x axis at this point.
Past x = 3.1 the quotient graph will become positive, since the signs of both graphs are negative. As we approach x =
5.5, where the value of the 'blue' graph is zero, the quotient will increase more and more rapidly in magnitude (this since
the result of dividing a negative number by a negative number near zero is a large positive number, larger the closer the
divisor is to zero). The result will be a vertical asymptote at x = 5.5, with the y value approaching +infinity as x
approaches 5.5 from the left.
Just past x = 5.5 the 'blue' values become positive. Dividing a negative number by a positive number near zero results in a
very large negative value, so that on this side of x = 5.5 the asymptote will rise up from -infinity.
The quotient graph passes through the x axis near x = 6.3, where the 'black' graph is again zero. To the right of this point
both graphs have positive values and the quotient graph will be positive.
Around x = 7.5, where the 'blue' value is 1, the graph will coincide with the 'black' graph, giving us a point near (7.5, 1.3).
Past this point the 'blue' value is greater than 1 so that the quotient graph will become nearer the x axis than the 'black'
graph, increasingly so as x (and hence the 'blue' value) increases. This will result in a 'peak' of the quotient graph
somewhere around x = 7.5, a bit to the left of the peak of the 'black' graph. **
Self-critique (if necessary):
Self-critique rating:
Question: `qQuery problems 7-8
Sketch the graph of y = x^2 - 2 x^4 by first sketching the graphs of y = x^2 and y = -2 x^4.
How does the result compare to the graph of y = x^2 - x^4, and how do you explain the difference?
Your solution:
Confidence Assessment:
Given Solution:
`a** At x = 0, 1/2, 1 and 2 we have x^2 values 0, 1/4, 1 and 4, while -x^4 takes values 0, -1/16, -1 and -16, and -2
x^4 takes values 0, -1/8, -2 and -32.
All graphs clearly pass through the origin.
The graphs of y = x^2 - x^4 and y = x^4 - 2 x^4 are both increasingly negative at far right and far left.
Graphical addition will show that y = x^2 - x^4 takes value 0 and hence passes thru the x axis when the graphs have
equal but opposite y values, which occurs at x = 1 and x = -1. To the left of x = -1 and to the right of x = 1 the negative
values of -x^4 overwhelm the positive values of x^2 and the sum graph will be increasingly negative, with values
dominated by -x^4. Near x = 0 the graph of y = -x^4 is 'flatter' than that of y = x^2 and the x^2 values win out, making
the sum graph positive.
y = x^2 - 2 x^4 will take value 0 where the graphs are equal and opposite in value; this occurs somewhere between x =
.8 and x = .9, and also between x = -.9 and x = -.8, which places the zeros closer to the y axis than those of the graph of
y = x^2 - x^4. The graph of y = -2 x^4 is still flatter near x = 0 than the graph of y = x^2, but not as flat as the graph of
y = -x^4, so while the sum graph will be positive between the zeros the values won't be as great. Outside the zeros the
sum graph will be increasingly negative, with values dominated by -2x^4. **
The graphs you constructed, based on the basic points and behaviors of the functions y = x^2, y = -x^4 and y = -2 x^4, should have had the same characteristics and basic properties of those in the series of figures below:
The figure below depicts the graphs of y = x^2 and y = -x^4, with x and y gridlines at unit intervals.
The graph of y = x^2 - x^4 is superimposed below:
The figure below depicts the graphs of y = x^2, y = -2 x^4 and y = x^2 - 2 x^4:
The graphs of y = x^2 - x^4 and y = x^2 - 2 x^4 are depicted below:
Self-critique (if necessary):
Self-critique rating:
Question: `qHow does the shape of the graph change when you add x to get y = -2 x^4 + x^2 + x, and how
do you explain this change?
Your solution:
Confidence Assessment:
Given Solution:
`a** At x = 0 there is no change in the y value, so the graph still passes through (0, 0).
As x increases through positive numbers we will have to increase the y values of y = x^2 -2 x^4 by greater and greater
amounts. So it will take a little longer for the negative values of -2 x^4 to 'overwhelm' the positive values of x^2 + x than
to overcome the positive values of x^2 and the x intercept will shift a bit to the right.
As we move away from x = 0 through negative values of x we will find that the positive effect of y = x^2 is immediately
overcome by the negative values of y = x, so there is no x intercept to the left of x = 0.
The graph in fact stays fairly close to the graph of y = x near (0, 0), gradually moving away from that graph as the values
of x^2 and -2 x^4 become more and more significant. **
The graphs you constructed, based on the basic points and behaviors of the functions y = x^2, y = -x^4 and y = -2 x^4, should have had the same characteristics and basic properties of those in the series of figures below:
The figure below depicts the graphs of y = x^2 and y = -x^4, with x and y gridlines at unit intervals.
The graph of y = x^2 - x^4 is superimposed below:
The figure below depicts the graphs of y = x^2, y = -2 x^4 and y = x^2 - 2 x^4:
The graphs of y = x^2 - x^4 and y = x^2 - 2 x^4 are depicted below:
Self-critique (if necessary):
Self-critique rating:
If you understand the assignment and were able to solve the previously given problems from your worksheets, you should be able to complete most of the following problems quickly and easily. If you experience difficulty with some of these problems, you will be given notes and we will work to resolve difficulties.
Question: The graphs of two linear functions are depicted below. The first function f(x) has x-intercept (-8/3, 0) and y-intercept (0, 4), while the second function g(x) has y-intercept (0, 1) and slope -1/2.
You could easily find the formulas for these two functions and answer subsequent questions using these formulas, but don't do that. The task here, as you have seen, is to be able to construct graphs of combinations of functions. The purpose is to give you a deeper understanding of such functions and enhance your ability to think about and visualize complex trends.
Construct an approximate graph of the sum of these two functions.
At what approximate x coordinate do you estimate your graph of the sum intercepts the x axis?
Construct an approximate graph of the difference function f(x) - g(x).
At what approximate x coordinate do you estimate your graph of the difference function intercepts the x axis?
Your solution:
Confidence Assessment:
Question: For the graphs of the preceding, sketch the graph of the product function f(x) * g(x).
On what interval(s) is the graph of the product function positive, and on what intervals negative?
How could you have determined these intervals, based on the given graphs, without actually having sketched the graph of the product function?
On what interval(s) is the graph of the product function increasing, and on what intervals decreasing?
For large negative x, is the product function positive or negative, and how could you tell by just looking at the graphs of f(x) and g(x)?
Your solution:
Confidence Assessment:
Question: For the same functions f(x) and g(x), sketch the graph of the quotient function f(x) / g(x).
Describe all vertical and horizontal asymptotes of your graph.
On what intervals is your graph positive, and on what intervals negative?
How could you have answered this question by just looking at the graphs of the two functions?
Given just the graphs of the two functions, how would you determine whether
and where the given quotient function has one or more vertical asymptotes?
Your solution:
Confidence Assessment:
Question: In the graph below the linear function is f(x), the nonlinear function g(x).
Think about the graphs of the functions f(x) + g(x), f(x) * g(x) and f(x) / g(x).
What will be the x intercepts of each of these functions?
On what intervals will each function be positive?
What will be the sign of each of these functions for large positive x, and for large negative x?
What will be the horizontal and vertical asymptotes of the quotient function?
Describe the behavior of the quotient function near each of its vertical asymptotes.
Your solution:
Confidence Assessment:
Self-critique rating: