First night problems.
Rework these questions. Include good explanations of the details of your work.
1. Sketch a circle. Then sketch a straight line, part of which lies inside the circle. Into how many separate regions does the line divide the circle?
What is the minimum number of regions into which the circle could be divided by sketching another straight line, part of which lies inside the circle?
What is the maximum number of regions into which the circle could be divided by sketching sketch another straight line, part of which lies inside the circle?
What is the maximum number of regions into which the circle could be divided by four such straight lines?Suppose you had the circle divided into the maximum number of subregions possible when using 30 lines. What is the maximum possible number of additional regions you could get if you added another line? What is the minimum?
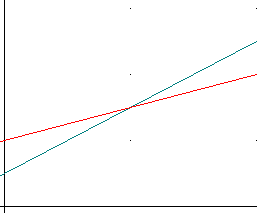
2. Two squirrels are gathering nuts. Each straight line in the graph below represents the number of nuts each squirrel has stored vs. the time since dawn. So the y coordinate of a point on a graph represents the number of nuts, and the x coordinate represents how much time has passed.
Use this graph to construct a graph of the total number of nuts stored by the two squirrels, vs. the time since dawn.
The graphs below include the two graphs above, plus four more graphs. One of the four new graphs is the correct answer to the above question. Which is it, and why?
Using your ruler how could you construct the correct graph, given only the two original graphs?
You've seen fellow students with rulers different than yours. Which of the rulers you've seen do you think would allow you to construct the most accurate graph?
Using a compass and unmarked straightedge, how could you construct the correct graph?
3. For each of the following make a sketch showing the approximate shape of the graph of y vs. x, showing particularly how the shape of each graph differs from the shapes of the others.
Explanatory note: ^ is the exponentiation operator. For example x^2 means x raised to the power 2, i.e., x * x or x squared. x^3 would be x * x * x, or x cubed.
/ indicates division. 1 / x is 1 divided by x.
If you didn't get these graphs, then make a table showing y vs. x for each one, using x values -2, -1, -1/2, 0, 1/2, 1 and 2. Then sketch your graph based on the table.
4. The trapezoid depicted below can be cut along a single straight line in such a way that the two pieces can be pasted together to form a rectangle. Sketch such a straight line and show how this might be done.
What is the smallest number of cuts required to cut-and-paste the trapezoid below into a rectangle?
A number of students haven't figured this one out yet. Give it another look and see if you can get it.
Some students have shown how to do this in three cuts. At least one has shown how to do it in two cuts, provided certain angles are equal. Is it possible to do this in two cuts with no assumptions on the angles?
5. If you deposit $1000 into an account which every year pays 10% annual interest on the balance at the beginning of that year:
· How much money will you have after each of the first three years?
· At the end of which year do you think your original amount will have doubled?
If you were to graph the amount of money vs. the number of years, would the graph look more like that of x^2, 2^x or 1/x?
6. One car speeds up from 20 mph to 50 mph in 6 seconds. Another speeds up from 120 mph to 140 mph in 5 seconds.
· Which travels further during its given time interval?
· Which is speeding up at the greater rate?
· Which has the greater average speed?
7. Predict the next number in each of the following sequences:
3 4 6 9 13 ...
1 2 4 8 16 ...
50 40 32 26 22 ...
70 38 22 14 10 ...
1 3 4 7 11 18 ...
13 20 39 76 137 ...
Work in some of the notation Michael showed you today.
8. Answer the following:
9. At the beginning of the day there are 400 sane and 600 demented people in a large room. Nobody enters or leaves. Over the course of the day, 10% of the sane people become demented and 20% of the demented people become sane.
How many sane, and how many demented people will there be in the room at the end of the day?
What do you think would happen if the rate at which sane people become demented is 10% * ratio of demented to sane, and the rate at which demented people become sane is 15% * ratio of sane to demented.
The second question is pretty much open-ended.
10. A ball is dropped from a height of 1 meter. It hits the floor and bounces to half of its original height. It then falls back to the floor and bounces to half of that height. The process continues.
How far does the ball travel from the time it is dropped until the time it hits the floor for the third time?
Theoretically, will the ball ever stop?
The time required for a ball to fall to the floor from rest at height y is sqrt( y / 4.9 ), where y is the height in meters. How much time elapses between the first drop and the ball hitting the floor for the third time?
Theoretically, is there a limit to how far the ball can travel?
Theoretically, how far will the ball travel during the infinite length of time required for it to come to rest?
If the ball bounces to 90% of its original height, how far will it travel between drop and third bounce? What is the total distance it will travel, if given an infinite amount of time?
If the ball bounces to r% of its original height, how far will it travel between drop and third bounce? What is the total distance it will travel, if given an infinite amount of time? r stands for an unspecified number between 0 and 100.
11. Report the positions you measured for the ball on the ramp.
If the ramp had been long enough, what do you predict would have been its next three positions?
Obviously the ball was speeding up, getting quicker. Do you think it was getting quicker more and more quickly, less and less quickly, or with about a constant quickiness? How could your data be used to reveal the answer? What are the limitations of your data?