If you square a positive number then take its square root you get the original number. For example, 4^2 = 16, and `sqrt(16) = 4. As long as we are talking about positive numbers we can say that the square root function 'undoes' the squaring function. For that matter, the squaring function also 'undoes' the square root function.

If f(x) = x^2 and g(x) = `sqrt(x), then the process of 'undoing' a function can be expressed as follows:

Start with a number x0.

Apply the function f(x) to x0 to obtain y0 = f(x0).

Apply the function g(x) to y0 to obtain g(y0).

The result is x0.

We see for the present example that y0 = f(x0) = x0 ^ 2.

Then g(y0) = g(x0 ^ 2) = `sqrt(x0 ^ 2).

If x0 is positive, `sqrt(x0 ^ 2) = x0.

When two functions 'undo' one another in the above sense we say that the functions comprise a pair of inverse functions.

1. It was stated above that "As long as we are talking about positive numbers we can say that the square root function 'undoes' the squaring function". Explain why the square root function fails to 'undo' the squaring function if we begin with a negative number (hint: start with a negative number of your choice and show that the square root doesn't undo the square of the number).

2. Give a numerical example of how the squaring function 'undoes' the square root function.

3. Using your calculator, start with any positive number and cube it. Then take the 1/3 power of the result.  This should work whether you start with a positive or a negative number, but some calculators have a little trouble with their arithmetic and give an error when you take the 1/3 power of a negative.  Try it and see.  DERIVE will work in any case.

Do you think that the cubing function and the 1/3 power function comprise a pair of inverse functions?

4. Pick any number x between -3 and 3 and use your calculator to find sin(x). You don't have to know what the sine function is to do this. Just use the sine ('sin') key on your calculator. Then use the inverse sine (you will use the 2d function or the inverse key then the sine key) on this number.

For numbers between -3 and 3, does it seem that the sine function and the inverse sine function make a pair of inverse functions?

5. Let f(x) = e^x and let g(x) = ln(x) (usually the inverse or 2d function of e^x; on some calculators it's the other way around, with the key labeled ln(x) and the 2d function labeled e^x). Pick any positive number for x0 and show that the process described above ('start with x0 ...') ends up returning to x0. Show the same for a negative number of your choice.

Are the functions e^x and ln(x) inverse functions?

Try the same with the 10^x and log(x) functions on your calculator.

The Table

The introduction demonstrated the basic idea of inverse functions. If we understand the tables and graphs of a pair of inverse functions, we will have an even clearer picture.

Here is a table for the function f(x) = x^2, for x = 0 to 5. We call the first column x and the second column u = f(x).

       Squaring Function

x	u = f(x) = x^2
0	0
1	1
2	4
3	9
4	16
5	25

We can form a new table by reversing the columns of this table. We call the first column u to match the label of the column it came from in the first table. We will call the second column w instead of calling it x. This is because x is usually the label for the first column of a table, and w is a convenient enough letter.

Inverse of the Squaring Function

u	w = f^-1(u)
0	0
1	1
4	2
9	3
16	4
25	5

Since we obtained this table by inverting the columns of the first table, we call the second column w the 'inverse' of the function f of the table we inverted. This is why we write w = f^-1(u), which we read as 'w = f inverse of u'.

Now we might well notice that the numbers in the second column of this inverse-function table are just the square roots of the numbers in the first column. So this table is just a partial table for the square root function.

A more detailed table of part of the square root function is shown below:

Detailed Table of Square Root Function

x	u = f(x) = x^.5
0	0
1	1
2	1.41
3	1.72
4	2
5	2.24
6	2.44
7	2.65
8	2.83

We note that the second table, if extended a little more, will contain all the pairs numbers in the 'inverse of the squaring function' table.

Of course the table of the squaring function could have been more extensive. We could have used x values 0, .1, .2, .3, ..., . We could have used x = 0, .01, .02, ..., . We could have made the table as extensive as we might wish. We couldn't really include all the numbers, even between 0 and 5, since there are infinitely many numbers. We can't even devise a scheme for listing all the numbers in order, even if we had an infinite amount of time to complete the listing.

We can, however, imagine that we had some sort of table with all the x values from 0 to 5, and all the squares. This impossible table might look something like this:

 

Impossible Table of f(x) = x^2

x	f(x) = x^2
0	0
All possible values from 0 to 5, in order (not possible)	Corresponding f(x) = x^2 values (must contain all numbers from 0 to 25)
5	25

Of course if we had all possible x values in the first column, we would have all possible numbers from 0 to 25 in the second column. This might seem a bit strange: since the range from 0 to 25 is 5 times the range from 0 to 5, it would seem that some of the numbers in the second column would have to be missing.  However, nothing can be missing, as the following argument shows:

If any number between 0 and 25 was missing from the second column, it would be because its square root was missing from the first. This couldn't be because the first column is supposed to contain all numbers from 0 to 5, and the square root of every number from 0 to 25 must be a number between 0 and 5.  So no number between 0 and 25 is missing from the second column.

The point here is that if we reversed the columns of the 'complete' table of the squaring function, for x from 0 to 5, we would get a complete table of the square root function from 0 to 25.

Inverse Table for f(x) = x^2

u	`sqrt(u)
0	0
All possible values from 0 to 25, in order (not possible)	Corresponding square roots (contains all numbers from 0 to 5)
5	25

Construct a new table by reversing the rows of the original table. Call this table 'inverse of the double of the cube function'.

Now the function z = (.5 u) ^ (1/3) is inverse to the function y = 2 x^3. Show this by picking any number for x. Evaluate y, then plug the result in for u. Show that the z you obtain is the same as the number you started with.

Make a table of z vs. u, using u = 0, 5, 10, 15. Call this table 'z = (.5 u) ^ (1/3).

Sketch a graph of the points on this new table. Sketch a smooth curve through these points.

On the same graph sketch the points corresponding to the 'inverse of the double of the cube function' table.

How does this exercise support the idea that the function obtained by reversing columns is the same as the inverse function that 'undoes' the first function?

7. Construct table for the squaring function f(x) = x^2, using x values between 0 and 2 with a step of .5. Reverse the columns of this table to form a partial table for the inverse function.

Plot the points corresponding to the table of the squaring function, and plot the points corresponding to the table of its inverse. Sketch a smooth curve corresponding to each function.

The diagonal line on the graph is the line y = x. Connect each point on the graph of the squaring function to the corresponding point on the graph of its inverse function. How are these pairs of points positioned with respect to the y = x line?

8. If we reversed the columns of the 'complete' table of the squaring function from 0 to 12, precisely what table would we get?

Sketch the graphs of the functions described by both tables.

9. If we could construct the 'complete' table of the squaring function from 0 to infinity, listing all possible positive numbers in the x column, then why would we be certain that every possible positive number would appear exactly one time in the second column?

What number would appear in the second column next to the number 4.31 in the first column?

What number would appear in the second column next to the number `sqrt(18) in the first column?

What number would appear in the second column next to the number `pi in the first column?

What would we obtain if we reversed the columns of this table?

What number would appear in the second column next to the number 4.31 in the first column of this table?

What number would appear in the second column next to the number `pi^2 in the first column of this table?

What number would appear in the second column next to the number -3 in the first column of this table?

The Graph

If we graph the table shown above for the squaring function we get the following graph:

The points corresponding to the graph of the squaring function f(x) = x^2 are indicated by square marks, while those corresponding to the table of the inverse f(x) = `sqrt(x) of the squaring function are indicated by trianglular marks. The line y = x is provided for reference.

Each point of the squaring function is connected to the corresponding point of the square root function by a line segment that is perpendicular to the line y = x, and this segment is bisected (cut in half) by the y=x line. You will prove that the segment is perpendicular to the y=x line in one of the exercises below. It is also fairly easy to show that the segment is bisector by the line y=x.

The graph below depicts these line segments for several points on the graph.  Note how the (green) segment from point to point is bisected by the y=x line, and how the segment is perpendicular to this line.

The graph below depicts the squaring function f(x) = x^2 and its inverse function g(x) = `sqrt(x). These graphs pass through all the points depicted on the previous graphs, and represent the points on the impossible 'complete' tables of the two functions, with the squaring function including x values from 0 to 5 and its inverse function including x values from 0 to 25.

10. Sketch the graph of the cubing function y = x^3 and of its inverse function y = x^(1/3) for x = -3 to 3. Label pairs of points and connect them with a straight line segment, showing how the segment is bisected by the line y = x and how the points lie at equal distances on either side of the y=x line.

11. When the slopes of two straight lines are negative reciprocals of one another (e.g., 2 and -1/2, 3/4 and -4/3, m and -1/m) the lines are perpendicular.

Use this fact to prove that the line segment between the point (2,4) on the graph of the squaring function and the point (4,2) on the graph of its inverse function is perpendicular to the line y = x.  (Hint:  get the equation for the line from (2,4) to (4,2) and check out its slope).

Prove that for any number a the line segment between (a, a^2) and (a^2, a) is perpendicular to the line y = x.

Preliminary Exercise: Make a table of the function y = 2^x for x = -3 to 3, with step 1. Make the corresponding partial table for the inverse function. Plot both functions on the same graph and repeat problem #10 for this graph. The inverse function is the base-2 logarithm function, denoted y = log{base2} (x).

A table of the function y = 2^x is depicted below:

Table of y = 2^x

x	y = 2^x
-3	.125
-2	.25
-1	.5
0	1
1	2
2	4
3	8
4	16

The corresponding table of its inverse function is:

Table of Inverse of y = 2^x function

x	inverse function of y = 2^x y = log{base 2} (x)
8	3
4	2
2	1
1	0
.5	-1
.25	-2
.125	-3

The graph of the table points for both y = 2^x and y = log{base 2} (x)  is shown below.

The continuous graph of the y = 2^x function and its inverse function y = log{base 2} (x) is as shown on the two graphs below. The graphs are identical except that the second graph has approximately equal scales on the x and y axes, so that the y = x line can be visualized at a 45 degree angle, with the segment between corresponding points bisected by this line at a right angle. The first graph, with unequal scales, is of a more convenient shape, though it distorts angles.

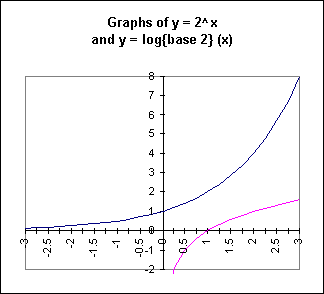
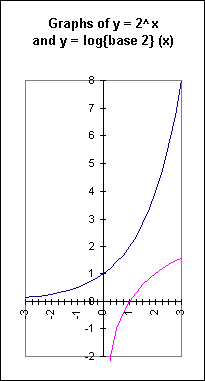
Translating 2^x = y into logarithmic form

It should be clear that if (x,y) is a point on the graph of the exponential function, the point (y,x) lies on the graph of the logarithmic function, and vice versa.  This leads us to the following pairs of equivalent statements:

{1A:  (x,y) lies on the graph of the exponential function} equivalent to    {1B:  y = 2^x}.

{2A:  (y,x) lies on the graph of the logarithmic function} equivalent to     {2B:  (x,y) lies on the graph the exponential function}.

{3A:  (y,x) lies on the graph of the logarithmic function} equivalent to     {3B:  x = log{base 2} (y)}.

Since statements 1A and 2B are equivalent we easily conclude that all statements in the first and second pair are equivalent.

Since statements 2A and 3A are equivalent we similarly conclude that all statements in the second and second third are equivalent.

So we conclude that every one of the statements is equivalent to any other

In particular . 1B and 3B are equivalent, so y = 2^x is equivalent to x = log{base 2} (y).

y = 2^x can be translated to x = log{base 2} (y).

This statement permits us to translate an equation with x in the exponent, where we can find its value only by approximation, to an equation where x is no longer in the exponent. We can find x if we can evaluate the base-2 logarithm of y, which turns out to be very easy if we know the value of y.

We will see later that

log{base 2} (y) = log(y) / log(2).  

We can evaluate log(2) or log(y) with our calculator, provided we know the value of y.

Solving an equation of form y = 2^x for x

This provides us with a means of solving an equation like 2 ^ x = 16. Of course we know that 16 is the fourth power of 2, so the solution of the equation is x = 4. However it is instructive to solve this equation using the above ideas, as follows:

2^x = 16 is first translated into the form x = log{base 2} (16).

The expression log{base 2} (16) is translated into the expression log(16) / log(2).

This expression is evaluated using a calculator. We obtain

x = log(16) / log(2) = 1.204 / .301 = 4.

This solution method works, of course, for an equation like 2 ^ x = 11, where the right-hand side is not an integer power of x. For this equation we would proceed as follows:

2^x = 11 is first translated into the form x = log{base 2} (16).

The expression log{base 2} (11) is translated intoto the expression log(11) / log(2).

This expression is evaluated using a calculator.

We obtain x = log(11) / log(2) = 1.041 / .301 = 3.46.

12. Construct a table for the function y = 2^x, from x = -5 to 5. Construct the corresponding table for y = log{base 2} (x). Sketch the points corresponding to both tables on the graph below.

Use your graph to estimate the base-2 logarithms of 3, 10 and 25. Check your estimates against the results given by your calculator, recalling that for example log {base 2} (3) = log 3 / log 2.

13. Translate each of the following exponential equations into equations involving logarithms, and solve where possible: