2.1 Displacement
Figure 2.59
1.
Find the following for path A in Figure 2.59: (a) The distance traveled.(b) The magnitude of the displacement from start to finish. (c) The
displacement from start to finish.
2.
Find the following for path B in Figure 2.59: (a) The distance traveled.(b) The magnitude of the displacement from start to finish. (c) The
displacement from start to finish.
3.
Find the following for path C in Figure 2.59: (a) The distance traveled.(b) The magnitude of the displacement from start to finish. (c) The
displacement from start to finish.
4.
Find the following for path D in Figure 2.59: (a) The distance traveled.(b) The magnitude of the displacement from start to finish. (c) The
displacement from start to finish.
2.3 Time, Velocity, and Speed
5.
(a) Calculate Earth’s average speed relative to the Sun. (b) What is itsaverage velocity over a period of one year?
6.
A helicopter blade spins at exactly 100 revolutions per minute. Its tip is5.00 m from the center of rotation. (a) Calculate the average speed of the
blade tip in the helicopter’s frame of reference. (b) What is its average
velocity over one revolution?
7.
The North American and European continents are moving apart at arate of about 3 cm/y. At this rate how long will it take them to drift 500 km
farther apart than they are at present?
8.
Land west of the San Andreas fault in southern California is moving atan average velocity of about 6 cm/y northwest relative to land east of the
fault. Los Angeles is west of the fault and may thus someday be at the
same latitude as San Francisco, which is east of the fault. How far in the
future will this occur if the displacement to be made is 590 km northwest,
assuming the motion remains constant?
9.
On May 26, 1934, a streamlined, stainless steel diesel train called theZephyr set the world’s nonstop long-distance speed record for trains. Its
run from Denver to Chicago took 13 hours, 4 minutes, 58 seconds, and
was witnessed by more than a million people along the route. The total
distance traveled was 1633.8 km. What was its average speed in km/h
and m/s?
10.
Tidal friction is slowing the rotation of the Earth. As a result, the orbitof the Moon is increasing in radius at a rate of approximately 4 cm/year.
Assuming this to be a constant rate, how many years will pass before the
radius of the Moon’s orbit increases by
3.84×106 m (1%)?11.
A student drove to the university from her home and noted that theodometer reading of her car increased by 12.0 km. The trip took 18.0
min. (a) What was her average speed? (b) If the straight-line distance
from her home to the university is 10.3 km in a direction
25.0º south ofeast, what was her average velocity? (c) If she returned home by the
same path 7 h 30 min after she left, what were her average speed and
velocity for the entire trip?
12.
The speed of propagation of the action potential (an electrical signal)in a nerve cell depends (inversely) on the diameter of the axon (nerve
fiber). If the nerve cell connecting the spinal cord to your feet is 1.1 m
long, and the nerve impulse speed is 18 m/s, how long does it take for
the nerve signal to travel this distance?
13.
Conversations with astronauts on the lunar surface werecharacterized by a kind of echo in which the earthbound person’s voice
was so loud in the astronaut’s space helmet that it was picked up by the
astronaut’s microphone and transmitted back to Earth. It is reasonable to
assume that the echo time equals the time necessary for the radio wave
to travel from the Earth to the Moon and back (that is, neglecting any time
delays in the electronic equipment). Calculate the distance from Earth to
the Moon given that the echo time was 2.56 s and that radio waves travel
at the speed of light
(3.00×108 m/s) .14.
A football quarterback runs 15.0 m straight down the playing field in2.50 s. He is then hit and pushed 3.00 m straight backward in 1.75 s. He
breaks the tackle and runs straight forward another 21.0 m in 5.20 s.
Calculate his average velocity (a) for each of the three intervals and (b)
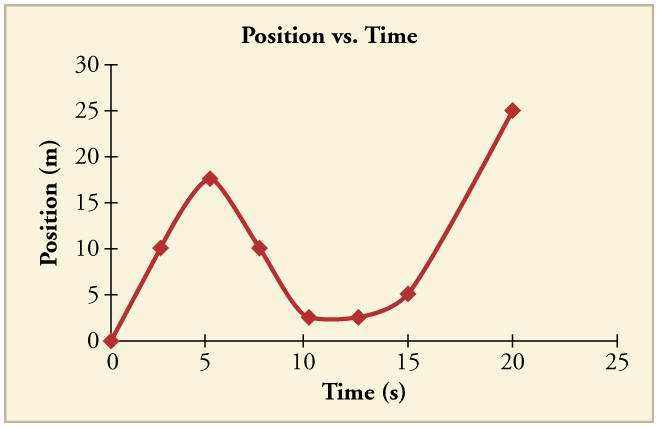
for the entire motion.
15.
The planetary model of the atom pictures electrons orbiting theatomic nucleus much as planets orbit the Sun. In this model you can view
hydrogen, the simplest atom, as having a single electron in a circular
orbit
1.06×10−10 m in diameter. (a) If the average speed of theelectron in this orbit is known to be
2.20×106 m/s , calculate thenumber of revolutions per second it makes about the nucleus. (b) What is
the electron’s average velocity?
2.4 Acceleration
16.
A cheetah can accelerate from rest to a speed of 30.0 m/s in 7.00 s.What is its acceleration?
17. Professional Application
Dr. John Paul Stapp was U.S. Air Force officer who studied the effects of
extreme deceleration on the human body. On December 10, 1954, Stapp
rode a rocket sled, accelerating from rest to a top speed of 282 m/s (1015
km/h) in 5.00 s, and was brought jarringly back to rest in only 1.40 s!
Calculate his (a) acceleration and (b) deceleration. Express each in
multiples of
g (9.80 m/s2) by taking its ratio to the acceleration ofgravity.
18.
A commuter backs her car out of her garage with an acceleration of1.40 m/s
2 . (a) How long does it take her to reach a speed of 2.00 m/s?(b) If she then brakes to a stop in 0.800 s, what is her deceleration?
19.
Assume that an intercontinental ballistic missile goes from rest to asuborbital speed of 6.50 km/s in 60.0 s (the actual speed and time are
classified). What is its average acceleration in
m/s2 and in multiples ofg
(9.80 m/s2)?2.5 Motion Equations for Constant Acceleration in One
Dimension
20.
An Olympic-class sprinter starts a race with an acceleration of4.50 m/s
2 . (a) What is her speed 2.40 s later? (b) Sketch a graph of herposition vs. time for this period.
21.
A well-thrown ball is caught in a well-padded mitt. If the decelerationof the ball is
2.10×104 m/s2 , and 1.85 ms (1 ms = 10−3 s) elapsesfrom the time the ball first touches the mitt until it stops, what was the
initial velocity of the ball?
22.
A bullet in a gun is accelerated from the firing chamber to the end ofthe barrel at an average rate of
6.20×105 m/s2 for 8.10×10−4 s .What is its muzzle velocity (that is, its final velocity)?
23.
(a) A light-rail commuter train accelerates at a rate of 1.35 m/s2 .How long does it take to reach its top speed of 80.0 km/h, starting from
CHAPTER 2 | KINEMATICS 81
rest? (b) The same train ordinarily decelerates at a rate of
1.65 m/s2 .How long does it take to come to a stop from its top speed? (c) In
emergencies the train can decelerate more rapidly, coming to rest from
80.0 km/h in 8.30 s. What is its emergency deceleration in
m/s2 ?24.
While entering a freeway, a car accelerates from rest at a rate of2.40 m/s
2 for 12.0 s. (a) Draw a sketch of the situation. (b) List theknowns in this problem. (c) How far does the car travel in those 12.0 s?
To solve this part, first identify the unknown, and then discuss how you
chose the appropriate equation to solve for it. After choosing the
equation, show your steps in solving for the unknown, check your units,
and discuss whether the answer is reasonable. (d) What is the car’s final
velocity? Solve for this unknown in the same manner as in part (c),
showing all steps explicitly.
25.
At the end of a race, a runner decelerates from a velocity of 9.00 m/sat a rate of
2.00 m/s2 . (a) How far does she travel in the next 5.00 s?(b) What is her final velocity? (c) Evaluate the result. Does it make
sense?
26. Professional Application:
Blood is accelerated from rest to 30.0 cm/s in a distance of 1.80 cm by
the left ventricle of the heart. (a) Make a sketch of the situation. (b) List
the knowns in this problem. (c) How long does the acceleration take? To
solve this part, first identify the unknown, and then discuss how you
chose the appropriate equation to solve for it. After choosing the
equation, show your steps in solving for the unknown, checking your
units. (d) Is the answer reasonable when compared with the time for a
heartbeat?
27.
In a slap shot, a hockey player accelerates the puck from a velocity of8.00 m/s to 40.0 m/s in the same direction. If this shot takes
3.33×10
−2 s , calculate the distance over which the puck accelerates.28.
A powerful motorcycle can accelerate from rest to 26.8 m/s (100 km/h) in only 3.90 s. (a) What is its average acceleration? (b) How far does it
travel in that time?
29.
Freight trains can produce only relatively small accelerations anddecelerations. (a) What is the final velocity of a freight train that
accelerates at a rate of
0.0500 m/s2 for 8.00 min, starting with an initialvelocity of 4.00 m/s? (b) If the train can slow down at a rate of
0.550 m/s
2 , how long will it take to come to a stop from this velocity?(c) How far will it travel in each case?
30.
A fireworks shell is accelerated from rest to a velocity of 65.0 m/sover a distance of 0.250 m. (a) How long did the acceleration last? (b)
Calculate the acceleration.
31.
A swan on a lake gets airborne by flapping its wings and running ontop of the water. (a) If the swan must reach a velocity of 6.00 m/s to take
off and it accelerates from rest at an average rate of
0.350 m/s2 , howfar will it travel before becoming airborne? (b) How long does this take?
32. Professional Application:
A woodpecker’s brain is specially protected from large decelerations by
tendon-like attachments inside the skull. While pecking on a tree, the
woodpecker’s head comes to a stop from an initial velocity of 0.600 m/s
in a distance of only 2.00 mm. (a) Find the acceleration in
m/s2 and inmultiples of
g⎛⎝g
= 9.80 m/s2⎞⎠. (b) Calculate the stopping time. (c) The
tendons cradling the brain stretch, making its stopping distance 4.50 mm
(greater than the head and, hence, less deceleration of the brain). What
is the brain’s deceleration, expressed in multiples of
g ?33.
An unwary football player collides with a padded goalpost whilerunning at a velocity of 7.50 m/s and comes to a full stop after
compressing the padding and his body 0.350 m. (a) What is his
deceleration? (b) How long does the collision last?
34.
In World War II, there were several reported cases of airmen whojumped from their flaming airplanes with no parachute to escape certain
death. Some fell about 20,000 feet (6000 m), and some of them survived,
with few life-threatening injuries. For these lucky pilots, the tree branches
and snow drifts on the ground allowed their deceleration to be relatively
small. If we assume that a pilot’s speed upon impact was 123 mph (54
m/s), then what was his deceleration? Assume that the trees and snow
stopped him over a distance of 3.0 m.
35.
Consider a grey squirrel falling out of a tree to the ground. (a) If weignore air resistance in this case (only for the sake of this problem),
determine a squirrel’s velocity just before hitting the ground, assuming it
fell from a height of 3.0 m. (b) If the squirrel stops in a distance of 2.0 cm
through bending its limbs, compare its deceleration with that of the
airman in the previous problem.
36.
An express train passes through a station. It enters with an initialvelocity of 22.0 m/s and decelerates at a rate of
0.150 m/s2 as it goesthrough. The station is 210 m long. (a) How long is the nose of the train in
the station? (b) How fast is it going when the nose leaves the station? (c)
If the train is 130 m long, when does the end of the train leave the
station? (d) What is the velocity of the end of the train as it leaves?
37.
Dragsters can actually reach a top speed of 145 m/s in only 4.45s—considerably less time than given in
Example 2.10 and Example2.11
. (a) Calculate the average acceleration for such a dragster. (b) Findthe final velocity of this dragster starting from rest and accelerating at the
rate found in (a) for 402 m (a quarter mile) without using any information
on time. (c) Why is the final velocity greater than that used to find the
average acceleration?
Hint: Consider whether the assumption of constantacceleration is valid for a dragster. If not, discuss whether the
acceleration would be greater at the beginning or end of the run and what
effect that would have on the final velocity.
38.
A bicycle racer sprints at the end of a race to clinch a victory. Theracer has an initial velocity of 11.5 m/s and accelerates at the rate of
0.500 m/s
2 for 7.00 s. (a) What is his final velocity? (b) The racercontinues at this velocity to the finish line. If he was 300 m from the finish
line when he started to accelerate, how much time did he save? (c) One
other racer was 5.00 m ahead when the winner started to accelerate, but
he was unable to accelerate, and traveled at 11.8 m/s until the finish line.
How far ahead of him (in meters and in seconds) did the winner finish?
39.
In 1967, New Zealander Burt Munro set the world record for an Indianmotorcycle, on the Bonneville Salt Flats in Utah, of 183.58 mi/h. The oneway
course was 5.00 mi long. Acceleration rates are often described by
the time it takes to reach 60.0 mi/h from rest. If this time was 4.00 s, and
Burt accelerated at this rate until he reached his maximum speed, how
long did it take Burt to complete the course?
40.
(a) A world record was set for the men’s 100-m dash in the 2008Olympic Games in Beijing by Usain Bolt of Jamaica. Bolt “coasted”
across the finish line with a time of 9.69 s. If we assume that Bolt
accelerated for 3.00 s to reach his maximum speed, and maintained that
speed for the rest of the race, calculate his maximum speed and his
acceleration. (b) During the same Olympics, Bolt also set the world
record in the 200-m dash with a time of 19.30 s. Using the same
assumptions as for the 100-m dash, what was his maximum speed for
this race?
2.7 Falling Objects
41.
Assume air resistance is negligible unless otherwise stated.42.
Calculate the displacement and velocity at times of (a) 0.500, (b)1.00, (c) 1.50, and (d) 2.00 s for a ball thrown straight up with an initial
velocity of 15.0 m/s. Take the point of release to be
y0 = 0 .43.
Calculate the displacement and velocity at times of (a) 0.500, (b)1.00, (c) 1.50, (d) 2.00, and (e) 2.50 s for a rock thrown straight down
with an initial velocity of 14.0 m/s from the Verrazano Narrows Bridge in
New York City. The roadway of this bridge is 70.0 m above the water.
44.
A basketball referee tosses the ball straight up for the starting tip-off.At what velocity must a basketball player leave the ground to rise 1.25 m
above the floor in an attempt to get the ball?
45.
A rescue helicopter is hovering over a person whose boat has sunk.One of the rescuers throws a life preserver straight down to the victim
with an initial velocity of 1.40 m/s and observes that it takes 1.8 s to
82 CHAPTER 2 | KINEMATICS
reach the water. (a) List the knowns in this problem. (b) How high above
the water was the preserver released? Note that the downdraft of the
helicopter reduces the effects of air resistance on the falling life
preserver, so that an acceleration equal to that of gravity is reasonable.
46.
A dolphin in an aquatic show jumps straight up out of the water at avelocity of 13.0 m/s. (a) List the knowns in this problem. (b) How high
does his body rise above the water? To solve this part, first note that the
final velocity is now a known and identify its value. Then identify the
unknown, and discuss how you chose the appropriate equation to solve
for it. After choosing the equation, show your steps in solving for the
unknown, checking units, and discuss whether the answer is reasonable.
(c) How long is the dolphin in the air? Neglect any effects due to his size
or orientation.
47.
A swimmer bounces straight up from a diving board and falls feet firstinto a pool. She starts with a velocity of 4.00 m/s, and her takeoff point is
1.80 m above the pool. (a) How long are her feet in the air? (b) What is
her highest point above the board? (c) What is her velocity when her feet
hit the water?
48.
(a) Calculate the height of a cliff if it takes 2.35 s for a rock to hit theground when it is thrown straight up from the cliff with an initial velocity of
8.00 m/s. (b) How long would it take to reach the ground if it is thrown
straight down with the same speed?
49.
A very strong, but inept, shot putter puts the shot straight up verticallywith an initial velocity of 11.0 m/s. How long does he have to get out of
the way if the shot was released at a height of 2.20 m, and he is 1.80 m
tall?
50.
You throw a ball straight up with an initial velocity of 15.0 m/s. Itpasses a tree branch on the way up at a height of 7.00 m. How much
additional time will pass before the ball passes the tree branch on the
way back down?
51.
A kangaroo can jump over an object 2.50 m high. (a) Calculate itsvertical speed when it leaves the ground. (b) How long is it in the air?
52.
Standing at the base of one of the cliffs of Mt. Arapiles in Victoria,Australia, a hiker hears a rock break loose from a height of 105 m. He
can’t see the rock right away but then does, 1.50 s later. (a) How far
above the hiker is the rock when he can see it? (b) How much time does
he have to move before the rock hits his head?
53.
An object is dropped from a height of 75.0 m above ground level. (a)Determine the distance traveled during the first second. (b) Determine
the final velocity at which the object hits the ground. (c) Determine the
distance traveled during the last second of motion before hitting the
ground.
54.
There is a 250-m-high cliff at Half Dome in Yosemite National Park inCalifornia. Suppose a boulder breaks loose from the top of this cliff. (a)
How fast will it be going when it strikes the ground? (b) Assuming a
reaction time of 0.300 s, how long will a tourist at the bottom have to get
out of the way after hearing the sound of the rock breaking loose
(neglecting the height of the tourist, which would become negligible
anyway if hit)? The speed of sound is 335 m/s on this day.
55.
A ball is thrown straight up. It passes a 2.00-m-high window 7.50 moff the ground on its path up and takes 1.30 s to go past the window.
What was the ball’s initial velocity?
56.
Suppose you drop a rock into a dark well and, using precisionequipment, you measure the time for the sound of a splash to return. (a)
Neglecting the time required for sound to travel up the well, calculate the
distance to the water if the sound returns in 2.0000 s. (b) Now calculate
the distance taking into account the time for sound to travel up the well.
The speed of sound is 332.00 m/s in this well.
57.
A steel ball is dropped onto a hard floor from a height of 1.50 m andrebounds to a height of 1.45 m. (a) Calculate its velocity just before it
strikes the floor. (b) Calculate its velocity just after it leaves the floor on its
way back up. (c) Calculate its acceleration during contact with the floor if
that contact lasts 0.0800 ms
(8.00×10−5 s) . (d) How much did the ballcompress during its collision with the floor, assuming the floor is
absolutely rigid?
58.
A coin is dropped from a hot-air balloon that is 300 m above theground and rising at 10.0 m/s upward. For the coin, find (a) the maximum
height reached, (b) its position and velocity 4.00 s after being released,
and (c) the time before it hits the ground.
59.
A soft tennis ball is dropped onto a hard floor from a height of 1.50 mand rebounds to a height of 1.10 m. (a) Calculate its velocity just before it
strikes the floor. (b) Calculate its velocity just after it leaves the floor on its
way back up. (c) Calculate its acceleration during contact with the floor if
that contact lasts 3.50 ms
(3.50×10−3 s) . (d) How much did the ballcompress during its collision with the floor, assuming the floor is
absolutely rigid?
2.8 Graphical Analysis of One-Dimensional Motion
Note: There is always uncertainty in numbers taken from graphs. If your
answers differ from expected values, examine them to see if they are
within data extraction uncertainties estimated by you.
60.
(a) By taking the slope of the curve in Figure 2.60, verify that thevelocity of the jet car is 115 m/s at
t = 20 s . (b) By taking the slope ofthe curve at any point in
Figure 2.61, verify that the jet car’s accelerationis
5.0 m/s2 .Figure 2.60
Figure 2.61
61.
Take the slope of the curve in Figure 2.62 to verify that the velocity att
= 10 s is 207 m/s.Figure 2.62
62.
Take the slope of the curve in Figure 2.62 to verify that the velocity att
= 30.0 s is 238 m/s.63.
By taking the slope of the curve in Figure 2.63, verify that theacceleration is
3.2 m/s2 at t = 10 s .CHAPTER 2 | KINEMATICS 83
Figure 2.63
64.
Construct the displacement graph for the subway shuttle train asshown in
Figure 2.48(a). You will need to use the information onacceleration and velocity given in the examples for this figure.
65.
(a) Take the slope of the curve in Figure 2.64 to find the jogger’svelocity at
t = 2.5 s . (b) Repeat at 7.5 s. These values must beconsistent with the graph in
Figure 2.65.Figure 2.64
Figure 2.65

Figure 2.66
66.
A graph of v(t) is shown for a world-class track sprinter in a 100-mrace. (See
Figure 2.67). (a) What is his average velocity for the first 4 s?(b) What is his instantaneous velocity at
t = 5 s ? (c) What is hisaverage acceleration between 0 and 4 s? (d) What is his time for the
race?
Figure 2.67
67.
Figure 2.68 shows the displacement graph for a particle for 5 s. Drawthe corresponding velocity and acceleration graphs.
Figure 2.68
84 CHAPTER 2 | KINEMATICS
answers.
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 117
Problems & Exercises
3.2 Vector Addition and Subtraction: Graphical Methods
Use graphical methods to solve these problems. You may assume
data taken from graphs is accurate to three digits.
1.
Find the following for path A in Figure 3.54: (a) the total distancetraveled, and (b) the magnitude and direction of the displacement from
start to finish.
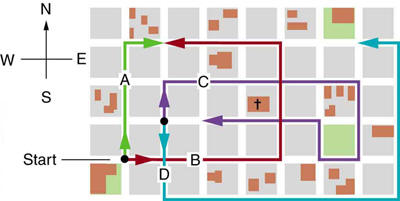
Figure 3.54
The various lines represent paths taken by different people walking in acity. All blocks are 120 m on a side.
2.
Find the following for path B in Figure 3.54: (a) the total distancetraveled, and (b) the magnitude and direction of the displacement from
start to finish.
3.
Find the north and east components of the displacement for the hikersshown in
Figure 3.52.4.
Suppose you walk 18.0 m straight west and then 25.0 m straight north.How far are you from your starting point, and what is the compass
direction of a line connecting your starting point to your final position? (If
you represent the two legs of the walk as vector displacements
A andB
, as in Figure 3.55, then this problem asks you to find their sumR
= A + B .)
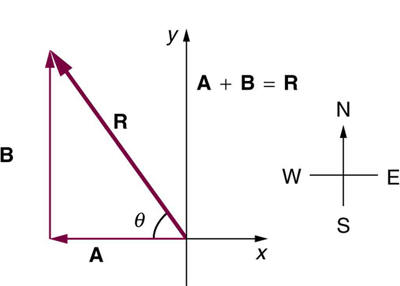
Figure 3.55
The two displacements A and B add to give a total displacement Rhaving magnitude
R and direction θ .5.
Suppose you first walk 12.0 m in a direction 20º west of north andthen 20.0 m in a direction
40.0º south of west. How far are you fromyour starting point, and what is the compass direction of a line connecting
your starting point to your final position? (If you represent the two legs of
the walk as vector displacements
A and B , as in Figure 3.56, then thisproblem finds their sum
R = A + B .)
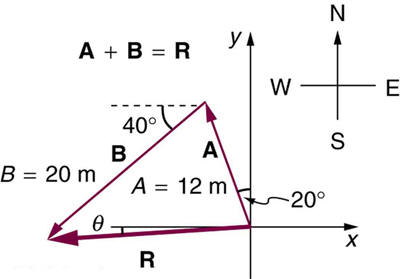
Figure 3.56
6.
Repeat the problem above, but reverse the order of the two legs of thewalk; show that you get the same final result. That is, you first walk leg
B
, which is 20.0 m in a direction exactly 40º south of west, and thenleg
A , which is 12.0 m in a direction exactly 20º west of north. (Thisproblem shows that
A + B = B + A .)7.
(a) Repeat the problem two problems prior, but for the second leg youwalk 20.0 m in a direction
40.0º north of east (which is equivalent tosubtracting
B from A —that is, to finding R′ = A − B ). (b) Repeatthe problem two problems prior, but now you first walk 20.0 m in a
direction
40.0º south of west and then 12.0 m in a direction 20.0º eastof south (which is equivalent to subtracting
A from B —that is, tofinding
R′′ = B - A = - R′ ). Show that this is the case.8.
Show that the order of addition of three vectors does not affect theirsum. Show this property by choosing any three vectors
A , B , and C ,all having different lengths and directions. Find the sum
A + B + Cthen find their sum when added in a different order and show the result is
the same. (There are five other orders in which
A , B , and C can beadded; choose only one.)
9.
Show that the sum of the vectors discussed in Example 3.2 gives theresult shown in
Figure 3.24.10.
Find the magnitudes of velocities vA and vB in Figure 3.57
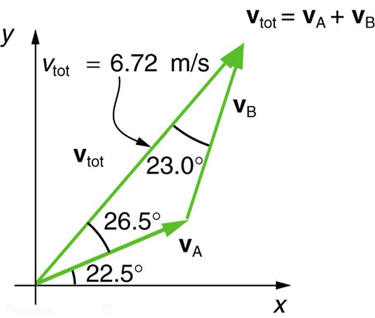
Figure 3.57
The two velocities vA and vB add to give a total vtot .11.
Find the components of vtot along the x- and y-axes in Figure 3.57.12.
Find the components of vtot along a set of perpendicular axesrotated
30º counterclockwise relative to those in Figure 3.57.3.3 Vector Addition and Subtraction: Analytical Methods
13.
Find the following for path C in Figure 3.58: (a) the total distancetraveled and (b) the magnitude and direction of the displacement from
start to finish. In this part of the problem, explicitly show how you follow
the steps of the analytical method of vector addition.
118 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS

Figure 3.58
The various lines represent paths taken by different people walking in acity. All blocks are 120 m on a side.
14.
Find the following for path D in Figure 3.58: (a) the total distancetraveled and (b) the magnitude and direction of the displacement from
start to finish. In this part of the problem, explicitly show how you follow
the steps of the analytical method of vector addition.
15.
Find the north and east components of the displacement from SanFrancisco to Sacramento shown in
Figure 3.59.
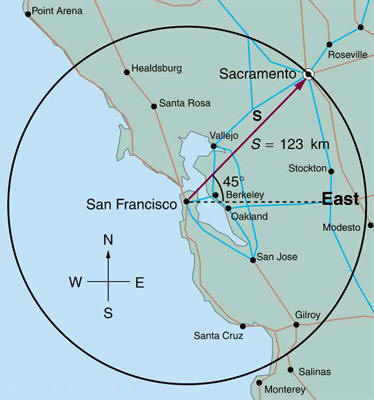
Figure 3.59
16.
Solve the following problem using analytical techniques: Suppose youwalk 18.0 m straight west and then 25.0 m straight north. How far are you
from your starting point, and what is the compass direction of a line
connecting your starting point to your final position? (If you represent the
two legs of the walk as vector displacements
A and B , as in Figure3.60
, then this problem asks you to find their sum R = A + B .)

Figure 3.60
The two displacements A and B add to give a total displacement Rhaving magnitude
R and direction θ .Note that you can also solve this graphically. Discuss why the analytical
technique for solving this problem is potentially more accurate than the
graphical technique.
17.
Repeat Exercise 3.16 using analytical techniques, but reverse theorder of the two legs of the walk and show that you get the same final
result. (This problem shows that adding them in reverse order gives the
same result—that is,
B + A = A + B .) Discuss how taking anotherpath to reach the same point might help to overcome an obstacle
blocking you other path.
18.
You drive 7.50 km in a straight line in a direction 15º east of north.(a) Find the distances you would have to drive straight east and then
straight north to arrive at the same point. (This determination is
equivalent to find the components of the displacement along the east and
north directions.) (b) Show that you still arrive at the same point if the
east and north legs are reversed in order.
19.
Do Exercise 3.16 again using analytical techniques and change thesecond leg of the walk to
25.0 m straight south. (This is equivalent tosubtracting
B from A —that is, finding R′ = A – B ) (b) Repeatagain, but now you first walk
25.0 m north and then 18.0 m east. (Thisis equivalent to subtract
A from B —that is, to find A = B + C . Isthat consistent with your result?)
20.
A new landowner has a triangular piece of flat land she wishes tofence. Starting at the west corner, she measures the first side to be 80.0
m long and the next to be 105 m. These sides are represented as
displacement vectors
A from B in Figure 3.61. She then correctlycalculates the length and orientation of the third side
C . What is herresult?
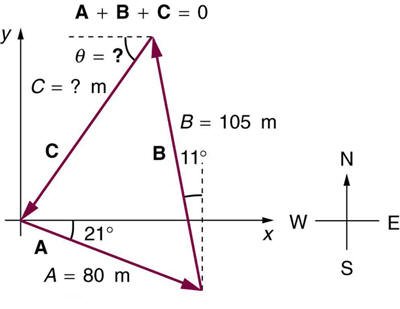
Figure 3.61
21.
You fly 32.0 km in a straight line in still air in the direction 35.0ºsouth of west. (a) Find the distances you would have to fly straight south
and then straight west to arrive at the same point. (This determination is
equivalent to finding the components of the displacement along the south
and west directions.) (b) Find the distances you would have to fly first in a
direction
45.0º south of west and then in a direction 45.0º west ofnorth. These are the components of the displacement along a different
set of axes—one rotated
45º .22.
A farmer wants to fence off his four-sided plot of flat land. Hemeasures the first three sides, shown as
A, B, and C in Figure 3.62,and then correctly calculates the length and orientation of the fourth side
D
. What is his result?
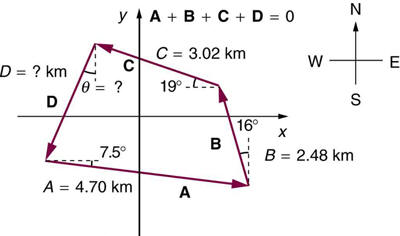
Figure 3.62
23.
In an attempt to escape his island, Gilligan builds a raft and sets tosea. The wind shifts a great deal during the day, and he is blown along
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 119
the following straight lines:
2.50 km 45.0º north of west; then4.70 km 60.0º
south of east; then 1.30 km 25.0º south of west;then
5.10 km straight east; then 1.70 km 5.00º east of north; then7.20 km 55.0º
south of west; and finally 2.80 km 10.0º north ofeast. What is his final position relative to the island?
24.
Suppose a pilot flies 40.0 km in a direction 60º north of east andthen flies
30.0 km in a direction 15º north of east as shown in Figure3.63
. Find her total distance R from the starting point and the directionθ
of the straight-line path to the final position. Discuss qualitatively howthis flight would be altered by a wind from the north and how the effect of
the wind would depend on both wind speed and the speed of the plane
relative to the air mass.
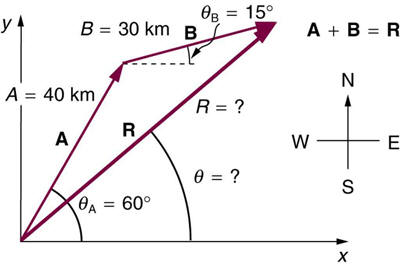
Figure 3.63
3.4 Projectile Motion
25.
A projectile is launched at ground level with an initial speed of 50.0m/s at an angle of
30.0º above the horizontal. It strikes a target abovethe ground 3.00 seconds later. What are the
x and y distances fromwhere the projectile was launched to where it lands?
26.
A ball is kicked with an initial velocity of 16 m/s in the horizontaldirection and 12 m/s in the vertical direction. (a) At what speed does the
ball hit the ground? (b) For how long does the ball remain in the air?
(c)What maximum height is attained by the ball?
27.
A ball is thrown horizontally from the top of a 60.0-m building andlands 100.0 m from the base of the building. Ignore air resistance. (a)
How long is the ball in the air? (b) What must have been the initial
horizontal component of the velocity? (c) What is the vertical component
of the velocity just before the ball hits the ground? (d) What is the velocity
(including both the horizontal and vertical components) of the ball just
before it hits the ground?
28.
(a) A daredevil is attempting to jump his motorcycle over a line ofbuses parked end to end by driving up a
32º ramp at a speed of40.0 m/s (144 km/h)
. How many buses can he clear if the top of thetakeoff ramp is at the same height as the bus tops and the buses are
20.0 m long? (b) Discuss what your answer implies about the margin of
error in this act—that is, consider how much greater the range is than the
horizontal distance he must travel to miss the end of the last bus.
(Neglect air resistance.)
29.
An archer shoots an arrow at a 75.0 m distant target; the bull’s-eye ofthe target is at same height as the release height of the arrow. (a) At what
angle must the arrow be released to hit the bull’s-eye if its initial speed is
35.0 m/s? In this part of the problem, explicitly show how you follow the
steps involved in solving projectile motion problems. (b) There is a large
tree halfway between the archer and the target with an overhanging
horizontal branch 3.50 m above the release height of the arrow. Will the
arrow go over or under the branch?
30.
A rugby player passes the ball 7.00 m across the field, where it iscaught at the same height as it left his hand. (a) At what angle was the
ball thrown if its initial speed was 12.0 m/s, assuming that the smaller of
the two possible angles was used? (b) What other angle gives the same
range, and why would it not be used? (c) How long did this pass take?
31.
Verify the ranges for the projectiles in Figure 3.41(a) for θ = 45ºand the given initial velocities.
32.
Verify the ranges shown for the projectiles in Figure 3.41(b) for aninitial velocity of 50 m/s at the given initial angles.
33.
The cannon on a battleship can fire a shell a maximum distance of32.0 km. (a) Calculate the initial velocity of the shell. (b) What maximum
height does it reach? (At its highest, the shell is above 60% of the
atmosphere—but air resistance is not really negligible as assumed to
make this problem easier.) (c) The ocean is not flat, because the Earth is
curved. Assume that the radius of the Earth is
6.37×103 km . Howmany meters lower will its surface be 32.0 km from the ship along a
horizontal line parallel to the surface at the ship? Does your answer imply
that error introduced by the assumption of a flat Earth in projectile motion
is significant here?
34.
An arrow is shot from a height of 1.5 m toward a cliff of height H . Itis shot with a velocity of 30 m/s at an angle of
60º above the horizontal.It lands on the top edge of the cliff 4.0 s later. (a) What is the height of the
cliff? (b) What is the maximum height reached by the arrow along its
trajectory? (c) What is the arrow’s impact speed just before hitting the
cliff?
35.
In the standing broad jump, one squats and then pushes off with thelegs to see how far one can jump. Suppose the extension of the legs
from the crouch position is 0.600 m and the acceleration achieved from
this position is 1.25 times the acceleration due to gravity,
g . How far canthey jump? State your assumptions. (Increased range can be achieved
by swinging the arms in the direction of the jump.)
36.
The world long jump record is 8.95 m (Mike Powell, USA, 1991).Treated as a projectile, what is the maximum range obtainable by a
person if he has a take-off speed of 9.5 m/s? State your assumptions.
37.
Serving at a speed of 170 km/h, a tennis player hits the ball at aheight of 2.5 m and an angle
θ below the horizontal. The service line is11.9 m from the net, which is 0.91 m high. What is the angle
θ such thatthe ball just crosses the net? Will the ball land in the service box, whose
out line is 6.40 m from the net?
38.
A football quarterback is moving straight backward at a speed of 200m/s when he throws a pass to a player 18.0 m straight downfield. (a) If
the ball is thrown at an angle of
25º relative to the ground and is caughtat the same height as it is released, what is its initial speed relative to the
ground? (b) How long does it take to get to the receiver? (c) What is its
maximum height above its point of release?
39.
Gun sights are adjusted to aim high to compensate for the effect ofgravity, effectively making the gun accurate only for a specific range. (a) If
a gun is sighted to hit targets that are at the same height as the gun and
100.0 m away, how low will the bullet hit if aimed directly at a target 150.0
m away? The muzzle velocity of the bullet is 275 m/s. (b) Discuss
qualitatively how a larger muzzle velocity would affect this problem and
what would be the effect of air resistance.
40.
An eagle is flying horizontally at a speed of 3.00 m/s when the fish inher talons wiggles loose and falls into the lake 5.00 m below. Calculate
the velocity of the fish relative to the water when it hits the water.
41.
An owl is carrying a mouse to the chicks in its nest. Its position at thattime is 4.00 m west and 12.0 m above the center of the 30.0 cm diameter
nest. The owl is flying east at 3.50 m/s at an angle
30.0º below thehorizontal when it accidentally drops the mouse. Is the owl lucky enough
to have the mouse hit the nest? To answer this question, calculate the
horizontal position of the mouse when it has fallen 12.0 m.
42.
Suppose a soccer player kicks the ball from a distance 30 m towardthe goal. Find the initial speed of the ball if it just passes over the goal,
2.4 m above the ground, given the initial direction to be
40º above thehorizontal.
43.
Can a goalkeeper at her/ his goal kick a soccer ball into theopponent’s goal without the ball touching the ground? The distance will
be about 95 m. A goalkeeper can give the ball a speed of 30 m/s.
120 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
44.
The free throw line in basketball is 4.57 m (15 ft) from the basket,which is 3.05 m (10 ft) above the floor. A player standing on the free
throw line throws the ball with an initial speed of 7.15 m/s, releasing it at
a height of 2.44 m (8 ft) above the floor. At what angle above the
horizontal must the ball be thrown to exactly hit the basket? Note that
most players will use a large initial angle rather than a flat shot because it
allows for a larger margin of error. Explicitly show how you follow the
steps involved in solving projectile motion problems.
45.
In 2007, Michael Carter (U.S.) set a world record in the shot put witha throw of 24.77 m. What was the initial speed of the shot if he released it
at a height of 2.10 m and threw it at an angle of
38.0º above thehorizontal? (Although the maximum distance for a projectile on level
ground is achieved at
45º when air resistance is neglected, the actualangle to achieve maximum range is smaller; thus,
38º will give a longerrange than
45º in the shot put.)46.
A basketball player is running at 5.00 m/s directly toward the basketwhen he jumps into the air to dunk the ball. He maintains his horizontal
velocity. (a) What vertical velocity does he need to rise 0.750 m above
the floor? (b) How far from the basket (measured in the horizontal
direction) must he start his jump to reach his maximum height at the
same time as he reaches the basket?
47.
A football player punts the ball at a 45.0º angle. Without an effectfrom the wind, the ball would travel 60.0 m horizontally. (a) What is the
initial speed of the ball? (b) When the ball is near its maximum height it
experiences a brief gust of wind that reduces its horizontal velocity by
1.50 m/s. What distance does the ball travel horizontally?
48.
Prove that the trajectory of a projectile is parabolic, having the formy
= ax + bx2 . To obtain this expression, solve the equation x = v0x tfor
t and substitute it into the expression for y = v0yt – (1 / 2)gt2(These equations describe the
x and y positions of a projectile thatstarts at the origin.) You should obtain an equation of the form
y
= ax + bx2 where a and b are constants.49.
Derive R = v0 2 sin 2θ0 g for the range of a projectile on level groundby finding the time
t at which y becomes zero and substituting thisvalue of
t into the expression for x − x0 , noting that R = x − x050. Unreasonable Results
(a) Find the maximum range of a supercannon that has a muzzle velocity of 4.0 km/s. (b) What is unreasonable
about the range you found? (c) Is the premise unreasonable or is the
available equation inapplicable? Explain your answer. (d) If such a
muzzle velocity could be obtained, discuss the effects of air resistance,
thinning air with altitude, and the curvature of the Earth on the range of
the super cannon.
51. Construct Your Own Problem
Consider a ball tossed over a fence.Construct a problem in which you calculate the ball’s needed initial
velocity to just clear the fence. Among the things to determine are; the
height of the fence, the distance to the fence from the point of release of
the ball, and the height at which the ball is released. You should also
consider whether it is possible to choose the initial speed for the ball and
just calculate the angle at which it is thrown. Also examine the possibility
of multiple solutions given the distances and heights you have chosen.
3.5 Addition of Velocities
52.
Bryan Allen pedaled a human-powered aircraft across the EnglishChannel from the cliffs of Dover to Cap Gris-Nez on June 12, 1979. (a)
He flew for 169 min at an average velocity of 3.53 m/s in a direction
45ºsouth of east. What was his total displacement? (b) Allen encountered a
headwind averaging 2.00 m/s almost precisely in the opposite direction of
his motion relative to the Earth. What was his average velocity relative to
the air? (c) What was his total displacement relative to the air mass?
53.
A seagull flies at a velocity of 9.00 m/s straight into the wind. (a) If ittakes the bird 20.0 min to travel 6.00 km relative to the Earth, what is the
velocity of the wind? (b) If the bird turns around and flies with the wind,
how long will he take to return 6.00 km? (c) Discuss how the wind affects
the total round-trip time compared to what it would be with no wind.
54.
Near the end of a marathon race, the first two runners are separatedby a distance of 45.0 m. The front runner has a velocity of 3.50 m/s, and
the second a velocity of 4.20 m/s. (a) What is the velocity of the second
runner relative to the first? (b) If the front runner is 250 m from the finish
line, who will win the race, assuming they run at constant velocity? (c)
What distance ahead will the winner be when she crosses the finish line?
55.
Verify that the coin dropped by the airline passenger in the Example3.8
travels 144 m horizontally while falling 1.50 m in the frame ofreference of the Earth.
56.
A football quarterback is moving straight backward at a speed of 2.00m/s when he throws a pass to a player 18.0 m straight downfield. The
ball is thrown at an angle of
25.0º relative to the ground and is caught atthe same height as it is released. What is the initial velocity of the ball
relative to the quarterback
?57.
A ship sets sail from Rotterdam, The Netherlands, heading due northat 7.00 m/s relative to the water. The local ocean current is 1.50 m/s in a
direction
40.0º north of east. What is the velocity of the ship relative tothe Earth?
58.
A jet airplane flying from Darwin, Australia, has an air speed of 260m/s in a direction
5.0º south of west. It is in the jet stream, which isblowing at 35.0 m/s in a direction
15º south of east. What is the velocityof the airplane relative to the Earth? (b) Discuss whether your answers
are consistent with your expectations for the effect of the wind on the
plane’s path.
59.
(a) In what direction would the ship in Exercise 3.57 have to travel inorder to have a velocity straight north relative to the Earth, assuming its
speed relative to the water remains
7.00 m/s ? (b) What would its speedbe relative to the Earth?
60.
(a) Another airplane is flying in a jet stream that is blowing at 45.0 m/sin a direction
20º south of east (as in Exercise 3.58). Its direction ofmotion relative to the Earth is
45.0º south of west, while its direction oftravel relative to the air is
5.00º south of west. What is the airplane’sspeed relative to the air mass? (b) What is the airplane’s speed relative
to the Earth?
61.
A sandal is dropped from the top of a 15.0-m-high mast on a shipmoving at 1.75 m/s due south. Calculate the velocity of the sandal when
it hits the deck of the ship: (a) relative to the ship and (b) relative to a
stationary observer on shore. (c) Discuss how the answers give a
consistent result for the position at which the sandal hits the deck.
62.
The velocity of the wind relative to the water is crucial to sailboats.Suppose a sailboat is in an ocean current that has a velocity of 2.20 m/s
in a direction
30.0º east of north relative to the Earth. It encounters awind that has a velocity of 4.50 m/s in a direction of
50.0º south of westrelative to the Earth. What is the velocity of the wind relative to the water?
63.
The great astronomer Edwin Hubble discovered that all distantgalaxies are receding from our Milky Way Galaxy with velocities
proportional to their distances. It appears to an observer on the Earth that
we are at the center of an expanding universe.
Figure 3.64 illustrates thisfor five galaxies lying along a straight line, with the Milky Way Galaxy at
the center. Using the data from the figure, calculate the velocities: (a)
relative to galaxy 2 and (b) relative to galaxy 5. The results mean that
observers on all galaxies will see themselves at the center of the
expanding universe, and they would likely be aware of relative velocities,
concluding that it is not possible to locate the center of expansion with
the given information.
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 121
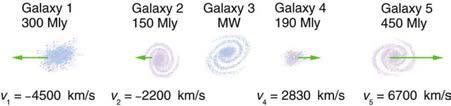
Figure 3.64
Five galaxies on a straight line, showing their distances and velocitiesrelative to the Milky Way (MW) Galaxy. The distances are in millions of light years
(Mly), where a light year is the distance light travels in one year. The velocities are
nearly proportional to the distances. The sizes of the galaxies are greatly
exaggerated; an average galaxy is about 0.1 Mly across.
64.
(a) Use the distance and velocity data in Figure 3.64 to find the rateof expansion as a function of distance.
(b) If you extrapolate back in time, how long ago would all of the galaxies
have been at approximately the same position? The two parts of this
problem give you some idea of how the Hubble constant for universal
expansion and the time back to the Big Bang are determined,
respectively.
65.
An athlete crosses a 25-m-wide river by swimming perpendicular tothe water current at a speed of 0.5 m/s relative to the water. He reaches
the opposite side at a distance 40 m downstream from his starting point.
How fast is the water in the river flowing with respect to the ground?
What is the speed of the swimmer with respect to a friend at rest on the
ground?
66.
A ship sailing in the Gulf Stream is heading 25.0º west of north at aspeed of 4.00 m/s relative to the water. Its velocity relative to the Earth is
4.80 m/s 5.00º
west of north. What is the velocity of the Gulf Stream?(The velocity obtained is typical for the Gulf Stream a few hundred
kilometers off the east coast of the United States.)
67.
An ice hockey player is moving at 8.00 m/s when he hits the pucktoward the goal. The speed of the puck relative to the player is 29.0 m/s.
The line between the center of the goal and the player makes a
90.0ºangle relative to his path as shown in
Figure 3.65. What angle must thepuck’s velocity make relative to the player (in his frame of reference) to
hit the center of the goal?
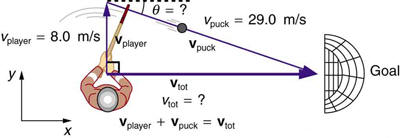
Figure 3.65
An ice hockey player moving across the rink must shoot backward to givethe puck a velocity toward the goal.
68. Unreasonable Results
Suppose you wish to shoot supplies straightup to astronauts in an orbit 36,000 km above the surface of the Earth. (a)
At what velocity must the supplies be launched? (b) What is
unreasonable about this velocity? (c) Is there a problem with the relative
velocity between the supplies and the astronauts when the supplies
reach their maximum height? (d) Is the premise unreasonable or is the
available equation inapplicable? Explain your answer.
69. Unreasonable Results
A commercial airplane has an air speed of280 m/s
due east and flies with a strong tailwind. It travels 3000 km in adirection
5º south of east in 1.50 h. (a) What was the velocity of theplane relative to the ground? (b) Calculate the magnitude and direction of
the tailwind’s velocity. (c) What is unreasonable about both of these
velocities? (d) Which premise is unreasonable?
70. Construct Your Own Problem
Consider an airplane headed for arunway in a cross wind. Construct a problem in which you calculate the
angle the airplane must fly relative to the air mass in order to have a
velocity parallel to the runway. Among the things to consider are the
direction of the runway, the wind speed and direction (its velocity) and the
speed of the plane relative to the air mass. Also calculate the speed of
the airplane relative to the ground. Discuss any last minute maneuvers
the pilot might have to perform in order for the
4.3 Newton’s Second Law of Motion: Concept of a
System
You may assume data taken from illustrations is accurate to three
digits.
prin, gen: 1.
A 63.0-kg sprinter starts a race with an acceleration of 4.20 m/s2 .What is the net external force on him?
prin, gen: 1a. A bicycle and its rider experience a net force of 250 N, which accelerates them at 2.3 m/s^2. What is the total mass of the bicycle and its rider?
2.
If the sprinter from the previous problem accelerates at that rate for 20m, and then maintains that velocity for the remainder of the 100-m dash,
what will be his time for the race?
prin: 3.
A cleaner pushes a 4.50-kg laundry cart in such a way that the netexternal force on it is 60.0 N. Calculate its acceleration.
gen: 4.
Since astronauts in orbit are apparently weightless, a clever method ofmeasuring their masses is needed to monitor their mass gains or losses
to adjust diets. One way to do this is to exert a known force on an
astronaut and measure the acceleration produced. Suppose a net
external force of 50.0 N is exerted and the astronaut’s acceleration is
measured to be
0.893 m/s2 . (a) Calculate her mass. (b) By exerting aforce on the astronaut, the vehicle in which they orbit experiences an
equal and opposite force. Discuss how this would affect the
measurement of the astronaut’s acceleration. Propose a method in which
recoil of the vehicle is avoided.
prin: 5.
In Figure 4.7, the net external force on the 24-kg mower is stated to be51 N. If the force of friction opposing the motion is 24 N, what force
F (innewtons) is the person exerting on the mower? Suppose the mower is
moving at 1.5 m/s when the force
F is removed. How far will the mowergo before stopping?
6.
The same rocket sled drawn in Figure 4.31 is decelerated at a rate of196 m/s
2 . What force is necessary to produce this deceleration?Assume that the rockets are off. The mass of the system is 2100 kg.
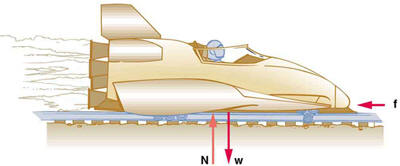
Figure 4.31
7.
(a) If the rocket sled shown in Figure 4.32 starts with only one rocketburning, what is its acceleration? Assume that the mass of the system is
2100 kg, and the force of friction opposing the motion is known to be 650
N. (b) Why is the acceleration not one-fourth of what it is with all rockets
burning?

Figure 4.32
8.
What is the deceleration of the rocket sled if it comes to rest in 1.1 sfrom a speed of 1000 km/h? (Such deceleration caused one test subject
to black out and have temporary blindness.)
gen: 9.
Suppose two children push horizontally, but in exactly oppositedirections, on a third child in a wagon. The first child exerts a force of
75.0 N, the second a force of 90.0 N, friction is 12.0 N, and the mass of
the third child plus wagon is 23.0 kg. (a) What is the system of interest if
the acceleration of the child in the wagon is to be calculated? (b) Draw a
free-body diagram, including all forces acting on the system. (c) Calculate
the acceleration. (d) What would the acceleration be if friction were 15.0
N?
prin: 10.
A powerful motorcycle can produce an acceleration of 3.50 m/s2while traveling at 90.0 km/h. At that speed the forces resisting motion,
including friction and air resistance, total 400 N. (Air resistance is
analogous to air friction. It always opposes the motion of an object.) What
force does the motorcycle exert backward on the ground to produce its
acceleration if the mass of the motorcycle with rider is 245 kg?
prin, gen: 10a. What is the force required to accelerate a 10 gram pellet from rest to a velocity of 100 m/s in a rifle barrel 0.6 cm long?
gen: 10b. A fish is being pulled upward. The breaking strength of the line holding the fish is 22 N. An acceleration of 2.5 m/s^2 breaks the line. What can we say about the mass of the fish?
11.
The rocket sled shown in Figure 4.33 accelerates at a rate of49.0 m/s
2 . Its passenger has a mass of 75.0 kg. (a) Calculate thehorizontal component of the force the seat exerts against his body.
Compare this with his weight by using a ratio. (b) Calculate the direction
and magnitude of the total force the seat exerts against his body.
 Figure
4.33
Figure
4.33
12.
Repeat the previous problem for the situation in which the rocket sleddecelerates at a rate of
201 m/s2 . In this problem, the forces areexerted by the seat and restraining belts.
gen: 13.
The weight of an astronaut plus his space suit on the Moon is only250 N. How much do they weigh on Earth? What is the mass on the
Moon? On Earth?
14.
Suppose the mass of a fully loaded module in which astronauts takeoff from the Moon is 10,000 kg. The thrust of its engines is 30,000 N. (a)
Calculate its acceleration in a vertical takeoff from the Moon. (b) Could it
lift off from Earth? If not, why not? If it could, calculate its acceleration.
4.4 Newton’s Third Law of Motion: Symmetry in Forces
15.
What net external force is exerted on a 1100-kg artillery shell firedfrom a battleship if the shell is accelerated at
2.40×104 m/s2 ? Whatforce is exerted on the ship by the artillery shell?
16.
A brave but inadequate rugby player is being pushed backward by anopposing player who is exerting a force of 800 N on him. The mass of the
losing player plus equipment is 90.0 kg, and he is accelerating at
1.20 m/s
2 backward. (a) What is the force of friction between the losingplayer’s feet and the grass? (b) What force does the winning player exert
on the ground to move forward if his mass plus equipment is 110 kg? (c)
Draw a sketch of the situation showing the system of interest used to
solve each part. For this situation, draw a free-body diagram and write
the net force equation.
4.5 Normal, Tension, and Other Examples of Forces
17.
Two teams of nine members each engage in a tug of war. Each of thefirst team’s members has an average mass of 68 kg and exerts an
average force of 1350 N horizontally. Each of the second team’s
members has an average mass of 73 kg and exerts an average force of
1365 N horizontally. (a) What is the acceleration of the two teams? (b)
What is the tension in the section of rope between the teams?
18.
What force does a trampoline have to apply to a 45.0-kg gymnast toaccelerate her straight up at
7.50 m/s2 ? Note that the answer isindependent of the velocity of the gymnast—she can be moving either up
or down, or be stationary.
19.
(a) Calculate the tension in a vertical strand of spider web if a spiderof mass
8.00×10−5 kg hangs motionless on it. (b) Calculate thetension in a horizontal strand of spider web if the same spider sits
motionless in the middle of it much like the tightrope walker in
Figure156 CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION
4.17
. The strand sags at an angle of 12º below the horizontal. Comparethis with the tension in the vertical strand (find their ratio).
20.
Suppose a 60.0-kg gymnast climbs a rope. (a) What is the tension inthe rope if he climbs at a constant speed? (b) What is the tension in the
rope if he accelerates upward at a rate of
1.50 m/s2 ?21.
Show that, as stated in the text, a force F⊥ exerted on a flexiblemedium at its center and perpendicular to its length (such as on the
tightrope wire in
Figure 4.17) gives rise to a tension of magnitudeT
= F⊥2 sin (
θ) .22.
Consider the baby being weighed in Figure 4.34. (a) What is themass of the child and basket if a scale reading of 55 N is observed? (b)
What is the tension
T1 in the cord attaching the baby to the scale? (c)What is the tension
T2 in the cord attaching the scale to the ceiling, ifthe scale has a mass of 0.500 kg? (d) Draw a sketch of the situation
indicating the system of interest used to solve each part. The masses of
the cords are negligible.
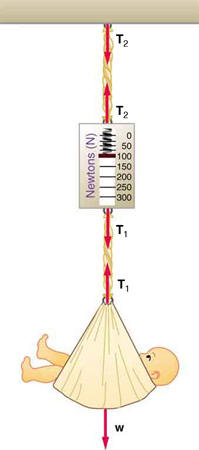
Figure 4.34
A baby is weighed using a spring scale.4.6 Problem-Solving Strategies
23.
A 5.00×105-kg rocket is accelerating straight up. Its enginesproduce
1.250×107 N of thrust, and air resistance is 4.50×106 N .What is the rocket’s acceleration? Explicitly show how you follow the
steps in the Problem-Solving Strategy for Newton’s laws of motion.
24.
The wheels of a midsize car exert a force of 2100 N backward on theroad to accelerate the car in the forward direction. If the force of friction
including air resistance is 250 N and the acceleration of the car is
1.80 m/s
2 , what is the mass of the car plus its occupants? Explicitlyshow how you follow the steps in the Problem-Solving Strategy for
Newton’s laws of motion. For this situation, draw a free-body diagram
and write the net force equation.
25.
Calculate the force a 70.0-kg high jumper must exert on the ground toproduce an upward acceleration 4.00 times the acceleration due to
gravity. Explicitly show how you follow the steps in the Problem-Solving
Strategy for Newton’s laws of motion.
25b: A person of mass 66 kg crouches then jumps to a height of .8 meters. From the crouched position to the point where the person leaves the ground the distance is 20 cm. What average force is exerted over this 20-cm distance?
26.
When landing after a spectacular somersault, a 40.0-kg gymnastdecelerates by pushing straight down on the mat. Calculate the force she
must exert if her deceleration is 7.00 times the acceleration due to
gravity. Explicitly show how you follow the steps in the Problem-Solving
Strategy for Newton’s laws of motion.
27.
A freight train consists of two 8.00×104 -kg engines and 45 carswith average masses of
5.50×104 kg . (a) What force must eachengine exert backward on the track to accelerate the train at a rate of
5.00×10
–2 m/s2 if the force of friction is 7.50×105 N , assuming theengines exert identical forces? This is not a large frictional force for such
a massive system. Rolling friction for trains is small, and consequently
trains are very energy-efficient transportation systems. (b) What is the
force in the coupling between the 37th and 38th cars (this is the force
each exerts on the other), assuming all cars have the same mass and
that friction is evenly distributed among all of the cars and engines?
28.
Commercial airplanes are sometimes pushed out of the passengerloading area by a tractor. (a) An 1800-kg tractor exerts a force of
1.75×10
4 N backward on the pavement, and the system experiencesforces resisting motion that total 2400 N. If the acceleration is
0.150 m/s
2 , what is the mass of the airplane? (b) Calculate the forceexerted by the tractor on the airplane, assuming 2200 N of the friction is
experienced by the airplane. (c) Draw two sketches showing the systems
of interest used to solve each part, including the free-body diagrams for
each.
29.
A 1100-kg car pulls a boat on a trailer. (a) What total force resists themotion of the car, boat, and trailer, if the car exerts a 1900-N force on the
road and produces an acceleration of
0.550 m/s2 ? The mass of theboat plus trailer is 700 kg. (b) What is the force in the hitch between the
car and the trailer if 80% of the resisting forces are experienced by the
boat and trailer?
30.
(a) Find the magnitudes of the forces F1 and F2 that add to givethe total force
Ftot shown in Figure 4.35. This may be done eithergraphically or by using trigonometry. (b) Show graphically that the same
total force is obtained independent of the order of addition of
F1 andF
2 . (c) Find the direction and magnitude of some other pair of vectorsthat add to give
Ftot . Draw these to scale on the same drawing used inpart (b) or a similar picture.
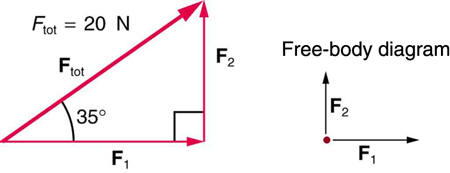
Figure 4.35
31.
Two children pull a third child on a snow saucer sled exerting forcesF
1 and F2 as shown from above in Figure 4.36. Find the accelerationof the 49.00-kg sled and child system. Note that the direction of the
frictional force is unspecified; it will be in the opposite direction of the sum
of
F1 and F2 .CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION 157
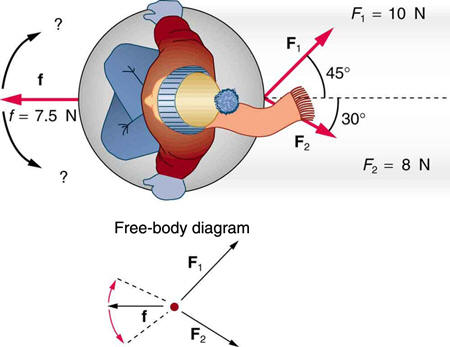 Figure
4.36
Figure
4.36
sled.
32.
Suppose your car was mired deeply in the mud and you wanted touse the method illustrated in
Figure 4.37 to pull it out. (a) What forcewould you have to exert perpendicular to the center of the rope to
produce a force of 12,000 N on the car if the angle is 2.00°? In this part,
explicitly show how you follow the steps in the Problem-Solving Strategy
for Newton’s laws of motion. (b) Real ropes stretch under such forces.
What force would be exerted on the car if the angle increases to 7.00°
and you still apply the force found in part (a) to its center?

Figure 4.37
33.
What force is exerted on the tooth in Figure 4.38 if the tension in thewire is 25.0 N? Note that the force applied to the tooth is smaller than the
tension in the wire, but this is necessitated by practical considerations of
how force can be applied in the mouth. Explicitly show how you follow
steps in the Problem-Solving Strategy for Newton’s laws of motion.
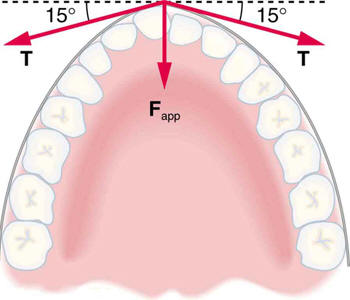
Figure 4.38
Braces are used to apply forces to teeth to realign them. Shown in thisfigure are the tensions applied by the wire to the protruding tooth. The total force
applied to the tooth by the wire,
Fapp , points straight toward the back of the mouth.34.
Figure 4.39 shows Superhero and Trusty Sidekick hangingmotionless from a rope. Superhero’s mass is 90.0 kg, while Trusty
Sidekick’s is 55.0 kg, and the mass of the rope is negligible. (a) Draw a
free-body diagram of the situation showing all forces acting on
Superhero, Trusty Sidekick, and the rope. (b) Find the tension in the rope
above Superhero. (c) Find the tension in the rope between Superhero
and Trusty Sidekick. Indicate on your free-body diagram the system of
interest used to solve each part.

Figure 4.39
Superhero and Trusty Sidekick hang motionless on a rope as they try tofigure out what to do next. Will the tension be the same everywhere in the rope?
35.
A nurse pushes a cart by exerting a force on the handle at adownward angle
35.0º below the horizontal. The loaded cart has amass of 28.0 kg, and the force of friction is 60.0 N. (a) Draw a free-body
diagram for the system of interest. (b) What force must the nurse exert to
move at a constant velocity?
36. Construct Your Own Problem
Consider the tension in an elevatorcable during the time the elevator starts from rest and accelerates its load
upward to some cruising velocity. Taking the elevator and its load to be
the system of interest, draw a free-body diagram. Then calculate the
tension in the cable. Among the things to consider are the mass of the
elevator and its load, the final velocity, and the time taken to reach that
velocity.
37. Construct Your Own Problem
Consider two people pushing atoboggan with four children on it up a snow-covered slope. Construct a
problem in which you calculate the acceleration of the toboggan and its
load. Include a free-body diagram of the appropriate system of interest as
the basis for your analysis. Show vector forces and their components and
explain the choice of coordinates. Among the things to be considered are
the forces exerted by those pushing, the angle of the slope, and the
masses of the toboggan and children.
38. Unreasonable Results
(a) Repeat Exercise 4.29, but assume anacceleration of
1.20 m/s2 is produced. (b) What is unreasonable aboutthe result? (c) Which premise is unreasonable, and why is it
unreasonable?
39. Unreasonable Results
(a) What is the initial acceleration of a rocketthat has a mass of
1.50×106 kg at takeoff, the engines of whichproduce a thrust of
2.00×106 N ? Do not neglect gravity. (b) What isunreasonable about the result? (This result has been unintentionally
achieved by several real rockets.) (c) Which premise is unreasonable, or
which premises are inconsistent? (You may find it useful to compare this
problem to the rocket problem earlier in this section.)
158 CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION
4.7 Further Applications of Newton’s Laws of Motion
40.
A flea jumps by exerting a force of 1.20×10−5 N straight down onthe ground. A breeze blowing on the flea parallel to the ground exerts a
force of
0.500×10−6 N on the flea. Find the direction and magnitudeof the acceleration of the flea if its mass is
6.00×10−7 kg . Do notneglect the gravitational force.
41.
Two muscles in the back of the leg pull upward on the Achillestendon, as shown in
Figure 4.40. (These muscles are called the medialand lateral heads of the gastrocnemius muscle.) Find the magnitude and
direction of the total force on the Achilles tendon. What type of movement
could be caused by this force?
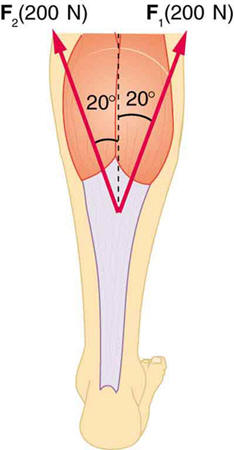
Figure 4.40
Achilles tendon42.
A 76.0-kg person is being pulled away from a burning building asshown in
Figure 4.41. Calculate the tension in the two ropes if the personis momentarily motionless. Include a free-body diagram in your solution.
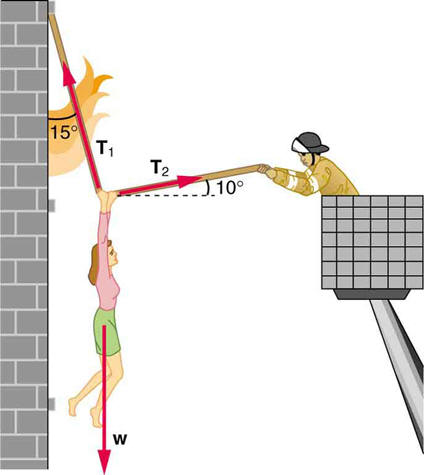
Figure 4.41
The force T2 needed to hold steady the person being rescued from thefire is less than her weight and less than the force
T1 in the other rope, since themore vertical rope supports a greater part of her weight (a vertical force).
43. Integrated Concepts
A 35.0-kg dolphin decelerates from 12.0 to7.50 m/s in 2.30 s to join another dolphin in play. What average force was
exerted to slow him if he was moving horizontally? (The gravitational
force is balanced by the buoyant force of the water.)
44. Integrated Concepts
When starting a foot race, a 70.0-kg sprinterexerts an average force of 650 N backward on the ground for 0.800 s. (a)
What is his final speed? (b) How far does he travel?
45. Integrated Concepts
A large rocket has a mass of 2.00×106 kg attakeoff, and its engines produce a thrust of
3.50×107 N . (a) Find itsinitial acceleration if it takes off vertically. (b) How long does it take to
reach a velocity of 120 km/h straight up, assuming constant mass and
thrust? (c) In reality, the mass of a rocket decreases significantly as its
fuel is consumed. Describe qualitatively how this affects the acceleration
and time for this motion.
46. Integrated Concepts
A basketball player jumps straight up for a ball.To do this, he lowers his body 0.300 m and then accelerates through this
distance by forcefully straightening his legs. This player leaves the floor
with a vertical velocity sufficient to carry him 0.900 m above the floor. (a)
Calculate his velocity when he leaves the floor. (b) Calculate his
acceleration while he is straightening his legs. He goes from zero to the
velocity found in part (a) in a distance of 0.300 m. (c) Calculate the force
he exerts on the floor to do this, given that his mass is 110 kg.
47. Integrated Concepts
A 2.50-kg fireworks shell is fired straight upfrom a mortar and reaches a height of 110 m. (a) Neglecting air
resistance (a poor assumption, but we will make it for this example),
calculate the shell’s velocity when it leaves the mortar. (b) The mortar
itself is a tube 0.450 m long. Calculate the average acceleration of the
shell in the tube as it goes from zero to the velocity found in (a). (c) What
is the average force on the shell in the mortar? Express your answer in
newtons and as a ratio to the weight of the shell.
48. Integrated Concepts
Repeat Exercise 4.47 for a shell fired at anangle
10.0º from the vertical.49. Integrated Concepts
An elevator filled with passengers has a massof 1700 kg. (a) The elevator accelerates upward from rest at a rate of
1.20 m/s
2 for 1.50 s. Calculate the tension in the cable supporting theelevator. (b) The elevator continues upward at constant velocity for 8.50
s. What is the tension in the cable during this time? (c) The elevator
decelerates at a rate of
0.600 m/s2 for 3.00 s. What is the tension inCHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION 159
the cable during deceleration? (d) How high has the elevator moved
above its original starting point, and what is its final velocity?
50. Unreasonable Results
(a) What is the final velocity of a car originallytraveling at 50.0 km/h that decelerates at a rate of
0.400 m/s2 for 50.0s? (b) What is unreasonable about the result? (c) Which premise is
unreasonable, or which premises are inconsistent?
51. Unreasonable Results
A 75.0-kg man stands on a bathroom scalein an elevator that accelerates from rest to 30.0 m/s in 2.00 s. (a)
Calculate the scale reading in newtons and compare it with his weight.
(The scale exerts an upward force on him equal to its reading.) (b) What
is unreasonable about the result? (c) Which premise is unreasonable, or
which premises are inconsistent?
4.8 Extended Topic: The Four Basic Forces—An
Introduction
52.
(a) What is the strength of the weak nuclear force relative to thestrong nuclear force? (b) What is the strength of the weak nuclear force
relative to the electromagnetic force? Since the weak nuclear force acts
at only very short distances, such as inside nuclei, where the strong and
electromagnetic forces also act, it might seem surprising that we have
any knowledge of it at all. We have such knowledge because the weak
nuclear force is
5.1 Friction
1.
A physics major is cooking breakfast when he notices that the frictionalforce between his steel spatula and his Teflon frying pan is only 0.200 N.
Knowing the coefficient of kinetic friction between the two materials, he
quickly calculates the normal force. What is it?
2.
(a) When rebuilding her car’s engine, a physics major must exert 300N of force to insert a dry steel piston into a steel cylinder. What is the
normal force between the piston and cylinder? (b) What force would she
have to exert if the steel parts were oiled?
3.
(a) What is the maximum frictional force in the knee joint of a personwho supports 66.0 kg of her mass on that knee? (b) During strenuous
exercise it is possible to exert forces to the joints that are easily ten times
greater than the weight being supported. What is the maximum force of
friction under such conditions? The frictional forces in joints are relatively
small in all circumstances except when the joints deteriorate, such as
from injury or arthritis. Increased frictional forces can cause further
damage and pain.
4.
Suppose you have a 120-kg wooden crate resting on a wood floor. (a)What maximum force can you exert horizontally on the crate without
moving it? (b) If you continue to exert this force once the crate starts to
slip, what will its acceleration then be?
5.
(a) If half of the weight of a small 1.00×103 kg utility truck issupported by its two drive wheels, what is the maximum acceleration it
can achieve on dry concrete? (b) Will a metal cabinet lying on the
wooden bed of the truck slip if it accelerates at this rate? (c) Solve both
problems assuming the truck has four-wheel drive.
6.
A team of eight dogs pulls a sled with waxed wood runners on wetsnow (mush!). The dogs have average masses of 19.0 kg, and the
loaded sled with its rider has a mass of 210 kg. (a) Calculate the
acceleration starting from rest if each dog exerts an average force of 185
N backward on the snow. (b) What is the acceleration once the sled
starts to move? (c) For both situations, calculate the force in the coupling
between the dogs and the sled.
7.
Consider the 65.0-kg ice skater being pushed by two others shown inFigure 5.21
. (a) Find the direction and magnitude of Ftot , the total forceexerted on her by the others, given that the magnitudes
F1 and F2 are26.4 N and 18.6 N, respectively. (b) What is her initial acceleration if she
is initially stationary and wearing steel-bladed skates that point in the
direction of
Ftot ? (c) What is her acceleration assuming she is alreadymoving in the direction of
Ftot ? (Remember that friction always acts inthe direction opposite that of motion or attempted motion between
surfaces in contact.)
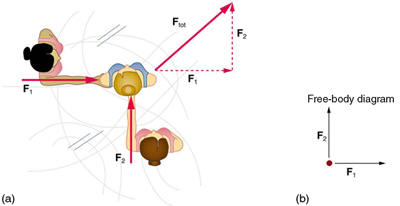
Figure 5.21
8.
Show that the acceleration of any object down a frictionless incline thatmakes an angle
θ with the horizontal is a = g sin θ . (Note that thisacceleration is independent of mass.)
9.
Show that the acceleration of any object down an incline where frictionbehaves simply (that is, where
fk = μkN ) isa
= g( sin θ − μkcos θ). Note that the acceleration is independent ofmass and reduces to the expression found in the previous problem when
friction becomes negligibly small
(μk = 0).10.
Calculate the deceleration of a snow boarder going up a 5.0º , slopeassuming the coefficient of friction for waxed wood on wet snow. The
result of
Exercise 5.1 may be useful, but be careful to consider the factthat the snow boarder is going uphill. Explicitly show how you follow the
steps in
Problem-Solving Strategies.11.
(a) Calculate the acceleration of a skier heading down a 10.0º slope,assuming the coefficient of friction for waxed wood on wet snow. (b) Find
the angle of the slope down which this skier could coast at a constant
velocity. You can neglect air resistance in both parts, and you will find the
result of
Exercise 5.1 to be useful. Explicitly show how you follow thesteps in the
Problem-Solving Strategies.12.
If an object is to rest on an incline without slipping, then friction mustequal the component of the weight of the object parallel to the incline.
This requires greater and greater friction for steeper slopes. Show that
the maximum angle of an incline above the horizontal for which an object
will not slide down is
θ = tan–1 μs . You may use the result of theprevious problem. Assume that
a = 0 and that static friction hasreached its maximum value.
13.
Calculate the maximum deceleration of a car that is heading down a6º
slope (one that makes an angle of 6º with the horizontal) under thefollowing road conditions. You may assume that the weight of the car is
evenly distributed on all four tires and that the coefficient of static friction
is involved—that is, the tires are not allowed to slip during the
deceleration. (Ignore rolling.) Calculate for a car: (a) On dry concrete. (b)
On wet concrete. (c) On ice, assuming that
μs = 0.100 , the same asfor shoes on ice.
14.
Calculate the maximum acceleration of a car that is heading up a 4ºslope (one that makes an angle of
4º with the horizontal) under thefollowing road conditions. Assume that only half the weight of the car is
supported by the two drive wheels and that the coefficient of static friction
is involved—that is, the tires are not allowed to slip during the
acceleration. (Ignore rolling.) (a) On dry concrete. (b) On wet concrete.
(c) On ice, assuming that
μs = 0.100 , the same as for shoes on ice.15.
Repeat Exercise 5.2 for a car with four-wheel drive.16.
A freight train consists of two 8.00×105-kg engines and 45 carswith average masses of
5.50×105 kg . (a) What force must eachengine exert backward on the track to accelerate the train at a rate of
5.00×10
−2 m / s2 if the force of friction is 7.50×105 N , assumingthe engines exert identical forces? This is not a large frictional force for
such a massive system. Rolling friction for trains is small, and
consequently trains are very energy-efficient transportation systems. (b)
What is the force in the coupling between the 37th and 38th cars (this is
the force each exerts on the other), assuming all cars have the same
mass and that friction is evenly distributed among all of the cars and
engines?
17.
Consider the 52.0-kg mountain climber in Figure 5.22. (a) Find thetension in the rope and the force that the mountain climber must exert
with her feet on the vertical rock face to remain stationary. Assume that
the force is exerted parallel to her legs. Also, assume negligible force
exerted by her arms. (b) What is the minimum coefficient of friction
between her shoes and the cliff?
CHAPTER 5 | FURTHER APPLICATIONS OF NEWTON'S LAWS: FRICTION, DRAG, AND ELASTICITY 181
 Figure
5.22
Figure
5.22
between her feet and the rock face.
18.
A contestant in a winter sporting event pushes a 45.0-kg block of iceacross a frozen lake as shown in
Figure 5.23(a). (a) Calculate theminimum force
F he must exert to get the block moving. (b) What is itsacceleration once it starts to move, if that force is maintained?
19.
Repeat Exercise 5.3 with the contestant pulling the block of ice witha rope over his shoulder at the same angle above the horizontal as
shown in
Figure 5.23(b).
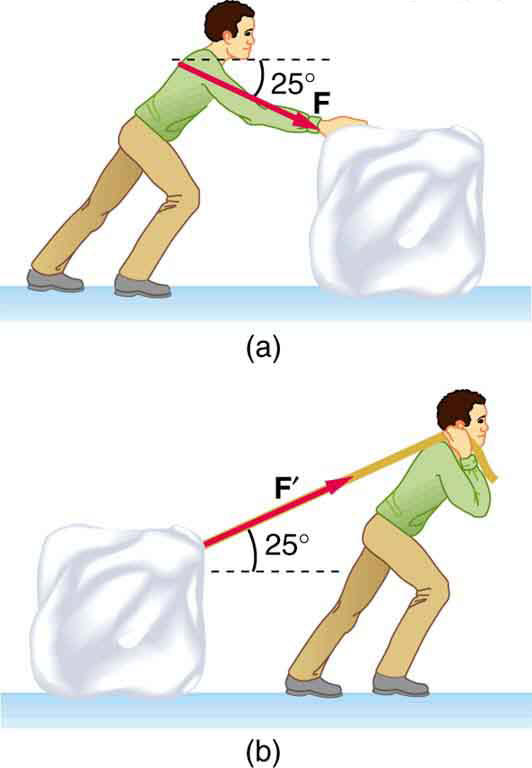
Figure 5.23
Which method of sliding a block of ice requires less force—(a) pushing or(b) pulling at the same angle above the horizontal?
5.2 Drag Forces
20.
The terminal velocity of a person falling in air depends upon theweight and the area of the person facing the fluid. Find the terminal
velocity (in meters per second and kilometers per hour) of an 80.0-kg
skydiver falling in a pike (headfirst) position with a surface area of
0.140 m
2 .21.
A 60-kg and a 90-kg skydiver jump from an airplane at an altitude of6000 m, both falling in the pike position. Make some assumption on their
frontal areas and calculate their terminal velocities. How long will it take
for each skydiver to reach the ground (assuming the time to reach
terminal velocity is small)? Assume all values are accurate to three
significant digits.
22.
A 560-g squirrel with a surface area of 930 cm2 falls from a 5.0-mtree to the ground. Estimate its terminal velocity. (Use a drag coefficient
for a horizontal skydiver.) What will be the velocity of a 56-kg person
hitting the ground, assuming no drag contribution in such a short
distance?
23.
To maintain a constant speed, the force provided by a car’s enginemust equal the drag force plus the force of friction of the road (the rolling
resistance). (a) What are the drag forces at 70 km/h and 100 km/h for a
Toyota Camry? (Drag area is
0.70 m2 ) (b) What is the drag force at 70km/h and 100 km/h for a Hummer H2? (Drag area is
2.44 m2 ) Assumeall values are accurate to three significant digits.
24.
By what factor does the drag force on a car increase as it goes from65 to 110 km/h?
25.
Calculate the velocity a spherical rain drop would achieve falling from5.00 km (a) in the absence of air drag (b) with air drag. Take the size
across of the drop to be 4 mm, the density to be
1.00×103 kg/m3 , andthe surface area to be
πr2 .26.
Using Stokes’ law, verify that the units for viscosity are kilograms permeter per second.
27.
Find the terminal velocity of a spherical bacterium (diameter2.00 μm
) falling in water. You will first need to note that the drag force isequal to the weight at terminal velocity. Take the density of the bacterium
to be
1.10×103 kg/m3 .28.
Stokes’ law describes sedimentation of particles in liquids and can beused to measure viscosity. Particles in liquids achieve terminal velocity
quickly. One can measure the time it takes for a particle to fall a certain
distance and then use Stokes’ law to calculate the viscosity of the liquid.
Suppose a steel ball bearing (density
7.8×103 kg/m3 , diameter3.0 mm
) is dropped in a container of motor oil. It takes 12 s to fall adistance of 0.60 m. Calculate the viscosity of the oil.
5.3 Elasticity: Stress and Strain
29.
During a circus act, one performer swings upside down hanging froma trapeze holding another, also upside-down, performer by the legs. If the
upward force on the lower performer is three times her weight, how much
do the bones (the femurs) in her upper legs stretch? You may assume
each is equivalent to a uniform rod 35.0 cm long and 1.80 cm in radius.
Her mass is 60.0 kg.
30.
During a wrestling match, a 150 kg wrestler briefly stands on onehand during a maneuver designed to perplex his already moribund
adversary. By how much does the upper arm bone shorten in length?
The bone can be represented by a uniform rod 38.0 cm in length and
2.10 cm in radius.
31.
(a) The “lead” in pencils is a graphite composition with a Young’smodulus of about
1×109 N / m2 . Calculate the change in length of thelead in an automatic pencil if you tap it straight into the pencil with a force
of 4.0 N. The lead is 0.50 mm in diameter and 60 mm long. (b) Is the
answer reasonable? That is, does it seem to be consistent with what you
have observed when using pencils?
32.
TV broadcast antennas are the tallest artificial structures on Earth. In1987, a 72.0-kg physicist placed himself and 400 kg of equipment at the
top of one 610-m high antenna to perform gravity experiments. By how
much was the antenna compressed, if we consider it to be equivalent to a
steel cylinder 0.150 m in radius?
33.
(a) By how much does a 65.0-kg mountain climber stretch her0.800-cm diameter nylon rope when she hangs 35.0 m below a rock
outcropping? (b) Does the answer seem to be consistent with what you
have observed for nylon ropes? Would it make sense if the rope were
actually a bungee cord?
182 CHAPTER 5 | FURTHER APPLICATIONS OF NEWTON'S LAWS: FRICTION, DRAG, AND ELASTICITY
34.
A 20.0-m tall hollow aluminum flagpole is equivalent in strength to asolid cylinder 4.00 cm in diameter. A strong wind bends the pole much as
a horizontal force of 900 N exerted at the top would. How far to the side
does the top of the pole flex?
35.
As an oil well is drilled, each new section of drill pipe supports its ownweight and that of the pipe and drill bit beneath it. Calculate the stretch in
a new 6.00 m length of steel pipe that supports 3.00 km of pipe having a
mass of 20.0 kg/m and a 100-kg drill bit. The pipe is equivalent in
strength to a solid cylinder 5.00 cm in diameter.
36.
Calculate the force a piano tuner applies to stretch a steel piano wire8.00 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long.
37.
A vertebra is subjected to a shearing force of 500 N. Find the sheardeformation, taking the vertebra to be a cylinder 3.00 cm high and 4.00
cm in diameter.
38.
A disk between vertebrae in the spine is subjected to a shearing forceof 600 N. Find its shear deformation, taking it to have the shear modulus
of
1×109 N / m2 . The disk is equivalent to a solid cylinder 0.700 cmhigh and 4.00 cm in diameter.
39.
When using a pencil eraser, you exert a vertical force of 6.00 N at adistance of 2.00 cm from the hardwood-eraser joint. The pencil is 6.00
mm in diameter and is held at an angle of
20.0º to the horizontal. (a) Byhow much does the wood flex perpendicular to its length? (b) How much
is it compressed lengthwise?
40.
To consider the effect of wires hung on poles, we take data fromExample 4.8
, in which tensions in wires supporting a traffic light werecalculated. The left wire made an angle
30.0º below the horizontal withthe top of its pole and carried a tension of 108 N. The 12.0 m tall hollow
aluminum pole is equivalent in strength to a 4.50 cm diameter solid
cylinder. (a) How far is it bent to the side? (b) By how much is it
compressed?
41.
A farmer making grape juice fills a glass bottle to the brim and caps ittightly. The juice expands more than the glass when it warms up, in such
a way that the volume increases by 0.2% (that is,
ΔV / V0 = 2×10−3 )relative to the space available. Calculate the force exerted by the juice
per square centimeter if its bulk modulus is
1.8×109 N/m2 , assumingthe bottle does not break. In view of your answer, do you think the bottle
will survive?
42.
(a) When water freezes, its volume increases by 9.05% (that is,Δ
V / V0 = 9.05×10−2 ). What force per unit area is water capable ofexerting on a container when it freezes? (It is acceptable to use the bulk
modulus of water in this problem.) (b) Is it surprising that such forces can
fracture engine blocks, boulders, and the like?
43.
This problem returns to the tightrope walker studied in Example 4.6,who created a tension of
3.94×103 N in a wire making an angle 5.0ºbelow the horizontal with each supporting pole. Calculate how much this
tension stretches the steel wire if it was originally 15 m long and 0.50 cm
in diameter.
44.
The pole in Figure 5.24 is at a 90.0º bend in a power line and istherefore subjected to more shear force than poles in straight parts of the
line. The tension in each line is
4.00×104 N , at the angles shown. Thepole is 15.0 m tall, has an 18.0 cm diameter, and can be considered to
have half the strength of hardwood. (a) Calculate the compression of the
pole. (b) Find how much it bends and in what direction. (c) Find the
tension in a guy wire used to keep the pole straight if it is attached to the
top of the pole at an angle of
30.0º with the vertical. (Clearly, the guywire must be in the opposite direction of the bend.)
Problems& Exercises
7.1 Work: The Scientific Definition
1.
How much work does a supermarket checkout attendant do on a canof soup he pushes 0.600 m horizontally with a force of 5.00 N? Express
your answer in joules and kilocalories.
2.
A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find thework done to accomplish this task.
3.
(a) Calculate the work done on a 1500-kg elevator car by its cable tolift it 40.0 m at constant speed, assuming friction averages 100 N. (b)
What is the work done on the lift by the gravitational force in this
process? (c) What is the total work done on the lift?
4.
Suppose a car travels 108 km at a speed of 30.0 m/s, and uses 2.0 galof gasoline. Only 30% of the gasoline goes into useful work by the force
that keeps the car moving at constant speed despite friction. (See
Table7.1
for the energy content of gasoline.) (a) What is the force exerted tokeep the car moving at constant speed? (b) If the required force is
directly proportional to speed, how many gallons will be used to drive 108
km at a speed of 28.0 m/s?
5.
Calculate the work done by an 75-kg man who pushes a crate 5 m up along a ramp that makes an angle of 15º with the horizontal.(See
Figure 7.35.) He exerts a force of 400 N on the crate parallel to the ramp and moves at a constant speed. Be certain to include the work hedoes on the crate
and on his body to get up the ramp.(Notes: Assume that the man's effort starts at this point; don't worry about how the crate got to the pictured position. If you know the trigonometry, use it, but otherwise understand that the force exerted by the man parallel to his direction of motion up the 15 degree incline is about 25% of his weight.)
Figure 7.35
A man pushes a crate up a ramp.6.
How much work is done by the boy pulling his sister 30.0 m in a wagonas shown in
Figure 7.36? Assume no friction acts on the wagon.
Figure 7.36
The boy does work on the system of the wagon and the child when hepulls them as shown.
7.
A shopper pushes a grocery cart 20.0 m at constant speed on levelground, against a 35.0 N frictional force. He pushes in a direction
25.0ºbelow the horizontal. (a) What is the work done on the cart by friction? (b)
What is the work done on the cart by the gravitational force? (c) What is
the work done on the cart by the shopper? (d) Find the force the shopper
exerts, using energy considerations. (e) What is the total work done on
the cart?
8.
Suppose the ski patrol lowers a rescue sled and victim, having a totalmass of 80.0 kg, down a
60.0º slope at constant speed, as shown inFigure 7.37
. The frictional force is 7% of the normal force between the skier and the slope. The weight of the skier has components in the direction of the slope, and perpendicular to the direction of the slope, the former being about 87% of her weight and the latter 50%. The net force perpendicular to the slope is zero.(a) How much work is done by friction as the sled moves 25 m along the hill?
(b) How much work is done by the rope on the sled in this distance?
(c) What is the work done by the gravitational force on the sled?
(d) What is the total work done?
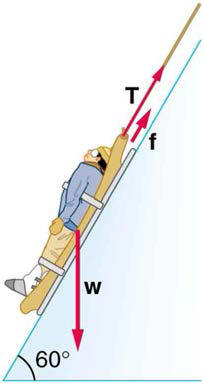
Figure 7.37
A rescue sled and victim are lowered down a steep slope.7.2 Kinetic Energy and the Work-Energy Theorem
9.
Compare the kinetic energy of a 20,000-kg truck moving at 110 km/hwith that of an 80.0-kg astronaut in orbit moving at 27,500 km/h.
10.
(a) How fast must a 3000-kg elephant move to have the same kineticenergy as a 65.0-kg sprinter running at 10.0 m/s? (b) Discuss how the
larger energies needed for the movement of larger animals would relate
to metabolic rates.
11.
Confirm the value given for the kinetic energy of an aircraft carrier inTable 7.1
. You will need to look up the definition of a nautical mile (1 knot= 1 nautical mile/h).
12.
(a) Calculate the force needed to bring a 950-kg car to rest from a speed of 90.0 km/h in a distance of 120 m (a fairly typical distance for anon-panic stop).
(b) Suppose instead the car hits a concrete abutment at full speed and is brought to a stop in 2.00 m. Calculate the force exerted on the car and compare it with the force found in part (a).
13.
A car’s bumper is designed to withstand a 4.0-km/h (1.1-m/s) collisionwith an immovable object without damage to the body of the car. The
bumper cushions the shock by absorbing the force over a distance.
Calculate the magnitude of the average force on a bumper that collapses
0.200 m while bringing a 900-kg car to rest from an initial speed of 1.1
m/s.
14.
Boxing gloves are padded to lessen the force of a blow. (a) Calculatethe force exerted by a boxing glove on an opponent’s face, if the glove
and face compress 7.50 cm during a blow in which the 7.00-kg arm and
glove are brought to rest from an initial speed of 10.0 m/s. (b) Calculate
the force exerted by an identical blow in the gory old days when no
gloves were used and the knuckles and face would compress only 2.00
cm. (c) Discuss the magnitude of the force with glove on. Does it seem
high enough to cause damage even though it is lower than the force with
no glove?
15.
Using energy considerations, calculate the average force a 60.0-kgsprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s
in a distance of 25.0 m, if he encounters a headwind that exerts an
average force of 30.0 N against him.
7.3 Gravitational Potential Energy
16.
A hydroelectric power facility (see Figure 7.38) converts the gravitational potential energy of water behind a dam to electric energy.(a) What is the gravitational potential energy relative to the generators of a lake of volume
100 km^3 ( mass = 10^14 kg) , given that thelake has an average height of 50 m above the generators?
(b) Compare this with the energy stored in a 10-megaton fusion bomb.
CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES 255

Figure 7.38
Hydroelectric facility (credit: Denis Belevich, Wikimedia Commons)17.
(a) How much gravitational potential energy (relative to the ground onwhich it is built) is stored in the Great Pyramid of Cheops, given that its
mass is about
7 × 109 kg and its center of mass is 36.5 m above thesurrounding ground? (b) How does this energy compare with the daily
food intake of a person?
18.
Suppose a 350-g kookaburra (a large kingfisher bird) picks up a 75-gsnake and raises it 2.5 m from the ground to a branch. (a) How much
work did the bird do on the snake? (b) How much work did it do to raise
its own center of mass to the branch?
19.
In Example 7.7, we found that the speed of a roller coaster that haddescended 20.0 m was only slightly greater when it had an initial speed
of 5.00 m/s than when it started from rest. This implies that
ΔPE >> KE
i . Confirm this statement by taking the ratio of ΔPE toKE
i . (Note that mass cancels.)20.
A 100-g toy car is propelled by a compressed spring that starts itmoving. The car follows the curved track in
Figure 7.39. Show that thefinal speed of the toy car is 0.687 m/s if its initial speed is 2.00 m/s and it
coasts up the frictionless slope, gaining 0.180 m in altitude.

Figure 7.39
A toy car moves up a sloped track. (credit: Leszek Leszczynski, Flickr)21.
In a downhill ski race, surprisingly, little advantage is gained by getting a running start. (This is because the initial kinetic energy is smallcompared with the gain in gravitational potential energy on even small hills.) To demonstrate this, find the final speed and the time taken for a
skier who skies 70.0 m along a
30º slope neglecting friction: (a) Starting from rest. (b) Starting with an initial speed of 2.50 m/s. (c) Does theanswer surprise you? Discuss why it is still advantageous to get a running start in very competitive events.
(Note: On a 30 degree slope the skier descends half a meter for every meter she moves forward, and the component of the gravitational force in the direction down the incline is half her weight.)
7.4 Conservative Forces and Potential Energy
22.
A 5.00×105-kg subway train is brought to a stop from a speed of0.500 m/s in 0.400 m by a large spring bumper at the end of its track.
What is the force constant
k of the spring?23.
A pogo stick has a spring with a force constant of 2.50×104 N/m ,which can be compressed 12.0 cm. To what maximum height can a child
jump on the stick using only the energy in the spring, if the child and stick
have a total mass of 40.0 kg? Explicitly show how you follow the steps in
the
Problem-Solving Strategies for Energy.7.5 Nonconservative Forces
24.
A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-mhighrise as shown in
Figure 7.40. Find her final speed at the top, giventhat the coefficient of friction between her skis and the snow is 0.0800.
(Hint: Find the distance traveled up the incline assuming a straight-line
path as shown in the figure.)
[The normal force between the incline and the skier is about 82% of her weight and the frictional force is 8% of that. It is recommended that you show how the figure for the normal force is obtained using trigonometry, if at this point you know how to do so.]
[Principles of Physics students can assume negligible friction]
Figure 7.40
The skier’s initial kinetic energy is partially used in coasting to the top of arise.
25.
(a) How high a hill can a car coast up (engine disengaged) if workdone by friction is negligible and its initial speed is 110 km/h? (b) If, in
actuality, a 750-kg car with an initial speed of 110 km/h is observed to
coast up a hill to a height 22.0 m above its starting point, how much
thermal energy was generated by friction? (c) What is the average force
of friction if the hill has a slope
2.5º above the horizontal?[The normal force on the car when on a 2.5 degree incline is 99.5% of its weight, which you should verify if at this point of the course you know how.]
[Principles of Physics students may omit part c]
7.6 Conservation of Energy
26.
Using values from Table 7.1, how many DNA molecules could bebroken by the energy carried by a single electron in the beam of an old-fashioned
TV tube? (These electrons were not dangerous in themselves,
but they did create dangerous x rays. Later model tube TVs had shielding
that absorbed x rays before they escaped and exposed viewers.)
27.
Using energy considerations and assuming negligible air resistance,show that a rock thrown from a bridge 20.0 m above water with an initial
speed of 15.0 m/s strikes the water with a speed of 24.8 m/s independent
of the direction thrown.
28.
If the energy in fusion bombs were used to supply the energy needsof the world, how many of the 9-megaton variety would be needed for a
year’s supply of energy (using data from
Table 7.1)? This is not as farfetchedas it may sound—there are thousands of nuclear bombs, and
their energy can be trapped in underground explosions and converted to
electricity, as natural geothermal energy is.
29.
(a) Use of hydrogen fusion to supply energy is a dream that may berealized in the next century. Fusion would be a relatively clean and
almost limitless supply of energy, as can be seen from
Table 7.1. Toillustrate this, calculate how many years the present energy needs of the
world could be supplied by one millionth of the oceans’ hydrogen fusion
energy. (b) How does this time compare with historically significant
events, such as the duration of stable economic systems?
7.7 Power
30.
The Crab Nebula (see Figure 7.41) pulsar is the remnant of asupernova that occurred in A.D. 1054. Using data from
Table 7.3,calculate the approximate factor by which the power output of this
astronomical object has declined since its explosion.
256 CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES

Figure 7.41
Crab Nebula (credit: ESO, via Wikimedia Commons)31.
Suppose a star 1000 times brighter than our Sun (that is, emitting1000 times the power) suddenly goes supernova. Using data from
Table7.3
: (a) By what factor does its power output increase? (b) How manytimes brighter than our entire Milky Way galaxy is the supernova? (c)
Based on your answers, discuss whether it should be possible to observe
supernovas in distant galaxies. Note that there are on the order of
1011observable galaxies, the average brightness of which is somewhat less
than our own galaxy.
32.
A person in good physical condition can put out 100 W of usefulpower for several hours at a stretch, perhaps by pedaling a mechanism
that drives an electric generator. Neglecting any problems of generator
efficiency and practical considerations such as resting time: (a) How
many people would it take to run a 4.00-kW electric clothes dryer? (b)
How many people would it take to replace a large electric power plant
that generates 800 MW?
33.
What is the cost of operating a 3.00-W electric clock for a year if thecost of electricity is $0.0900 per
kW ⋅ h ?34.
A large household air conditioner may consume 15.0 kW of power.What is the cost of operating this air conditioner 3.00 h per day for 30.0 d
if the cost of electricity is $0.110 per
kW ⋅ h ?35.
(a) What is the average power consumption in watts of an appliancethat uses
5.00 kW ⋅ h of energy per day? (b) How many joules ofenergy does this appliance consume in a year?
36.
(a) What is the average useful power output of a person who does6.00
×106 J of useful work in 8.00 h? (b) Working at this rate, how longwill it take this person to lift 2000 kg of bricks 1.50 m to a platform? (Work
done to lift his body can be omitted because it is not considered useful
output here.)
37.
A 500-kg dragster accelerates from rest to a final speed of 110 m/s in400 m (about a quarter of a mile) and encounters an average frictional
force of 1200 N. What is its average power output in watts and
horsepower if this takes 7.30 s?
38.
(a) How long will it take an 850-kg car with a useful power output of40.0 hp (1 hp = 746 W) to reach a speed of 15.0 m/s, neglecting friction?
(b) How long will this acceleration take if the car also climbs a 3.00-mhigh
hill in the process?
39.
(a) Find the useful power output of an elevator motor that lifts a2500-kg load a height of 35.0 m in 12.0 s, if it also increases the speed
from rest to 4.00 m/s. Note that the total mass of the counterbalanced
system is 10,000 kg—so that only 2500 kg is raised in height, but the full
10,000 kg is accelerated. (b) What does it cost, if electricity is $0.0900
per
kW ⋅ h ?40.
(a) What is the available energy content, in joules, of a battery thatoperates a 2.00-W electric clock for 18 months? (b) How long can a
battery that can supply
8.00×104 J run a pocket calculator thatconsumes energy at the rate of
1.00×10−3 W ?41.
(a) How long would it take a 1.50×105 -kg airplane with engines thatproduce 100 MW of power to reach a speed of 250 m/s and an altitude of
12.0 km if air resistance were negligible? (b) If it actually takes 900 s,
what is the power? (c) Given this power, what is the average force of air
resistance if the airplane takes 1200 s? (Hint: You must find the distance
the plane travels in 1200 s assuming constant acceleration.)
42.
Calculate the power output needed for a 950-kg car to climb a 2.00ºslope at a constant 30.0 m/s while encountering wind resistance and
friction totaling 600 N. Explicitly show how you follow the steps in the
Problem-Solving Strategies for Energy
.43.
(a) Calculate the power per square meter reaching Earth’s upperatmosphere from the Sun. (Take the power output of the Sun to be
4.00×10
26 W.) (b) Part of this is absorbed and reflected by theatmosphere, so that a maximum of
1.30 kW/m2 reaches Earth’ssurface. Calculate the area in
km2 of solar energy collectors needed toreplace an electric power plant that generates 750 MW if the collectors
convert an average of 2.00% of the maximum power into electricity. (This
small conversion efficiency is due to the devices themselves, and the fact
that the sun is directly overhead only briefly.) With the same
assumptions, what area would be needed to meet the United States’
energy needs
(1.05×1020 J)? Australia’s energy needs(5.4×10
18 J)? China’s energy needs (6.3×1019 J)? (These energyconsumption values are from 2006.)
7.8 Work, Energy, and Power in Humans
44.
(a) How long can you rapidly climb stairs (116/min) on the 93.0 kcal ofenergy in a 10.0-g pat of butter? (b) How many flights is this if each flight
has 16 stairs?
45.
(a) What is the power output in watts and horsepower of a 70.0-kgsprinter who accelerates from rest to 10.0 m/s in 3.00 s? (b) Considering
the amount of power generated, do you think a well-trained athlete could
do this repetitively for long periods of time?
46.
Calculate the power output in watts and horsepower of a shot-putterwho takes 1.20 s to accelerate the 7.27-kg shot from rest to 14.0 m/s,
while raising it 0.800 m. (Do not include the power produced to
accelerate his body.)

Figure 7.42
Shot putter at the Dornoch Highland Gathering in 2007. (credit: JohnHaslam, Flickr)
47.
(a) What is the efficiency of an out-of-condition professor who does2.10
×105 J of useful work while metabolizing 500 kcal of food energy?(b) How many food calories would a well-conditioned athlete metabolize
in doing the same work with an efficiency of 20%?
CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES 257
48.
Energy that is not utilized for work or heat transfer is converted to thechemical energy of body fat containing about 39 kJ/g. How many grams
of fat will you gain if you eat 10,000 kJ (about 2500 kcal) one day and do
nothing but sit relaxed for 16.0 h and sleep for the other 8.00 h? Use data
from
Table 7.5 for the energy consumption rates of these activities.49.
Using data from Table 7.5, calculate the daily energy needs of aperson who sleeps for 7.00 h, walks for 2.00 h, attends classes for 4.00
h, cycles for 2.00 h, sits relaxed for 3.00 h, and studies for 6.00 h.
(Studying consumes energy at the same rate as sitting in class.)
50.
What is the efficiency of a subject on a treadmill who puts out work atthe rate of 100 W while consuming oxygen at the rate of 2.00 L/min?
(Hint: See
Table 7.5.)51.
Shoveling snow can be extremely taxing because the arms havesuch a low efficiency in this activity. Suppose a person shoveling a
footpath metabolizes food at the rate of 800 W. (a) What is her useful
power output? (b) How long will it take her to lift 3000 kg of snow 1.20 m?
(This could be the amount of heavy snow on 20 m of footpath.) (c) How
much waste heat transfer in kilojoules will she generate in the process?
52.
Very large forces are produced in joints when a person jumps fromsome height to the ground. (a) Calculate the force produced if an 80.0-kg
person jumps from a 0.600–m-high ledge and lands stiffly, compressing
joint material 1.50 cm as a result. (Be certain to include the weight of the
person.) (b) In practice the knees bend almost involuntarily to help extend
the distance over which you stop. Calculate the force produced if the
stopping distance is 0.300 m. (c) Compare both forces with the weight of
the person.
53.
Jogging on hard surfaces with insufficiently padded shoes produceslarge forces in the feet and legs. (a) Calculate the force needed to stop
the downward motion of a jogger’s leg, if his leg has a mass of 13.0 kg, a
speed of 6.00 m/s, and stops in a distance of 1.50 cm. (Be certain to
include the weight of the 75.0-kg jogger’s body.) (b) Compare this force
with the weight of the jogger.
54.
(a) Calculate the energy in kJ used by a 55.0-kg woman who does 50deep knee bends in which her center of mass is lowered and raised
0.400 m. (She does work in both directions.) You may assume her
efficiency is 20%. (b) What is the average power consumption rate in
watts if she does this in 3.00 min?
55.
Kanellos Kanellopoulos flew 119 km from Crete to Santorini, Greece,on April 23, 1988, in the
Daedalus 88, an aircraft powered by a bicycletypedrive mechanism (see
Figure 7.43). His useful power output for the234-min trip was about 350 W. Using the efficiency for cycling from
Table7.2
, calculate the food energy in kilojoules he metabolized during theflight.
Figure 7.43
The Daedalus 88 in flight. (credit: NASA photo by Beasley)56.
The swimmer shown in Figure 7.44 exerts an average horizontalbackward force of 80.0 N with his arm during each 1.80 m long stroke. (a)
What is his work output in each stroke? (b) Calculate the power output of
his arms if he does 120 strokes per minute.
 Figure 7.44
Figure 7.44
57.
Mountain climbers carry bottled oxygen when at very high altitudes.(a) Assuming that a mountain climber uses oxygen at twice the rate for
climbing 116 stairs per minute (because of low air temperature and
winds), calculate how many liters of oxygen a climber would need for
10.0 h of climbing. (These are liters at sea level.) Note that only 40% of
the inhaled oxygen is utilized; the rest is exhaled. (b) How much useful
work does the climber do if he and his equipment have a mass of 90.0 kg
and he gains 1000 m of altitude? (c) What is his efficiency for the 10.0-h
climb?
58.
The awe-inspiring Great Pyramid of Cheops was built more than4500 years ago. Its square base, originally 230 m on a side, covered 13.1
acres, and it was 146 m high, with a mass of about
7×109 kg . (Thepyramid’s dimensions are slightly different today due to quarrying and
some sagging.) Historians estimate that 20,000 workers spent 20 years
to construct it, working 12-hour days, 330 days per year. (a) Calculate the
gravitational potential energy stored in the pyramid, given its center of
mass is at one-fourth its height. (b) Only a fraction of the workers lifted
blocks; most were involved in support services such as building ramps
(see
Figure 7.45), bringing food and water, and hauling blocks to the site.Calculate the efficiency of the workers who did the lifting, assuming there
were 1000 of them and they consumed food energy at the rate of 300
kcal/h. What does your answer imply about how much of their work went
into block-lifting, versus how much work went into friction and lifting and
lowering their own bodies? (c) Calculate the mass of food that had to be
supplied each day, assuming that the average worker required 3600 kcal
per day and that their diet was 5% protein, 60% carbohydrate, and 35%
fat. (These proportions neglect the mass of bulk and nondigestible
materials consumed.)
Figure 7.45
Ancient pyramids were probably constructed using ramps as simplemachines. (credit: Franck Monnier, Wikimedia Commons)
59.
(a) How long can you play tennis on the 800 kJ (about 200 kcal) ofenergy in a candy bar? (b) Does this seem like a long time? Discuss why
exercise is necessary but may not be sufficient to cause a person to lose
weight.
7.9 World Energy Use
60. Integrated Concepts
(a) Calculate the force the woman in
Figure 7.46 exerts to do a push-upat constant speed, taking all data to be known to three digits. (b) How
much work does she do if her center of mass rises 0.240 m? (c) What is
her useful power output if she does 25 push-ups in 1 min? (Should work
258 CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES
done lowering her body be included? See the discussion of useful work in
Work, Energy, and Power in Humans
.
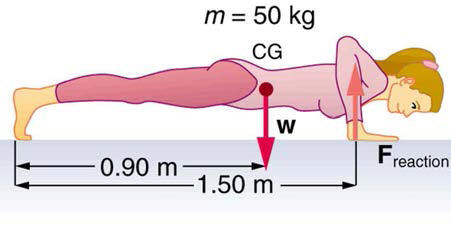
Figure 7.46
Forces involved in doing push-ups. The woman’s weight acts as a forceexerted downward on her center of gravity (CG).
61. Integrated Concepts
A 75.0-kg cross-country skier is climbing a
3.0º slope at a constantspeed of 2.00 m/s and encounters air resistance of 25.0 N. Find his
power output for work done against the gravitational force and air
resistance. (b) What average force does he exert backward on the snow
to accomplish this? (c) If he continues to exert this force and to
experience the same air resistance when he reaches a level area, how
long will it take him to reach a velocity of 10.0 m/s?
62. Integrated Concepts
The 70.0-kg swimmer in
Figure 7.44 starts a race with an initial velocityof 1.25 m/s and exerts an average force of 80.0 N backward with his
arms during each 1.80 m long stroke. (a) What is his initial acceleration if
water resistance is 45.0 N? (b) What is the subsequent average
resistance force from the water during the 5.00 s it takes him to reach his
top velocity of 2.50 m/s? (c) Discuss whether water resistance seems to
increase linearly with velocity.
63. Integrated Concepts
A toy gun uses a spring with a force constant of 300 N/m to propel a
10.0-g steel ball. If the spring is compressed 7.00 cm and friction is
negligible: (a) How much force is needed to compress the spring? (b) To
what maximum height can the ball be shot? (c) At what angles above the
horizontal may a child aim to hit a target 3.00 m away at the same height
as the gun? (d) What is the gun’s maximum range on level ground?
64. Integrated Concepts
(a) What force must be supplied by an elevator cable to produce an
acceleration of
0.800 m/s2 against a 200-N frictional force, if the massof the loaded elevator is 1500 kg? (b) How much work is done by the
cable in lifting the elevator 20.0 m? (c) What is the final speed of the
elevator if it starts from rest? (d) How much work went into thermal
energy?
65. Unreasonable Results
A car advertisement claims that its 900-kg car accelerated from rest to
30.0 m/s and drove 100 km, gaining 3.00 km in altitude, on 1.0 gal of
gasoline. The average force of friction including air resistance was 700 N.
Assume all values are known to three significant
gases?
CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 283
Problems & Exercises
8.1 Linear Momentum and Force
1.
(a) Calculate the momentum of a 2000-kg elephant charging a hunterat a speed of
7.50 m/s . (b) Compare the elephant’s momentum with themomentum of a 0.0400-kg tranquilizer dart fired at a speed of
600 m/s .(c) What is the momentum of the 90.0-kg hunter running at
7.40 m/safter missing the elephant?
2.
(a) What is the mass of a large ship that has a momentum of1.60×10
9 kg · m/s , when the ship is moving at a speed of48.0 km/h?
(b) Compare the ship’s momentum to the momentum of a1100-kg artillery shell fired at a speed of
1200 m/s .3.
(a) At what speed would a 2.00×104-kg airplane have to fly to havea momentum of
1.60×109 kg · m/s (the same as the ship’s momentumin the problem above)? (b) What is the plane’s momentum when it is
taking off at a speed of
60.0 m/s ? (c) If the ship is an aircraft carrier thatlaunches these airplanes with a catapult, discuss the implications of your
answer to (b) as it relates to recoil effects of the catapult on the ship.
4.
(a) What is the momentum of a garbage truck that is 1.20×104 kgand is moving at
10.0 m/s ? (b) At what speed would an 8.00-kg trashcan have the same momentum as the truck?
5.
A runaway train car that has a mass of 15,000 kg travels at a speed of5.4 m/s
down a track. Compute the time required for a force of 1500 Nto bring the car to rest.
6.
The mass of Earth is 5.972×1024 kg and its orbital radius is anaverage of
1.496×1011 m . Calculate its linear momentum.8.2 Impulse
7.
A bullet is accelerated down the barrel of a gun by hot gases producedin the combustion of gun powder. What is the average force exerted on a
0.0300-kg bullet to accelerate it to a speed of 600 m/s in a time of 2.00
ms (milliseconds)?
8. Professional Application
A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate
the force the seat belt exerts on a passenger in the car to bring him to a
halt. The mass of the passenger is 70 kg.
9.
A person slaps her leg with her hand, bringing her hand to rest in 2.50milliseconds from an initial speed of 4.00 m/s. (a) What is the average
force exerted on the leg, taking the effective mass of the hand and
forearm to be 1.50 kg? (b) Would the force be any different if the woman
clapped her hands together at the same speed and brought them to rest
in the same time? Explain why or why not.
10. Professional Application
A professional boxer hits his opponent with a 1000-N horizontal blow that
lasts for 0.150 s. (a) Calculate the impulse imparted by this blow. (b)
What is the opponent’s final velocity, if his mass is 105 kg and he is
motionless in midair when struck near his center of mass? (c) Calculate
the recoil velocity of the opponent’s 10.0-kg head if hit in this manner,
assuming the head does not initially transfer significant momentum to the
boxer’s body. (d) Discuss the implications of your answers for parts (b)
and (c).
11. Professional Application
Suppose a child drives a bumper car head on into the side rail, which
exerts a force of 4000 N on the car for 0.200 s. (a) What impulse is
imparted by this force? (b) Find the final velocity of the bumper car if its
initial velocity was 2.80 m/s and the car plus driver have a mass of 200
kg. You may neglect friction between the car and floor.
12. Professional Application
One hazard of space travel is debris left by previous missions. There are
several thousand objects orbiting Earth that are large enough to be
detected by radar, but there are far greater numbers of very small
objects, such as flakes of paint. Calculate the force exerted by a
0.100-mg chip of paint that strikes a spacecraft window at a relative
speed of
4.00×103 m/s , given the collision lasts 6.00×10 – 8 s .13. Professional Application
A 75.0-kg person is riding in a car moving at 20.0 m/s when the car runs
into a bridge abutment. (a) Calculate the average force on the person if
he is stopped by a padded dashboard that compresses an average of
1.00 cm. (b) Calculate the average force on the person if he is stopped
by an air bag that compresses an average of 15.0 cm.
14. Professional Application
Military rifles have a mechanism for reducing the recoil forces of the gun
on the person firing it. An internal part recoils over a relatively large
distance and is stopped by damping mechanisms in the gun. The larger
distance reduces the average force needed to stop the internal part. (a)
Calculate the recoil velocity of a 1.00-kg plunger that directly interacts
with a 0.0200-kg bullet fired at 600 m/s from the gun. (b) If this part is
stopped over a distance of 20.0 cm, what average force is exerted upon it
by the gun? (c) Compare this to the force exerted on the gun if the bullet
is accelerated to its velocity in 10.0 ms (milliseconds).
15.
A cruise ship with a mass of 1.00×107 kg strikes a pier at a speedof 0.750 m/s. It comes to rest 6.00 m later, damaging the ship, the pier,
and the tugboat captain’s finances. Calculate the average force exerted
on the pier using the concept of impulse. (Hint: First calculate the time it
took to bring the ship to rest.)
16.
Calculate the final speed of a 110-kg rugby player who is initiallyrunning at 8.00 m/s but collides head-on with a padded goalpost and
experiences a backward force of
1.76×104 N for 5.50×10–2 s .17.
Water from a fire hose is directed horizontally against a wall at a rateof 50.0 kg/s and a speed of 42.0 m/s. Calculate the force exerted on the
wall, assuming the water’s horizontal momentum is reduced to zero.
18.
A 0.450-kg hammer is moving horizontally at 7.00 m/s when it strikesa nail and comes to rest after driving the nail 1.00 cm into a board. (a)
Calculate the duration of the impact. (b) What was the average force
exerted on the nail?
19.
Starting with the definitions of momentum and kinetic energy, derivean equation for the kinetic energy of a particle expressed as a function of
its momentum
20.
A ball with an initial velocity of 10 m/s moves at an angle 60º abovethe
+x -direction. The ball hits a vertical wall and bounces off so that it ismoving
60º above the −x -direction with the same speed. What is theimpulse delivered by the wall?
21.
When serving a tennis ball, a player hits the ball when its velocity iszero (at the highest point of a vertical toss). The racquet exerts a force of
540 N on the ball for 5.00 ms, giving it a final velocity of 45.0 m/s. Using
these data, find the mass of the ball.
22.
A punter drops a ball from rest vertically 1 meter down onto his foot.The ball leaves the foot with a speed of 18 m/s at an angle
55º abovethe horizontal. What is the impulse delivered by the foot (magnitude and
direction)?
8.3 Conservation of Momentum
23. Professional Application
Train cars are coupled together by being bumped into one another.
Suppose two loaded train cars are moving toward one another, the first
having a mass of 150,000 kg and a velocity of 0.300 m/s, and the second
having a mass of 110,000 kg and a velocity of
−0.120 m/s . (The minusindicates direction of motion.) What is their final velocity?
24.
Suppose a clay model of a koala bear has a mass of 0.200 kg andslides on ice at a speed of 0.750 m/s. It runs into another clay model,
284 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
which is initially motionless and has a mass of 0.350 kg. Both being soft
clay, they naturally stick together. What is their final velocity?
25. Professional Application
Consider the following question:
A car moving at 10 m/s crashes into atree and stops in 0.26 s. Calculate the force the seatbelt exerts on a
passenger in the car to bring him to a halt. The mass of the passenger is
70 kg.
Would the answer to this question be different if the car with the70-kg passenger had collided with a car that has a mass equal to and is
traveling in the opposite direction and at the same speed? Explain your
answer.
26.
What is the velocity of a 900-kg car initially moving at 30.0 m/s, justafter it hits a 150-kg deer initially running at 12.0 m/s in the same
direction? Assume the deer remains on the car.
27.
A 1.80-kg falcon catches a 0.650-kg dove from behind in midair. Whatis their velocity after impact if the falcon’s velocity is initially 28.0 m/s and
the dove’s velocity is 7.00 m/s in the same direction?
8.4 Elastic Collisions in One Dimension
28.
Two identical objects (such as billiard balls) have a one-dimensionalcollision in which one is initially motionless. After the collision, the moving
object is stationary and the other moves with the same speed as the
other originally had. Show that both momentum and kinetic energy are
conserved.
29. Professional Application
Two manned satellites approach one another at a relative speed of 0.250
m/s, intending to dock. The first has a mass of
4.00×103 kg , and thesecond a mass of
7.50×103 kg . If the two satellites collide elasticallyrather than dock, what is their final relative velocity?
30.
A 70.0-kg ice hockey goalie, originally at rest, catches a 0.150-kghockey puck slapped at him at a velocity of 35.0 m/s. Suppose the goalie
and the ice puck have an elastic collision and the puck is reflected back
in the direction from which it came. What would their final velocities be in
this case?
8.5 Inelastic Collisions in One Dimension
31.
A 0.240-kg billiard ball that is moving at 3.00 m/s strikes the bumperof a pool table and bounces straight back at 2.40 m/s (80% of its original
speed). The collision lasts 0.0150 s. (a) Calculate the average force
exerted on the ball by the bumper. (b) How much kinetic energy in joules
is lost during the collision? (c) What percent of the original energy is left?
32.
During an ice show, a 60.0-kg skater leaps into the air and is caughtby an initially stationary 75.0-kg skater. (a) What is their final velocity
assuming negligible friction and that the 60.0-kg skater’s original
horizontal velocity is 4.00 m/s? (b) How much kinetic energy is lost?
33. Professional Application
Using mass and speed data from
Example 8.1 and assuming that thefootball player catches the ball with his feet off the ground with both of
them moving horizontally, calculate: (a) the final velocity if the ball and
player are going in the same direction and (b) the loss of kinetic energy in
this case. (c) Repeat parts (a) and (b) for the situation in which the ball
and the player are going in opposite directions. Might the loss of kinetic
energy be related to how much it hurts to catch the pass?
34.
A battleship that is 6.00×107 kg and is originally at rest fires a1100-kg artillery shell horizontally with a velocity of 575 m/s. (a) If the
shell is fired straight aft (toward the rear of the ship), there will be
negligible friction opposing the ship’s recoil. Calculate its recoil velocity.
(b) Calculate the increase in internal kinetic energy (that is, for the ship
and the shell). This energy is less than the energy released by the gun
powder—ignificant heat transfer occurs.
35. Professional Application
Two manned satellites approaching one another, at a relative speed of
0.250 m/s, intending to dock. The first has a mass of
4.00×103 kg , andthe second a mass of
7.50×103 kg . (a) Calculate the final velocity(after docking) by using the frame of reference in which the first satellite
was originally at rest. (b) What is the loss of kinetic energy in this inelastic
collision? (c) Repeat both parts by using the frame of reference in which
the second satellite was originally at rest. Explain why the change in
velocity is different in the two frames, whereas the change in kinetic
energy is the same in both.
36. Professional Application
A 30,000-kg freight car is coasting at 0.850 m/s with negligible friction
under a hopper that dumps 110,000 kg of scrap metal into it. (a) What is
the final velocity of the loaded freight car? (b) How much kinetic energy is
lost?
37. Professional Application
Space probes may be separated from their launchers by exploding bolts.
(They bolt away from one another.) Suppose a 4800-kg satellite uses this
method to separate from the 1500-kg remains of its launcher, and that
5000 J of kinetic energy is supplied to the two parts. What are their
subsequent velocities using the frame of reference in which they were at
rest before separation?
38.
A 0.0250-kg bullet is accelerated from rest to a speed of 550 m/s in a3.00-kg rifle. The pain of the rifle’s kick is much worse if you hold the gun
loosely a few centimeters from your shoulder rather than holding it tightly
against your shoulder. (a) Calculate the recoil velocity of the rifle if it is
held loosely away from the shoulder. (b) How much kinetic energy does
the rifle gain? (c) What is the recoil velocity if the rifle is held tightly
against the shoulder, making the effective mass 28.0 kg? (d) How much
kinetic energy is transferred to the rifle-shoulder combination? The pain is
related to the amount of kinetic energy, which is significantly less in this
latter situation. (e) Calculate the momentum of a 110-kg football player
running at 8.00 m/s. Compare the player’s momentum with the
momentum of a hard-thrown 0.410-kg football that has a speed of 25.0
m/s. Discuss its relationship to this problem.
39. Professional Application
One of the waste products of a nuclear reactor is plutonium-239
⎛⎝
239
Pu⎞⎠. This nucleus is radioactive and decays by splitting into a
helium-4 nucleus and a uranium-235 nucleus
⎛⎝4
He + 235 U⎞⎠, the latter
of which is also radioactive and will itself decay some time later. The
energy emitted in the plutonium decay is
8.40×10 – 13 J and is entirelyconverted to kinetic energy of the helium and uranium nuclei. The mass
of the helium nucleus is
6.68×10 – 27 kg , while that of the uranium is3.92×10
– 25 kg (note that the ratio of the masses is 4 to 235). (a)Calculate the velocities of the two nuclei, assuming the plutonium
nucleus is originally at rest. (b) How much kinetic energy does each
nucleus carry away? Note that the data given here are accurate to three
digits only.
40. Professional Application
The Moon’s craters are remnants of meteorite collisions. Suppose a fairly
large asteroid that has a mass of
5.00×1012 kg (about a kilometeracross) strikes the Moon at a speed of 15.0 km/s. (a) At what speed does
the Moon recoil after the perfectly inelastic collision (the mass of the
Moon is
7.36×1022 kg ) ? (b) How much kinetic energy is lost in thecollision? Such an event may have been observed by medieval English
monks who reported observing a red glow and subsequent haze about
the Moon. (c) In October 2009, NASA crashed a rocket into the Moon,
and analyzed the plume produced by the impact. (Significant amounts of
water were detected.) Answer part (a) and (b) for this real-life experiment.
The mass of the rocket was 2000 kg and its speed upon impact was
9000 km/h. How does the plume produced alter these results?
41. Professional Application
Two football players collide head-on in midair while trying to catch a
thrown football. The first player is 95.0 kg and has an initial velocity of
CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 285
6.00 m/s, while the second player is 115 kg and has an initial velocity of
–3.50 m/s. What is their velocity just after impact if they cling together?
42.
What is the speed of a garbage truck that is 1.20×104 kg and isinitially moving at 25.0 m/s just after it hits and adheres to a trash can
that is 80.0 kg and is initially at rest?
43.
During a circus act, an elderly performer thrills the crowd by catchinga cannon ball shot at him. The cannon ball has a mass of 10.0 kg and the
horizontal component of its velocity is 8.00 m/s when the 65.0-kg
performer catches it. If the performer is on nearly frictionless roller
skates, what is his recoil velocity?
44.
(a) During an ice skating performance, an initially motionless 80.0-kgclown throws a fake barbell away. The clown’s ice skates allow her to
recoil frictionlessly. If the clown recoils with a velocity of 0.500 m/s and
the barbell is thrown with a velocity of 10.0 m/s, what is the mass of the
barbell? (b) How much kinetic energy is gained by this maneuver? (c)
Where does the kinetic energy come from?
8.6 Collisions of Point Masses in Two Dimensions
45.
Two identical pucks collide on an air hockey table. One puck wasoriginally at rest. (a) If the incoming puck has a speed of 6.00 m/s and
scatters to an angle of
30.0º ,what is the velocity (magnitude anddirection) of the second puck? (You may use the result that
θ
1 − θ2 = 90º for elastic collisions of objects that have identicalmasses.) (b) Confirm that the collision is elastic.
46.
Confirm that the results of the example Example 8.7 do conservemomentum in both the
x - and y -directions.47.
A 3000-kg cannon is mounted so that it can recoil only in thehorizontal direction. (a) Calculate its recoil velocity when it fires a 15.0-kg
shell at 480 m/s at an angle of
20.0º above the horizontal. (b) What isthe kinetic energy of the cannon? This energy is dissipated as heat
transfer in shock absorbers that stop its recoil. (c) What happens to the
vertical component of momentum that is imparted to the cannon when it
is fired?
48. Professional Application
A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg
bowling pin, which is scattered at an angle of
85.0º to the initial directionof the bowling ball and with a speed of 15.0 m/s. (a) Calculate the final
velocity (magnitude and direction) of the bowling ball. (b) Is the collision
elastic? (c) Linear kinetic energy is greater after the collision. Discuss
how spin on the ball might be converted to linear kinetic energy in the
collision.
49. Professional Application
Ernest Rutherford (the first New Zealander to be awarded the Nobel
Prize in Chemistry) demonstrated that nuclei were very small and dense
by scattering helium-4 nuclei
⎛⎝4
He⎞⎠from gold-197 nuclei
⎛⎝197 Au⎞⎠.
The energy of the incoming helium nucleus was
8.00×10−13 J , and themasses of the helium and gold nuclei were
6.68×10−27 kg and3.29×10
−25 kg , respectively (note that their mass ratio is 4 to 197). (a)If a helium nucleus scatters to an angle of
120º during an elasticcollision with a gold nucleus, calculate the helium nucleus’s final speed
and the final velocity (magnitude and direction) of the gold nucleus. (b)
What is the final kinetic energy of the helium nucleus?
50. Professional Application
Two cars collide at an icy intersection and stick together afterward. The
first car has a mass of 1200 kg and is approaching at
8.00 m/s duesouth. The second car has a mass of 850 kg and is approaching at
17.0 m/s
due west. (a) Calculate the final velocity (magnitude anddirection) of the cars. (b) How much kinetic energy is lost in the collision?
(This energy goes into deformation of the cars.) Note that because both
cars have an initial velocity, you cannot use the equations for
conservation of momentum along the
x -axis and y -axis; instead, youmust look for other simplifying aspects.
51.
Starting with equations m1 v1 = m1v′1 cos θ1 + m2v′2 cos θ2and
0 = m1v′1 sin θ1 + m2v′2 sin θ2 for conservation of momentumin the
x - and y -directions and assuming that one object is originallystationary, prove that for an elastic collision of two objects of equal
masses,
12mv
12
=12mv
′12
+12mv
′22
+mv′1v′2 cos⎛ ⎝θ1 − θ2⎞⎠
as discussed in the text.
52. Integrated Concepts
A 90.0-kg ice hockey player hits a 0.150-kg puck, giving the puck a
velocity of 45.0 m/s. If both are initially at rest and if the ice is frictionless,
how far does the player recoil in the time it takes the puck to reach the
goal 15.0 m away?
8.7 Introduction to Rocket Propulsion
53. Professional Application
Antiballistic missiles (ABMs) are designed to have very large
accelerations so that they may intercept fast-moving incoming missiles in
the short time available. What is the takeoff acceleration of a 10,000-kg
ABM that expels 196 kg of gas per second at an exhaust velocity of
2.50×10
3 m/s?54. Professional Application
What is the acceleration of a 5000-kg rocket taking off from the Moon,
where the acceleration due to gravity is only
1.6 m/s2 , if the rocketexpels 8.00 kg of gas per second at an exhaust velocity of
2.20×10
3 m/s?55. Professional Application
Calculate the increase in velocity of a 4000-kg space probe that expels
3500 kg of its mass at an exhaust velocity of
2.00×103 m/s . You mayassume the gravitational force is negligible at the probe’s location.
56. Professional Application
Ion-propulsion rockets have been proposed for use in space. They
employ atomic ionization techniques and nuclear energy sources to
produce extremely high exhaust velocities, perhaps as great as
8.00×10
6 m/s . These techniques allow a much more favorablepayload-to-fuel ratio. To illustrate this fact: (a) Calculate the increase in
velocity of a 20,000-kg space probe that expels only 40.0-kg of its mass
at the given exhaust velocity. (b) These engines are usually designed to
produce a very small thrust for a very long time—the type of engine that
might be useful on a trip to the outer planets, for example. Calculate the
acceleration of such an engine if it expels
4.50×10−6 kg/s at the givenvelocity, assuming the acceleration due to gravity is negligible.
57.
Derive the equation for the vertical acceleration of a rocket.58. Professional Application
(a) Calculate the maximum rate at which a rocket can expel gases if its
acceleration cannot exceed seven times that of gravity. The mass of the
rocket just as it runs out of fuel is 75,000-kg, and its exhaust velocity is
2.40×10
3 m/s . Assume that the acceleration of gravity is the same ason Earth’s surface
⎛⎝9.80 m/s
2⎞⎠. (b) Why might it be necessary to limit
the acceleration of a rocket?
59.
Given the following data for a fire extinguisher-toy wagon rocketexperiment, calculate the average exhaust velocity of the gases expelled
from the extinguisher. Starting from rest, the final velocity is 10.0 m/s.
The total mass is initially 75.0 kg and is 70.0 kg after the extinguisher is
fired.
286 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
60.
How much of a single-stage rocket that is 100,000 kg can be anythingbut fuel if the rocket is to have a final speed of
8.00 km/s , given that itexpels gases at an exhaust velocity of
2.20×103 m/s?61. Professional Application
(a) A 5.00-kg squid initially at rest ejects 0.250-kg of fluid with a velocity
of 10.0 m/s. What is the recoil velocity of the squid if the ejection is done
in 0.100 s and there is a 5.00-N frictional force opposing the squid’s
movement. (b) How much energy is lost to work done against friction?
62. Unreasonable Results
Squids have been reported to jump from the ocean and travel
30.0 m(measured horizontally) before re-entering the water. (a) Calculate the
initial speed of the squid if it leaves the water at an angle of
20.0º ,assuming negligible lift from the air and negligible air resistance. (b) The
squid propels itself by squirting water. What fraction of its mass would it
have to eject in order to achieve the speed found in the previous part?
The water is ejected at
12.0 m/s ; gravitational force and friction areneglected. (c) What is unreasonable about the results? (d) Which
premise is unreasonable, or which premises are inconsistent?
63. Professional Application
Consider an astronaut in deep space cut free from her space ship and
needing to get back to it. The astronaut has a few packages that she can
throw away to move herself toward the ship. Construct a problem in
which you calculate the time it takes her to get back by throwing all the
packages at one time compared to throwing them one at a time. Among
the things to be considered are the masses involved, the force she can
exert on the packages through some distance, and the distance to the
ship.
64.
Consider an artillery projectile striking armor plating. Construct aproblem in which you find the force exerted by the projectile on the plate.
Among the things to be considered are the mass and speed of the
projectile and the distance over which its speed is reduced. Your
instructor may also wish for you to consider the relative merits of
depleted uranium
9.2 The Second Condition for Equilibrium
1.
(a) When opening a door, you push on it perpendicularly with a force of55.0 N at a distance of 0.850m from the hinges. What torque are you
exerting relative to the hinges? (b) Does it matter if you push at the same
height as the hinges?
2.
When tightening a bolt, you push perpendicularly on a wrench with aforce of 165 N at a distance of 0.140 m from the center of the bolt. (a)
How much torque are you exerting in newton × meters (relative to the
center of the bolt)? (b) Convert this torque to footpounds.
3.
Two children push on opposite sides of a door during play. Both pushhorizontally and perpendicular to the door. One child pushes with a force
of 17.5 N at a distance of 0.600 m from the hinges, and the second child
pushes at a distance of 0.450 m. What force must the second child exert
to keep the door from moving? Assume friction is negligible.
4.
Use the second condition for equilibrium (net τ = 0) to calculate Fpin
Example 9.1, employing any data given or solved for in part (a) of theexample.
5.
Repeat the seesaw problem in Example 9.1 with the center of mass ofthe seesaw 0.160 m to the left of the pivot (on the side of the lighter child)
and assuming a mass of 12.0 kg for the seesaw. The other data given in
the example remain unchanged. Explicitly show how you follow the steps
in the Problem-Solving Strategy for static equilibrium.
9.3 Stability
6.
Suppose a horse leans against a wall as in Figure 9.31. Calculate theforce exerted on the wall assuming that force is horizontal while using the
data in the schematic representation of the situation. Note that the force
exerted on the wall is equal and opposite to the force exerted on the
horse, keeping it in equilibrium. The total mass of the horse and rider is
500 kg. Take the data to be accurate to three digits.
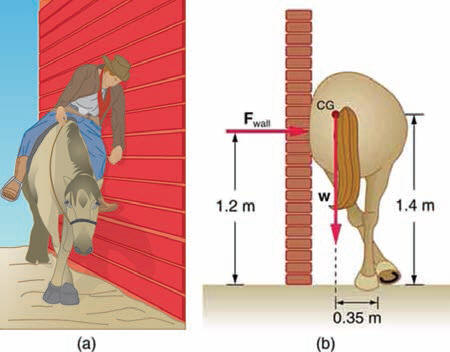 Figure 9.31
Figure 9.31
7.
Two children of mass 20 kg and 30 kg sit balanced on a seesaw withthe pivot point located at the center of the seesaw. If the children are
separated by a distance of 3 m, at what distance from the pivot point is
the small child sitting in order to maintain the balance?
8.
(a) Calculate the magnitude and direction of the force on each foot ofthe horse in
Figure 9.31 (two are on the ground), assuming the center ofmass of the horse is midway between the feet. The total mass of the
horse and rider is 500kg. (b) What is the minimum coefficient of friction
between the hooves and ground? Note that the force exerted by the wall
is horizontal.
9.
A person carries a plank of wood 2 m long with one hand pushingdown on it at one end with a force
F1 and the other hand holding it up at50 cm from the end of the plank with force
F2 . If the plank has a massof 20 kg and its center of gravity is at the middle of the plank, what are
the forces
F1 and F2 ?10.
A 17.0-m-high and 11.0-m-long wall under construction and itsbracing are shown in
Figure 9.32. The wall is in stable equilibriumwithout the bracing but can pivot at its base. Calculate the force exerted
by each of the 10 braces if a strong wind exerts a horizontal force of 650
N on each square meter of the wall. Assume that the net force from the
wind acts at a height halfway up the wall and that all braces exert equal
forces parallel to their lengths. Neglect the thickness of the wall.
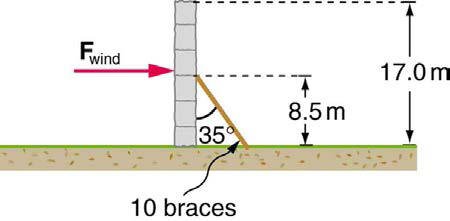 Figure 9.32
Figure 9.32
11.
(a) What force must be exerted by the wind to support a 2.50-kgchicken in the position shown in
Figure 9.33? (b) What is the ratio of thisforce to the chicken’s weight? (c) Does this support the contention that
the chicken has a relatively stable construction?
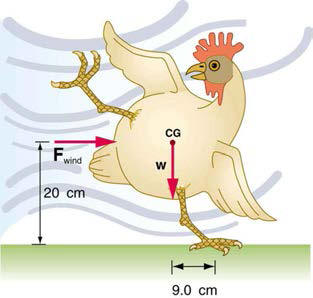
Figure 9.33
12.
Suppose the weight of the drawbridge in Figure 9.34 is supportedentirely by its hinges and the opposite shore, so that its cables are slack.
(a) What fraction of the weight is supported by the opposite shore if the
point of support is directly beneath the cable attachments? (b) What is
the direction and magnitude of the force the hinges exert on the bridge
under these circumstances? The mass of the bridge is 2500 kg.
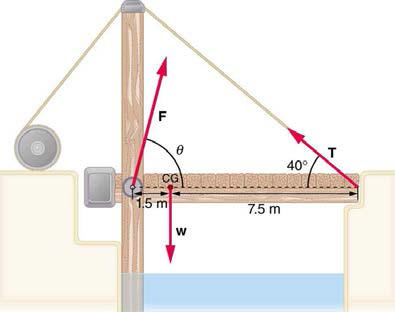
Figure 9.34
A small drawbridge, showing the forces on the hinges ( F ), its weight (w
), and the tension in its wires ( T ).13.
Suppose a 900-kg car is on the bridge in Figure 9.34 with its centerof mass halfway between the hinges and the cable attachments. (The
bridge is supported by the cables and hinges only.) (a) Find the force in
the cables. (b) Find the direction and magnitude of the force exerted by
the hinges on the bridge.
14.
A sandwich board advertising sign is constructed as shown in Figure9.35
. The sign’s mass is 8.00 kg. (a) Calculate the tension in the chain312 CHAPTER 9 | STATICS AND TORQUE
assuming no friction between the legs and the sidewalk. (b) What force is
exerted by each side on the hinge?
Figure 9.35
A sandwich board advertising sign demonstrates tension.15.
(a) What minimum coefficient of friction is needed between the legsand the ground to keep the sign in
Figure 9.35 in the position shown ifthe chain breaks? (b) What force is exerted by each side on the hinge?
16.
A gymnast is attempting to perform splits. From the information givenin
Figure 9.36, calculate the magnitude and direction of the force exertedon each foot by the floor.
Figure 9.36
A gymnast performs full split. The center of gravity and the variousdistances from it are shown.
9.4 Applications of Statics, Including Problem-Solving
Strategies
17.
To get up on the roof, a person (mass 70.0 kg) places a 6.00-maluminum ladder (mass 10.0 kg) against the house on a concrete pad
with the base of the ladder 2.00 m from the house. The ladder rests
against a plastic rain gutter, which we can assume to be frictionless. The
center of mass of the ladder is 2 m from the bottom. The person is
standing 3 m from the bottom. What are the magnitudes of the forces on
the ladder at the top and bottom?
18.
In Figure 9.21, the cg of the pole held by the pole vaulter is 2.00 mfrom the left hand, and the hands are 0.700 m apart. Calculate the force
exerted by (a) his right hand and (b) his left hand. (c) If each hand
supports half the weight of the pole in
Figure 9.19, show that the secondcondition for equilibrium
(net τ = 0) is satisfied for a pivot other thanthe one located at the center of gravity of the pole. Explicitly show how
you follow the steps in the Problem-Solving Strategy for static equilibrium
described above.
9.5 Simple Machines
19.
What is the mechanical advantage of a nail puller—similar to the oneshown in
Figure 9.23 —where you exert a force 45 cm from the pivotand the nail is
1.8 cm on the other side? What minimum force must youexert to apply a force of
1250 N to the nail?20.
Suppose you needed to raise a 250-kg mower a distance of 6.0 cmabove the ground to change a tire. If you had a 2.0-m long lever, where
would you place the fulcrum if your force was limited to 300 N?
21.
a) What is the mechanical advantage of a wheelbarrow, such as theone in
Figure 9.24, if the center of gravity of the wheelbarrow and its loadhas a perpendicular lever arm of 5.50 cm, while the hands have a
perpendicular lever arm of 1.02 m? (b) What upward force should you
exert to support the wheelbarrow and its load if their combined mass is
55.0 kg? (c) What force does the wheel exert on the ground?
22.
A typical car has an axle with 1.10 cm radius driving a tire with aradius of
27.5 cm . What is its mechanical advantage assuming the verysimplified model in
Figure 9.25(b)?23.
What force does the nail puller in Exercise 9.19 exert on thesupporting surface? The nail puller has a mass of 2.10 kg.
24.
If you used an ideal pulley of the type shown in Figure 9.26(a) tosupport a car engine of mass
115 kg , (a) What would be the tension inthe rope? (b) What force must the ceiling supply, assuming you pull
straight down on the rope? Neglect the pulley system’s mass.
25.
Repeat Exercise 9.24 for the pulley shown in Figure 9.26(c),assuming you pull straight up on the rope. The pulley system’s mass is
7.00 kg
.9.6 Forces and Torques in Muscles and Joints
26.
Verify that the force in the elbow joint in Example 9.4 is 407 N, asstated in the text.
27.
Two muscles in the back of the leg pull on the Achilles tendon asshown in
Figure 9.37. What total force do they exert?
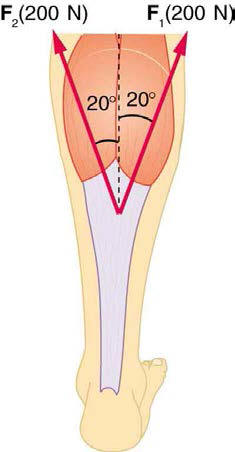
Figure 9.37
The Achilles tendon of the posterior leg serves to attach plantaris,gastrocnemius, and soleus muscles to calcaneus bone.
28.
The upper leg muscle (quadriceps) exerts a force of 1250 N, which iscarried by a tendon over the kneecap (the patella) at the angles shown in
Figure 9.38
. Find the direction and magnitude of the force exerted by thekneecap on the upper leg bone (the femur).
CHAPTER 9 | STATICS AND TORQUE 313
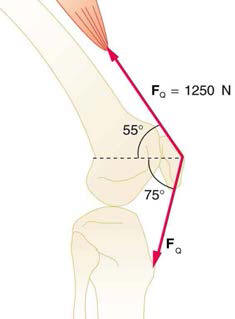
Figure 9.38
The knee joint works like a hinge to bend and straighten the lower leg. Itpermits a person to sit, stand, and pivot.
29.
A device for exercising the upper leg muscle is shown in Figure 9.39,together with a schematic representation of an equivalent lever system.
Calculate the force exerted by the upper leg muscle to lift the mass at a
constant speed. Explicitly show how you follow the steps in the Problem-
Solving Strategy for static equilibrium in
Applications of Statistics,Including Problem-Solving Strategies
.
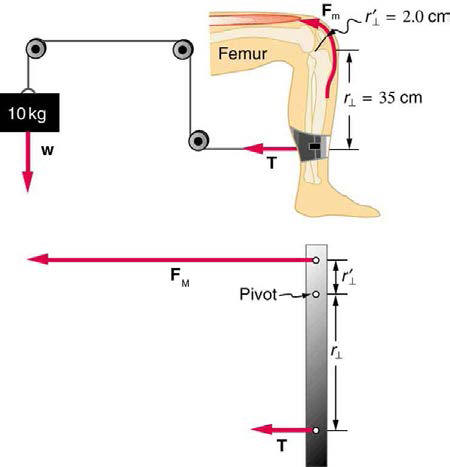
Figure 9.39
A mass is connected by pulleys and wires to the ankle in this exercisedevice.
30.
A person working at a drafting board may hold her head as shown inFigure 9.40
, requiring muscle action to support the head. The threemajor acting forces are shown. Calculate the direction and magnitude of
the force supplied by the upper vertebrae
FV to hold the headstationary, assuming that this force acts along a line through the center of
mass as do the weight and muscle force.
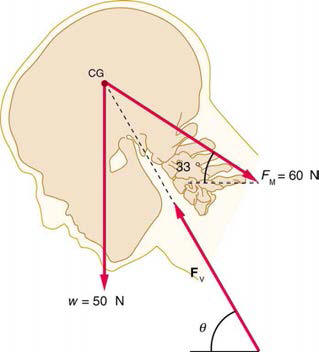
Figure 9.40
31.
We analyzed the biceps muscle example with the angle betweenforearm and upper arm set at
90º . Using the same numbers as inExample 9.4
, find the force exerted by the biceps muscle when the angleis
120º and the forearm is in a downward position.32.
Even when the head is held erect, as in Figure 9.41, its center ofmass is not directly over the principal point of support (the atlantooccipital
joint). The muscles at the back of the neck should therefore
exert a force to keep the head erect. That is why your head falls forward
when you fall asleep in the class. (a) Calculate the force exerted by these
muscles using the information in the figure. (b) What is the force exerted
by the pivot on the head?
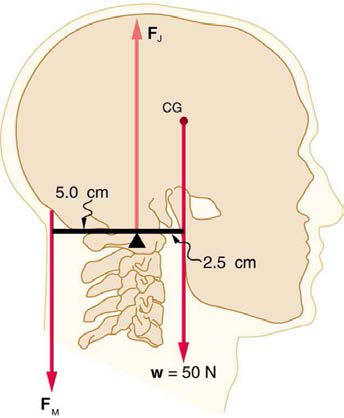 Figure 9.41
Figure 9.41
requiring muscle action to hold the head erect. A simplified lever system is shown.
33.
A 75-kg man stands on his toes by exerting an upward force throughthe Achilles tendon, as in
Figure 9.42. (a) What is the force in theAchilles tendon if he stands on one foot? (b) Calculate the force at the
pivot of the simplified lever system shown—that force is representative of
forces in the ankle joint.
314 CHAPTER 9 | STATICS AND TORQUE
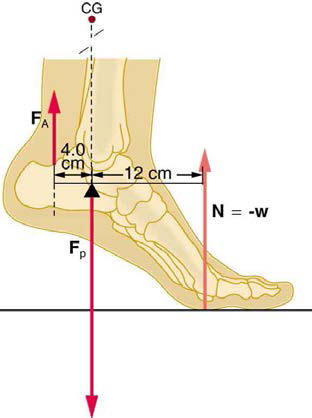
Figure 9.42
The muscles in the back of the leg pull the Achilles tendon when onestands on one’s toes. A simplified lever system is shown.
34.
A father lifts his child as shown in Figure 9.43. What force should theupper leg muscle exert to lift the child at a constant speed?
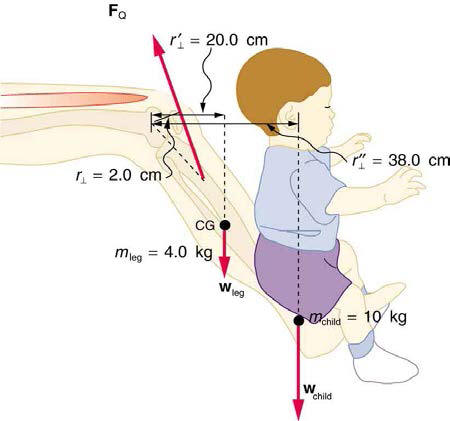
Figure 9.43
A child being lifted by a father’s lower leg.35.
Unlike most of the other muscles in our bodies, the masseter musclein the jaw, as illustrated in
Figure 9.44, is attached relatively far from thejoint, enabling large forces to be exerted by the back teeth. (a) Using the
information in the figure, calculate the force exerted by the teeth on the
bullet. (b) Calculate the force on the joint.
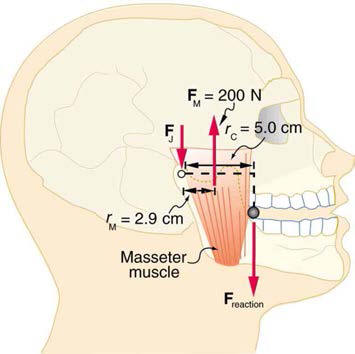
Figure 9.44
A person clenching a bullet between his teeth.36. Integrated Concepts
Suppose we replace the 4.0-kg book in
Exercise 9.31 of the bicepsmuscle with an elastic exercise rope that obeys Hooke’s Law. Assume its
force constant
k = 600 N/m . (a) How much is the rope stretched (pastequilibrium) to provide the same force
FB as in this example? Assumethe rope is held in the hand at the same location as the book. (b) What
force is on the biceps muscle if the exercise rope is pulled straight up so
that the forearm makes an angle of
25º with the horizontal? Assume thebiceps muscle is still perpendicular to the forearm.
37.
(a) What force should the woman in Figure 9.45 exert on the floorwith each hand to do a push-up? Assume that she moves up at a
constant speed. (b) The triceps muscle at the back of her upper arm has
an effective lever arm of 1.75 cm, and she exerts force on the floor at a
horizontal distance of 20.0 cm from the elbow joint. Calculate the
magnitude of the force in each triceps muscle, and compare it to her
weight. (c) How much work does she do if her center of mass rises 0.240
m? (d) What is her useful power output if she does 25 pushups in one
minute?
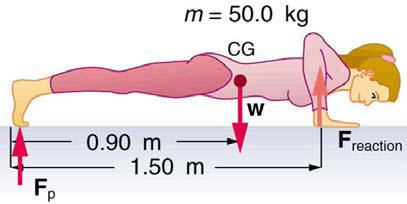
Figure 9.45
A woman doing pushups.38.
You have just planted a sturdy 2-m-tall palm tree in your front lawn foryour mother’s birthday. Your brother kicks a 500 g ball, which hits the top
of the tree at a speed of 5 m/s and stays in contact with it for 10 ms. The
ball falls to the ground near the base of the tree and the recoil of the tree
is minimal. (a) What is the force on the tree? (b) The length of the sturdy
section of the root is only 20 cm. Furthermore, the soil around the roots is
loose and we can assume that an effective force is applied at the tip of
the 20 cm length. What is the effective force exerted by the end of the tip
of the root to keep the tree from toppling? Assume the tree will be
uprooted rather than bend. (c) What could you have done to ensure that
the tree does not uproot easily?
39. Unreasonable Results
Suppose two children are using a uniform seesaw that is 3.00 m long and
has its center of mass over the pivot. The first child has a mass of 30.0
kg and sits 1.40 m from the pivot. (a) Calculate where the second 18.0 kg
child must sit to balance the seesaw. (b) What is unreasonable about the
result? (c) Which premise is unreasonable, or which premises are
inconsistent?
40. Construct Your Own Problem
Consider a method for measuring the mass of a person’s arm in
anatomical studies. The subject lies on her back, extends her relaxed
arm to the side and two scales are placed below the arm. One is placed
under the elbow and the other under the back of her hand. Construct a
problem in which you calculate the mass of the arm and find its center of
mass based on the scale readings and the distances of the scales from
the shoulder joint. You must include a free body diagram of the arm to
direct the analysis. Consider changing the position of the scale under the
hand to provide more information, if needed. You may
10.1 Angular Acceleration
1.
At its peak, a tornado is 60.0 m in diameter and carries 500 km/hwinds. What is its angular velocity in revolutions per second?
2. Integrated Concepts
An ultracentrifuge accelerates from rest to 100,000 rpm in 2.00 min. (a)
What is its angular acceleration in
rad/s2 ? (b) What is the tangentialacceleration of a point 9.50 cm from the axis of rotation? (c) What is the
radial acceleration in
m/s2 and multiples of g of this point at full rpm?3. Integrated Concepts
You have a grindstone (a disk) that is 90.0 kg, has a 0.340-m radius, and
is turning at 90.0 rpm, and you press a steel axe against it with a radial
force of 20.0 N. (a) Assuming the kinetic coefficient of friction between
steel and stone is 0.20, calculate the angular acceleration of the
grindstone. (b) How many turns will the stone make before coming to
rest?
4. Unreasonable Results
You are told that a basketball player spins the ball with an angular
acceleration of
100 rad/s2 . (a) What is the ball’s final angular velocity ifthe ball starts from rest and the acceleration lasts 2.00 s? (b) What is
unreasonable about the result? (c) Which premises are unreasonable or
inconsistent?
10.2 Kinematics of Rotational Motion
5.
With the aid of a string, a gyroscope is accelerated from rest to 32rad/s in 0.40 s.
(a) What is its angular acceleration in rad/s2?
(b) How many revolutions does it go through in the process?
6.
Suppose a piece of dust finds itself on a CD. If the spin rate of the CDis 500 rpm, and the piece of dust is 4.3 cm from the center, what is the
total distance traveled by the dust in 3 minutes? (Ignore accelerations
due to getting the CD rotating.)
7.
A gyroscope slows from an initial rate of 32.0 rad/s at a rate of0.700 rad/s
2 .(a) How long does it take to come to rest?
(b) How many revolutions does it make before stopping?
8.
During a very quick stop, a car decelerates at 7.00 m/s2 .(a) What is the angular acceleration of its 0.280-m-radius tires, assuming
they do not slip on the pavement?
(b) How many revolutions do the tires make before coming to rest, given
their initial angular velocity is
95.0 rad/s ?(c) How long does the car take to stop completely?
(d) What distance does the car travel in this time?
(e) What was the car’s initial velocity?
(f) Do the values obtained seem reasonable, considering that this stop
happens very quickly?

Figure 10.37
Yo-yos are amusing toys that display significant physics and areengineered to enhance performance based on physical laws. (credit: Beyond Neon,
Flickr)
9.
Everyday application: Suppose a yo-yo has a center shaft that has a0.250 cm radius and that its string is being pulled.
(a) If the string is stationary and the yo-yo accelerates away from it at a
rate of
1.50 m/s2 , what is the angular acceleration of the yo-yo?(b) What is the angular velocity after 0.750 s if it starts from rest?
(c) The outside radius of the yo-yo is 3.50 cm. What is the tangential
acceleration of a point on its edge?
10.3 Dynamics of Rotational Motion: Rotational Inertia
10.
This problem considers additional aspects of example Calculatingthe Effect of Mass Distribution on a Merry-Go-Round
. (a) How longdoes it take the father to give the merry-go-round and child an angular
velocity of 1.50 rad/s? (b) How many revolutions must he go through to
generate this velocity? (c) If he exerts a slowing force of 300 N at a
radius of 1.35 m, how long would it take him to stop them?
11.
Calculate the moment of inertia of a skater given the followinginformation. (a) The 60.0-kg skater is approximated as a cylinder that has
a 0.110-m radius. (b) The skater with arms extended is approximately a
cylinder that is 52.5 kg, has a 0.110-m radius, and has two 0.900-m-long
arms which are 3.75 kg each and extend straight out from the cylinder
like rods rotated about their ends.
12.
The triceps muscle in the back of the upper arm extends the forearm.This muscle in a professional boxer exerts a force of
2.00×103 N withan effective perpendicular lever arm of 3.00 cm, producing an angular
acceleration of the forearm of
120 rad/s2 . What is the moment of inertiaof the boxer’s forearm?
13.
A soccer player extends her lower leg in a kicking motion by exertinga force with the muscle above the knee in the front of her leg. She
produces an angular acceleration of
30.00 rad/s2 and her lower leg hasa moment of inertia of
0.750 kg ⋅ m2 . What is the force exerted by themuscle if its effective perpendicular lever arm is 1.90 cm?
14.
Suppose you exert a force of 180 N tangential to a 0.280-m-radius75.0-kg grindstone (a solid disk).
(a)What torque is exerted? (b) What is the angular acceleration assuming
negligible opposing friction? (c) What is the angular acceleration if there
is an opposing frictional force of 20.0 N exerted 1.50 cm from the axis?
15.
Consider the 12.0 kg motorcycle wheel shown in Figure 10.38.Assume it to be approximately an annular ring with an inner radius of
0.280 m and an outer radius of 0.330 m. The motorcycle is on its center
stand, so that the wheel can spin freely. (a) If the drive chain exerts a
force of 2200 N at a radius of 5.00 cm, what is the angular acceleration of
the wheel? (b) What is the tangential acceleration of a point on the outer
edge of the tire? (c) How long, starting from rest, does it take to reach an
angular velocity of 80.0 rad/s?
352 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
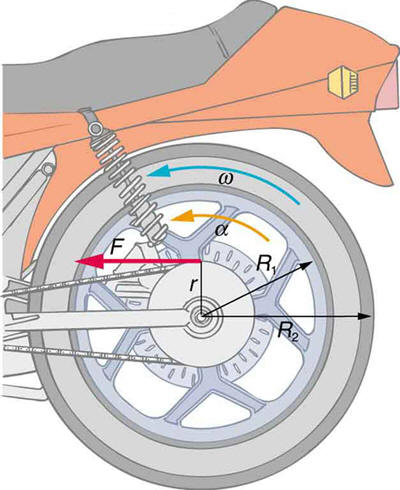
Figure 10.38
A motorcycle wheel has a moment of inertia approximately that of anannular ring.
16.
Zorch, an archenemy of Superman, decides to slow Earth’s rotationto once per 28.0 h by exerting an opposing force at and parallel to the
equator. Superman is not immediately concerned, because he knows
Zorch can only exert a force of
4.00×107 N (a little greater than aSaturn V rocket’s thrust). How long must Zorch push with this force to
accomplish his goal? (This period gives Superman time to devote to
other villains.) Explicitly show how you follow the steps found in
Problem-Solving Strategy for Rotational Dynamics
.17.
An automobile engine can produce 200 N · m of torque. Calculate theangular acceleration produced if 95.0% of this torque is applied to the
drive shaft, axle, and rear wheels of a car, given the following information.
The car is suspended so that the wheels can turn freely. Each wheel acts
like a 15.0 kg disk that has a 0.180 m radius. The walls of each tire act
like a 2.00-kg annular ring that has inside radius of 0.180 m and outside
radius of 0.320 m. The tread of each tire acts like a 10.0-kg hoop of
radius 0.330 m. The 14.0-kg axle acts like a rod that has a 2.00-cm
radius. The 30.0-kg drive shaft acts like a rod that has a 3.20-cm radius.
18.
Starting with the formula for the moment of inertia of a rod rotatedaround an axis through one end perpendicular to its length
⎛⎝
I
= Mℓ 2 / 3⎞⎠, prove that the moment of inertia of a rod rotated about
an axis through its center perpendicular to its length is
I = Mℓ 2 / 12 .You will find the graphics in
Figure 10.12 useful in visualizing theserotations.
19. Unreasonable Results
A gymnast doing a forward flip lands on the mat and exerts a 500-N · m
torque to slow and then reverse her angular velocity. Her initial angular
velocity is 10.0 rad/s, and her moment of inertia is
0.050 kg ⋅ m2 . (a)What time is required for her to exactly reverse her spin? (b) What is
unreasonable about the result? (c) Which premises are unreasonable or
inconsistent?
20. Unreasonable Results
An advertisement claims that an 800-kg car is aided by its 20.0-kg
flywheel, which can accelerate the car from rest to a speed of 30.0 m/s.
The flywheel is a disk with a 0.150-m radius. (a) Calculate the angular
velocity the flywheel must have if 95.0% of its rotational energy is used to
get the car up to speed. (b) What is unreasonable about the result? (c)
Which premise is unreasonable or which premises are inconsistent?
10.4 Rotational Kinetic Energy: Work and Energy
Revisited
21.
This problem considers energy and work aspects of Example10.7
—use data from that example as needed. (a) Calculate the rotationalkinetic energy in the merry-go-round plus child when they have an
angular velocity of 20.0 rpm. (b) Using energy considerations, find the
number of revolutions the father will have to push to achieve this angular
velocity starting from rest. (c) Again, using energy considerations,
calculate the force the father must exert to stop the merry-go-round in
two revolutions
22.
What is the final velocity of a hoop that rolls without slipping down a5.00-m-high hill, starting from rest?
23.
(a) Calculate the rotational kinetic energy of Earth on its axis. (b)What is the rotational kinetic energy of Earth in its orbit around the Sun?
24.
Calculate the rotational kinetic energy in the motorcycle wheel(
Figure 10.38) if its angular velocity is 120 rad/s.25.
A baseball pitcher throws the ball in a motion where there is rotationof the forearm about the elbow joint as well as other movements. If the
linear velocity of the ball relative to the elbow joint is 20.0 m/s at a
distance of 0.480 m from the joint and the moment of inertia of the
forearm is
0.500 kg ⋅ m2 , what is the rotational kinetic energy of theforearm?
26.
While punting a football, a kicker rotates his leg about the hip joint.The moment of inertia of the leg is
3.75 kg ⋅ m2 and its rotationalkinetic energy is 175 J. (a) What is the angular velocity of the leg? (b)
What is the velocity of tip of the punter’s shoe if it is 1.05 m from the hip
joint? (c) Explain how the football can be given a velocity greater than the
tip of the shoe (necessary for a decent kick distance).
27.
A bus contains a 1500 kg flywheel (a disk that has a 0.600 m radius)and has a total mass of 10,000 kg. (a) Calculate the angular velocity the
flywheel must have to contain enough energy to take the bus from rest to
a speed of 20.0 m/s, assuming 90.0% of the rotational kinetic energy can
be transformed into translational energy. (b) How high a hill can the bus
climb with this stored energy and still have a speed of 3.00 m/s at the top
of the hill? Explicitly show how you follow the steps in the
Problem-Solving Strategy for Rotational Energy
.28.
A ball with an initial velocity of 8.00 m/s rolls up a hill without slipping.Treating the ball as a spherical shell, calculate the vertical height it
reaches. (b) Repeat the calculation for the same ball if it slides up the hill
without rolling.
29.
While exercising in a fitness center, a man lies face down on a benchand lifts a weight with one lower leg by contacting the muscles in the
back of the upper leg. (a) Find the angular acceleration produced given
the mass lifted is 10.0 kg at a distance of 28.0 cm from the knee joint, the
moment of inertia of the lower leg is
0.900 kg ⋅ m2 , the muscle force is1500 N, and its effective perpendicular lever arm is 3.00 cm. (b) How
much work is done if the leg rotates through an angle of
20.0º with aconstant force exerted by the muscle?
30.
To develop muscle tone, a woman lifts a 2.00-kg weight held in herhand. She uses her biceps muscle to flex the lower arm through an angle
of
60.0º . (a) What is the angular acceleration if the weight is 24.0 cmfrom the elbow joint, her forearm has a moment of inertia of
0.250 kg ⋅ m
2 , and the muscle force is 750 N at an effectiveperpendicular lever arm of 2.00 cm? (b) How much work does she do?
31.
Consider two cylinders that start down identical inclines from restexcept that one is frictionless. Thus one cylinder rolls without slipping,
while the other slides frictionlessly without rolling. They both travel a short
distance at the bottom and then start up another incline. (a) Show that
they both reach the same height on the other incline, and that this height
is equal to their original height. (b) Find the ratio of the time the rolling
cylinder takes to reach the height on the second incline to the time the
sliding cylinder takes to reach the height on the second incline. (c)
Explain why the time for the rolling motion is greater than that for the
sliding motion.
32.
What is the moment of inertia of an object that rolls without slippingdown a 2.00-m-high incline starting from rest, and has a final velocity of
6.00 m/s? Express the moment of inertia as a multiple of
MR2 , whereM
is the mass of the object and R is its radius.33.
Suppose a 200-kg motorcycle has two wheels like, the onedescribed in Problem 10.15
and is heading toward a hill at a speed ofCHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 353
30.0 m/s. (a) How high can it coast up the hill, if you neglect friction? (b)
How much energy is lost to friction if the motorcycle only gains an altitude
of 35.0 m before coming to rest?
34.
In softball, the pitcher throws with the arm fully extended (straight atthe elbow). In a fast pitch the ball leaves the hand with a speed of 139
km/h. (a) Find the rotational kinetic energy of the pitcher’s arm given its
moment of inertia is
0.720 kg ⋅ m2 and the ball leaves the hand at adistance of 0.600 m from the pivot at the shoulder. (b) What force did the
muscles exert to cause the arm to rotate if their effective perpendicular
lever arm is 4.00 cm and the ball is 0.156 kg?
35. Construct Your Own Problem
Consider the work done by a spinning skater pulling her arms in to
increase her rate of spin. Construct a problem in which you calculate the
work done with a “force multiplied by distance” calculation and compare it
to the skater’s increase in kinetic energy.
10.5 Angular Momentum and Its Conservation
36.
(a) Calculate the angular momentum of the Earth in its orbit aroundthe Sun.
(b) Compare this angular momentum with the angular momentum of
Earth on its axis.
37.
(a) What is the angular momentum of the Moon in its orbit aroundEarth?
(b) How does this angular momentum compare with the angular
momentum of the Moon on its axis? Remember that the Moon keeps one
side toward Earth at all times.
(c) Discuss whether the values found in parts (a) and (b) seem consistent
with the fact that tidal effects with Earth have caused the Moon to rotate
with one side always facing Earth.
38.
Suppose you start an antique car by exerting a force of 300 N on itscrank for 0.250 s. What angular momentum is given to the engine if the
handle of the crank is 0.300 m from the pivot and the force is exerted to
create maximum torque the entire time?
39.
A playground merry-go-round has a mass of 120 kg and a radius of1.80 m and it is rotating with an angular velocity of 0.500 rev/s. What is
its angular velocity after a 22.0-kg child gets onto it by grabbing its outer
edge? The child is initially at rest.
40.
Three children are riding on the edge of a merry-go-round that is 100kg, has a 1.60-m radius, and is spinning at 20.0 rpm. The children have
masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg
moves to the center of the merry-go-round, what is the new angular
velocity in rpm?
41.
(a) Calculate the angular momentum of an ice skater spinning at 6.00rev/s given his moment of inertia is
0.400 kg ⋅ m2 . (b) He reduces hisrate of spin (his angular velocity) by extending his arms and increasing
his moment of inertia. Find the value of his moment of inertia if his
angular velocity decreases to 1.25 rev/s. (c) Suppose instead he keeps
his arms in and allows friction of the ice to slow him to 3.00 rev/s. What
average torque was exerted if this takes 15.0 s?
42.
Consider the Earth-Moon system. Construct a problem in which youcalculate the total angular momentum of the system including the spins of
the Earth and the Moon on their axes and the orbital angular momentum
of the Earth-Moon system in its nearly monthly rotation. Calculate what
happens to the Moon’s orbital radius if the Earth’s rotation decreases due
to tidal drag. Among the things to be considered are the amount by which
the Earth’s rotation slows and the fact that the Moon will continue to have
one side always facing the Earth.
10.6 Collisions of Extended Bodies in Two Dimensions
43.
Repeat Example 10.15 in which the disk strikes and adheres to thestick 0.100 m from the nail.
44.
Repeat Example 10.15 in which the disk originally spins clockwise at1000 rpm and has a radius of 1.50 cm.
45.
Twin skaters approach one another as shown in Figure 10.39 andlock hands. (a) Calculate their final angular velocity, given each had an
initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg,
and each has a center of mass located 0.800 m from their locked hands.
You may approximate their moments of inertia to be that of point masses
at this radius. (b) Compare the initial kinetic energy and final kinetic
energy.
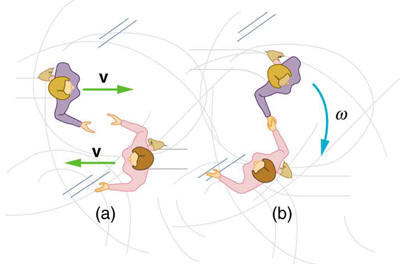
Figure 10.39
Twin skaters approach each other with identical speeds. Then, theskaters lock hands and spin.
46.
Suppose a 0.250-kg ball is thrown at 15.0 m/s to a motionless personstanding on ice who catches it with an outstretched arm as shown in
Figure 10.40
.(a) Calculate the final linear velocity of the person, given his mass is 70.0
kg.
(b) What is his angular velocity if each arm is 5.00 kg? You may treat his
arms as uniform rods (each has a length of 0.900 m) and the rest of his
body as a uniform cylinder of radius 0.180 m. Neglect the effect of the
ball on his center of mass so that his center of mass remains in his
geometrical center.
(c) Compare the initial and final total kinetic energies.
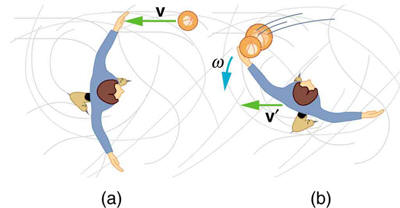
Figure 10.40
The figure shows the overhead view of a person standing motionless onice about to catch a ball. Both arms are outstretched. After catching the ball, the
skater recoils and rotates.
47.
Repeat Example 10.15 in which the stick is free to have translationalmotion as well as rotational motion.
10.7 Gyroscopic Effects: Vector Aspects of Angular
Momentum
48. Integrated Concepts
The axis of Earth makes a 23.5° angle with a direction perpendicular to
the plane of Earth’s orbit. As shown in
Figure 10.41, this axis precesses,making one complete rotation in 25,780 y.
(a) Calculate the change in angular momentum in half this time.
(b) What is the average torque producing this change in angular
momentum?
(c) If this torque were created by a single force (it is not) acting at the
most effective point on the equator, what would its magnitude be?
354 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
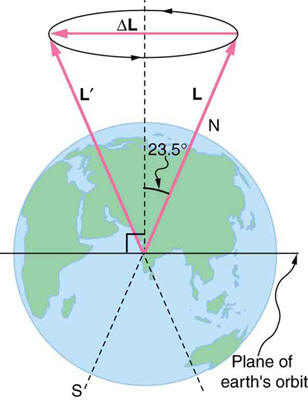
Figure 10.41
The Earth’s axis slowly precesses, always making an angle of 23.5° withthe direction perpendicular to the plane of Earth’s orbit. The change in angular
momentum for the two shown positions is quite large, although the magnitude
L isunchanged.
16.1 Hooke’s Law: Stress and Strain Revisited
1.
Fish are hung on a spring scale to determine their mass (mostfishermen feel no obligation to truthfully report the mass).
(a) What is the force constant of the spring in such a scale if it the spring
stretches 8.00 cm for a 10.0 kg load?
(b) What is the mass of a fish that stretches the spring 5.50 cm?
(c) How far apart are the half-kilogram marks on the scale?
2.
It is weigh-in time for the local under-85-kg rugby team. The bathroomscale used to assess eligibility can be described by Hooke’s law and is
depressed 0.75 cm by its maximum load of 120 kg. (a) What is the
spring’s effective spring constant? (b) A player stands on the scales and
depresses it by 0.48 cm. Is he eligible to play on this under-85 kg team?
3.
One type of BB gun uses a spring-driven plunger to blow the BB fromits barrel. (a) Calculate the force constant of its plunger’s spring if you
must compress it 0.150 m to drive the 0.0500-kg plunger to a top speed
of 20.0 m/s. (b) What force must be exerted to compress the spring?
4.
(a) The springs of a pickup truck act like a single spring with a forceconstant of
1.30×105 N/m . By how much will the truck be depressedby its maximum load of 1000 kg?
(b) If the pickup truck has four identical springs, what is the force
constant of each?
5.
When an 80.0-kg man stands on a pogo stick, the spring iscompressed 0.120 m.
(a) What is the force constant of the spring? (b) Will the spring be
compressed more when he hops down the road?
6.
A spring has a length of 0.200 m when a 0.300-kg mass hangs from it,and a length of 0.750 m when a 1.95-kg mass hangs from it. (a) What is
the force constant of the spring? (b) What is the unloaded length of the
spring?
16.2 Period and Frequency in Oscillations
7.
What is the period of 60.0 Hz electrical power?8.
If your heart rate is 150 beats per minute during strenuous exercise,what is the time per beat in units of seconds?
9.
Find the frequency of a tuning fork that takes 2.50×10−3 s tocomplete one oscillation.
10.
A stroboscope is set to flash every 8.00×10−5 s . What is thefrequency of the flashes?
11.
A tire has a tread pattern with a crevice every 2.00 cm. Each crevicemakes a single vibration as the tire moves. What is the frequency of
these vibrations if the car moves at 30.0 m/s?
12. Engineering Application
Each piston of an engine makes a sharp sound every other revolution of
the engine. (a) How fast is a race car going if its eight-cylinder engine
emits a sound of frequency 750 Hz, given that the engine makes 2000
revolutions per kilometer? (b) At how many revolutions per minute is the
engine rotating?
16.3 Simple Harmonic Motion: A Special Periodic
Motion
13.
A type of cuckoo clock keeps time by having a mass bouncing on aspring, usually something cute like a cherub in a chair. What force
constant is needed to produce a period of 0.500 s for a 0.0150-kg mass?
14.
If the spring constant of a simple harmonic oscillator is doubled, bywhat factor will the mass of the system need to change in order for the
frequency of the motion to remain the same?
15.
By how much leeway (both percentage and mass) would you have inthe selection of the mass of the object in the previous problem if you did
not wish the new period to be greater than 2.01 s or less than 1.99 s?
16.
A 0.500-kg mass suspended from a spring oscillates with a period of1.50 s. How much mass must be added to the object to change the
period to 2.00 s?
17.
Suppose you attach the object with mass m to a vertical springoriginally at rest, and let it bounce up and down. You release the object
from rest at the spring’s original rest length. (a) Show that the spring
exerts an upward force of
2.00 mg on the object at its lowest point. (b)If the spring has a force constant of
10.0 N/m and a 0.25-kg-massobject is set in motion as described, find the amplitude of the oscillations.
(c) Find the maximum velocity.
18.
A diver on a diving board is undergoing simple harmonic motion. Hermass is 55.0 kg and the period of her motion is 0.800 s. The next diver is
a male whose period of simple harmonic oscillation is 1.05 s. What is his
mass if the mass of the board is negligible?
19.
Suppose a diving board with no one on it bounces up and down in asimple harmonic motion with a frequency of 4.00 Hz. The board has an
effective mass of 10.0 kg. What is the frequency of the simple harmonic
motion of a 75.0-kg diver on the board?
20.
Figure 16.46
This child’s toy relies on springs to keep infants entertained. (credit: ByHumboldthead, Flickr)
The device pictured in
Figure 16.46 entertains infants while keepingthem from wandering. The child bounces in a harness suspended from a
door frame by a spring constant.
(a) If the spring stretches 0.250 m while supporting an 8.0-kg child, what
is its spring constant?
(b) What is the time for one complete bounce of this child? (c) What is the
child’s maximum velocity if the amplitude of her bounce is 0.200 m?
21.
A 90.0-kg skydiver hanging from a parachute bounces up and downwith a period of 1.50 s. What is the new period of oscillation when a
second skydiver, whose mass is 60.0 kg, hangs from the legs of the first,
as seen in
Figure 16.47.584 CHAPTER 16 | OSCILLATORY MOTION AND WAVES

Figure 16.47
The oscillations of one skydiver are about to be affected by a secondskydiver. (credit: U.S. Army, www.army.mil)
16.4 The Simple Pendulum
As usual, the acceleration due to gravity in these problems is taken
to be
g = 9.80 m / s2 , unless otherwise specified.22.
What is the length of a pendulum that has a period of 0.500 s?23.
Some people think a pendulum with a period of 1.00 s can be drivenwith “mental energy” or psycho kinetically, because its period is the same
as an average heartbeat. True or not, what is the length of such a
pendulum?
24.
What is the period of a 1.00-m-long pendulum?25.
How long does it take a child on a swing to complete one swing if hercenter of gravity is 4.00 m below the pivot?
26.
The pendulum on a cuckoo clock is 5.00 cm long. What is itsfrequency?
27.
Two parakeets sit on a swing with their combined center of mass 10.0cm below the pivot. At what frequency do they swing?
28.
(a) A pendulum with that has a period of 3.00000 s and that is locatedwhere the acceleration due to gravity is
9.79 m/s2 is moved to alocation where it the acceleration due to gravity is
9.82 m/s2 . What is itsnew period? (b) Explain why so many digits are needed in the value for
the period, based on the relation between the period and the acceleration
due to gravity.
29.
A pendulum with a period of 2.00000 s in one location⎛⎝
g
= 9.80 m/s2⎞⎠is moved to a new location where the period is now
1.99796 s. What is the acceleration due to gravity at its new location?
30.
(a) What is the effect on the period of a pendulum if you double itslength?
(b) What is the effect on the period of a pendulum if you decrease its
length by 5.00%?
31.
Find the ratio of the new/old periods of a pendulum if the pendulumwere transported from Earth to the Moon, where the acceleration due to
gravity is
1.63 m/s2 .32.
At what rate will a pendulum clock run on the Moon, where theacceleration due to gravity is
1.63 m/s2 , if it keeps time accurately onEarth? That is, find the time (in hours) it takes the clock’s hour hand to
make one revolution on the Moon.
33.
Suppose the length of a clock’s pendulum is changed by 1.000%,exactly at noon one day. What time will it read 24.00 hours later,
assuming it the pendulum has kept perfect time before the change? Note
that there are two answers, and perform the calculation to four-digit
precision.
34.
If a pendulum-driven clock gains 5.00 s/day, what fractional change inpendulum length must be made for it to keep perfect time?
16.5 Energy and the Simple Harmonic Oscillator
35.
The length of nylon rope from which a mountain climber is suspendedhas a force constant of
1.40×104 N/m .(a) What is the frequency at which he bounces, given his mass plus and
the mass of his equipment are 90.0 kg?
(b) How much would this rope stretch to break the climber’s fall if he freefalls
2.00 m before the rope runs out of slack? Hint: Use conservation of
energy.
(c) Repeat both parts of this problem in the situation where twice this
length of nylon rope is used.
36. Engineering Application
Near the top of the Citigroup Center building in New York City, there is an
object with mass of 4.00×105 kg on springs that have adjustable force
constants. Its function is to dampen wind-driven oscillations of the
building by oscillating at the same frequency as the building is being
driven—the driving force is transferred to the object, which oscillates
instead of the entire building. (a) What effective force constant should the
springs have to make the object oscillate with a period of 2.00 s? (b)
What energy is stored in the springs for a 2.00-m displacement from
equilibrium?
16.6 Uniform Circular Motion and Simple Harmonic
Motion
37.
(a)What is the maximum velocity of an 85.0-kg person bouncing on abathroom scale having a force constant of
1.50×106 N/m , if theamplitude of the bounce is 0.200 cm? (b)What is the maximum energy
stored in the spring?
38.
A novelty clock has a 0.0100-kg mass object bouncing on a springthat has a force constant of 1.25 N/m. What is the maximum velocity of
the object if the object bounces 3.00 cm above and below its equilibrium
position? (b) How many joules of kinetic energy does the object have at
its maximum velocity?
39.
At what positions is the speed of a simple harmonic oscillator half itsmaximum? That is, what values of
x / X give v = ±vmax / 2 , where Xis the amplitude of the motion?
40.
A ladybug sits 12.0 cm from the center of a Beatles music albumspinning at 33.33 rpm. What is the maximum velocity of its shadow on
the wall behind the turntable, if illuminated parallel to the record by the
parallel rays of the setting Sun?
16.7 Damped Harmonic Motion
41.
The amplitude of a lightly damped oscillator decreases by 3.0%during each cycle. What percentage of the mechanical energy of the
oscillator is lost in each cycle?
16.8 Forced Oscillations and Resonance
42.
How much energy must the shock absorbers of a 1200-kg cardissipate in order to damp a bounce that initially has a velocity of 0.800
m/s at the equilibrium position? Assume the car returns to its original
vertical position.
43.
If a car has a suspension system with a force constant of5.00×10
4 N/m , how much energy must the car’s shocks remove todampen an oscillation starting with a maximum displacement of 0.0750
m?
44.
(a) How much will a spring that has a force constant of 40.0 N/m bestretched by an object with a mass of 0.500 kg when hung motionless
from the spring? (b) Calculate the decrease in gravitational potential
energy of the 0.500-kg object when it descends this distance. (c) Part of
this gravitational energy goes into the spring. Calculate the energy stored
in the spring by this stretch, and compare it with the gravitational potential
energy. Explain where the rest of the energy might go.
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 585
45.
Suppose you have a 0.750-kg object on a horizontal surfaceconnected to a spring that has a force constant of 150 N/m. There is
simple friction between the object and surface with a static coefficient of
friction
μs = 0.100 . (a) How far can the spring be stretched withoutmoving the mass? (b) If the object is set into oscillation with an amplitude
twice the distance found in part (a), and the kinetic coefficient of friction is
μ
k = 0.0850 , what total distance does it travel before stopping?Assume it starts at the maximum amplitude.
46.
Engineering Application: A suspension bridge oscillates with aneffective force constant of
1.00×108 N/m . (a) How much energy isneeded to make it oscillate with an amplitude of 0.100 m? (b) If soldiers
march across the bridge with a cadence equal to the bridge’s natural
frequency and impart
1.00×104 J of energy each second, how longdoes it take for the bridge’s oscillations to go from 0.100 m to 0.500 m
amplitude?
16.9 Waves
47.
Storms in the South Pacific can create waves that travel all the way tothe California coast, which are 12,000 km away. How long does it take
them if they travel at 15.0 m/s?
48.
Waves on a swimming pool propagate at 0.750 m/s. You splash thewater at one end of the pool and observe the wave go to the opposite
end, reflect, and return in 30.0 s. How far away is the other end of the
pool?
49.
Wind gusts create ripples on the ocean that have a wavelength of5.00 cm and propagate at 2.00 m/s. What is their frequency?
50.
How many times a minute does a boat bob up and down on oceanwaves that have a wavelength of 40.0 m and a propagation speed of 5.00
m/s?
51.
Scouts at a camp shake the rope bridge they have just crossed andobserve the wave crests to be 8.00 m apart. If they shake it the bridge
twice per second, what is the propagation speed of the waves?
52.
What is the wavelength of the waves you create in a swimming pool ifyou splash your hand at a rate of 2.00 Hz and the waves propagate at
0.800 m/s?
53.
What is the wavelength of an earthquake that shakes you with afrequency of 10.0 Hz and gets to another city 84.0 km away in 12.0 s?
54.
Radio waves transmitted through space at 3.00×108 m/s by theVoyager spacecraft have a wavelength of 0.120 m. What is their
frequency?
55.
Your ear is capable of differentiating sounds that arrive at the ear just1.00 ms apart. What is the minimum distance between two speakers that
produce sounds that arrive at noticeably different times on a day when
the speed of sound is 340 m/s?
56.
(a) Seismographs measure the arrival times of earthquakes with aprecision of 0.100 s. To get the distance to the epicenter of the quake,
they compare the arrival times of S- and P-waves, which travel at
different speeds.
Figure 16.48) If S- and P-waves travel at 4.00 and 7.20km/s, respectively, in the region considered, how precisely can the
distance to the source of the earthquake be determined? (b) Seismic
waves from underground detonations of nuclear bombs can be used to
locate the test site and detect violations of test bans. Discuss whether
your answer to (a) implies a serious limit to such detection. (Note also
that the uncertainty is greater if there is an uncertainty in the propagation
speeds of the S- and P-waves.)

Figure 16.48
A seismograph as described in above problem.(credit: Oleg Alexandrov)16.10 Superposition and Interference
57.
A car has two horns, one emitting a frequency of 199 Hz and theother emitting a frequency of 203 Hz. What beat frequency do they
produce?
58.
The middle-C hammer of a piano hits two strings, producing beats of1.50 Hz. One of the strings is tuned to 260.00 Hz. What frequencies
could the other string have?
59.
Two tuning forks having frequencies of 460 and 464 Hz are strucksimultaneously. What average frequency will you hear, and what will the
beat frequency be?
60.
Twin jet engines on an airplane are producing an average soundfrequency of 4100 Hz with a beat frequency of 0.500 Hz. What are their
individual frequencies?
61.
A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s totravel the length of the Slinky and back again. (a) What is the speed of
the wave? (b) Using the same Slinky stretched to the same length, a
standing wave is created which consists of three antinodes and four
nodes. At what frequency must the Slinky be oscillating?
62.
Three adjacent keys on a piano (F, F-sharp, and G) are strucksimultaneously, producing frequencies of 349, 370, and 392 Hz. What
beat frequencies are produced by this discordant combination?
16.11 Energy in Waves: Intensity
63. Medical Application
Ultrasound of intensity 1.50×102 W/m2 is produced by the rectangular
head of a medical imaging device measuring 3.00 by 5.00 cm. What is its
power output?
64.
The low-frequency speaker of a stereo set has a surface area of0.05 m
2 and produces 1W of acoustical power. What is the intensity atthe speaker? If the speaker projects sound uniformly in all directions, at
what distance from the speaker is the intensity
0.1 W/m2 ?65.
To increase intensity of a wave by a factor of 50, by what factorshould the amplitude be increased?
66. Engineering Application
A device called an insolation meter is used to measure the intensity of
sunlight has an area of 100 cm2 and registers 6.50 W. What is the
intensity in W/m2 ?
67. Astronomy Application
Energy from the Sun arrives at the top of the Earth’s atmosphere with an
intensity of 1.30 kW/m2. How long does it take for 1.8×109 J to
arrive on an area of 1.00 m2 ?
586 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
68.
The low-frequency speaker of a stereo set has a surface area of0.05 m
2 and produces 1 W of acoustical power. What is the intensity atthe speaker? If the speaker projects sound uniformly in all directions, at
what distance from the speaker is the intensity
0.1 W/m2 ?69.
Suppose you have a device that extracts energy from ocean breakersin direct proportion to their intensity. If the device produces 10.0 kW of
power on a day when the breakers are 1.20 m high, how much will it
produce when they are 0.600 m high?
70. Engineering Application
(a) A photovoltaic array of (solar cells) is 10.0% efficient in gathering
solar energy and converting it to electricity. If the average intensity of
sunlight on one day is 700 W/m2, what area should your array have to
gather energy at the rate of 100 W? (b) What is the maximum cost of the
array if it must pay for itself in two years of operation averaging 10.0
hours per day? Assume that it earns money at the rate of 9.00 ¢ per
kilowatt-hour.
71.
A microphone receiving a pure sound tone feeds an oscilloscope,producing a wave on its screen. If the sound intensity is originally
2.00×10
–5 W/m2, but is turned up until the amplitude increases by30.0%, what is the new intensity?
72. Medical Application
(a) What is the intensity in W/m2 of a laser beam used to burn away
cancerous tissue that, when 90.0% absorbed, puts 500 J of energy into a
circular spot 2.00 mm in diameter in 4.00 s? (b) Discuss how this
intensity compares to the average intensity of sunlight (about 1 W/m2 )
and the implications that would have if the laser beam entered your eye.
Note how your answer depends on the time duration of the exposure.