Class Notes Physics I, 11/30/98
SHM of floating objects
A uniform cylindrical
buoy will, when pushed downward and released, bob up and down in response to
changes in the buoyant force, which we show constitutes a linear restoring force
F = - k x. We determine k experimentally by adding a known weight to the buoy
and observing the change in its equilibrium position, then theoretically by
determining the buoyant force corresponding to an additional immersion by
distance `dx. We compare experimental and theoretical results to the observed
period of motion.
When an object
rotating about a fixed axis experiences a linear restoring net torque `tau = - k
`theta, it will undergo simple harmonic motion with angular frequency 'omega `sqrt
( k / I), where I is its moment of inertia. We analyze the angular simple
harmonic motion of a floating rectangular piece of Styrofoam on which known
masses have been placed at known distances from the center of mass. We observe
the angular displacement resulting from a known torque and use this observation
to determine k. From the positions of the known masses we determine the moment
of inertia about the central axis of the rectangle. We determine the resulting
theoretical angular frequency and compare with the observed angular frequency of
the motion.
We note that a change
in the scale of the system (changing the dimensions of the Styrofoam and still
placing the washers at its corners), with no change in the masses of the washers
apparently results in no change in the period of motion. We analyze the scaling
factors involved and raise some questions about our results.
http://youtu.be/x959lOn5ph4
http://youtu.be/4djnL1I3BIM
Recall that simple
harmonic motion occurs when
a fixed mass m is subject to a net force F
= - k x when at position x
relative to its equilibrium position.. The angular frequency of the resulting
motion is `omega = `sqrt ( k
/ m ).
Buoyant Restoring Force
We begin by investigating the 'bobbing' motion of a buoy consisting of a
1/4-inch wooden dowel floating in water with a metal washer attached to one end.
- The function of the metal washer is to make the dowel float in a
vertical position.
The figure below depicts the (blue) dowel and washer floating in its
equilibrium position, and (red) in an lower equilibrium position when a .2 gram
weight is added on the top of the dowel.
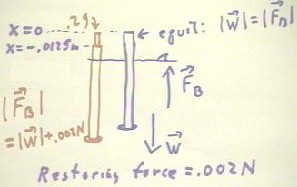
The dowel will, when undisturbed, float in an equilibrium position in which
the upward buoyant force Fb of the water on the dowel and washer is equal and
opposite to the weight W of the system.
- If the dowel is
immersed deeper in the water, the additional buoyant force on the newly
immersed segment of the dowel will constitute a restoring force tending to
push the dowel back toward its equilibrium position.
- If the dowel is
raised partially out of the water, the buoyant force decreases and does not
fully counter the gravitational force so that a net downward force now tends
to restore the system to its equilibrium position.
- If the dowel is
uniform, then the change in the buoyant force will be proportional to the
distance the dowel is raised or lowered from its equilibrium position.
- The magnitude of the restoring force will therefore be proportional to
the displacement from equilibrium, and we will have a linear restoring force
- The negative sign
reflects the fact that the net force is in the opposite direction to the
displacement of the system from its equilibrium position.
- That is, if the
system is displaced downward the additional buoyant force is upward and if
the system is displaced upward the reduced buoyant force results in a net
downward force.
Observing the Buoyant Restoring Force
We determine the velue of k for the restoring force by adding a .2 gram mass
to the top of the dowel.
- The result of the
gravitational force on this added mass is that the system sinks to a new
equilibrium position 1.25 cm, or .0125 m, below the original.
- Since the
gravitational force on a mass of .2 grams is .00196 N, we conclude that an
additional buoyant force of .00196 N (this value rounded to one significant
figure) is acting upward on the original system.
- Thus a displacement of -.0125 m results in a restoring force of .00196 N
(note that by the signs we have implicitly chosen the upward direction as
positive).
We therefore conclude that
the constant k of the relationship F = - kx is k = .157 N / m.
- We note that our
observation of the additional depth has perhaps a 10% margin of error, so
that the three apparently significant figures obtained for k are not in fact
all significant.

By weighing the dowel and
washer we determine that its mass is 5.5 grams, or .0055 kg.
- We therefore
conclude from the linearity of its restoring force that the system will tend
to undergo simple harmonic motion was a new frequency `omega = `sqrt(k/m) =
5.3 rad / s.
- Its period of SHM
will therefore be 2 `pi / (5.3 rad/s) = 1.2 sec, approximately.

This result is not in good
agreement with the period observed when the dowel is pushed downward then
released.
- We observed the
period to be the time required for the dowel to rise and fall.
- The observed
period was around .7 sec.
Calculating the
Buoyant Restoring Force
We now analyze the situation by calculating the change in the buoyant force
corresponding to immersion of an additional length `dx of the dowel. The
diameter of the dowel is 1/4 inch, which we easily convert to 6.35 mm.
- When an additional
segment of length `dx (shaded ingredient in the figure below) is immersed in
the water, the resulting buoyant force will by Archimedes' Principle be
equal to the weight of the water displaced.
- To find the weight
of the water displaced we find the volume of water displaced and multiplied
by the density of water.
- We displace a
volume `dV equal to that of a cylinder whose diameter is 6.35 mm and whose
altitude is `dx.
- This volume will
be equal to the product of the area `pi r^2 of the base of the cylinder and
its altitude `dx.
- Using half the diameter of the dowel as the radius, we find that `dV = A
`dx = 31 mm^2 `dx = 3.1 * 10^-5 m^2 `dx.
The weight of the water
displaced, and thus the restoring force will therefore have magnitude `rho g `dV,
so
- | `dF | = 1000 kg
/ m^3 * (9.8 m/s^2) * 3.1 * 10^-5 m^2 `dx = .3 N / m * `dx.
Since the direction of the
restoring forces opposite to the direction of `dx, we see that
We therefore conclude that
k = -`dF / `dx = 3 N / m (or more accurately .294 N/m).

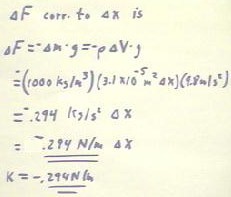
Using this theoretical
value of k we obtain `omega = 9.2 rad/s, so that the predicted period is T = .67
sec.
- This period is in
good agreement with the observed period.
- This should
motivate us to go back and repeat our observations to determine k
experimentally.
- We note that it is
a bit tricky to measure the displacement resulting from an added weight on
the top of the dowel and that our first attempt might have been somewhat
clumsy.
- We note also that
the motion of the dowel is not perfect SHM, since the frictional drag of the
water rapidly decreases the amplitude of the motion. As a result the actual
frequency will differ somewhat from the 'ideal' predicted frequency, which
did not take account of this drag factor.
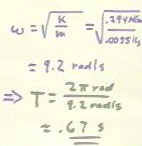
http://youtu.be/1Vc76t-4rl4
In class we spontaneously observed, as a result of one student's playful
exercise in balancing four washers at the corners of a barely floating CD jewel
box, another system consisting of a rectangular piece of Styrofoam approximately
8 cm by 10 cm by 3/4 inch (close to 2 cm) on which 8 washers are balanced near
the corners.
- When one end or
another is displaced downward then released the ends alternatively bob up
and down, with one end up when the other is down.
- This motion can be understood as rotation about an axis perpendicular to
the length of the rectangle and parallel to the water surface.
It will turn out that this motion constitutes angular simple harmonic motion.
- By analogy with
the simple harmonic motion of a pendulum, a weight on a spring or a bobbing
buoy, which are the result of the restoring force F = - kx, the present
system will be governed by a restoring torque of the form `tau
= -k `theta.
- That is, the system will experience a restoring torque `tau in response
to an angular displacement `d`theta, with the torque and angular
displacement related by `tau = - k `theta, where `theta is the angular
displacement from the equilibrium position.
Calculus-based note
justifying this analogy:
- The result of such
a restoring torque is that `alpha = -k `theta / I.
- Since `alpha =
d^2(`theta) / `dt^2, the second derivative of the angular position function
`theta, we obtain the differential equation identical except for the symbols
used for the variables to that we solved for the standard SHM situation.
- The details are in
the University Physics text.
The figure below depicts the situation.
- The total mass
added to each end of the system is 60 grams, corresponding to a set of two
15 g washers at each corner of the rectangle.
- The separation of the centers of mass of these washers is approximately
8 cm. This configuration is depicted in the upper right-hand corner of the
figure below.
In the upper left-hand corner we depict the fact that an additional 15 grams
at one end of the rectangle displaces the end of the rectangle .5 cm down into
the water.
- We can determine the 'torque constant' k if we can determine the torque
`d`tau of the 15 g weight and the angular displacement `d`theta
corresponding to the .5 cm displacement of the end of the rectangle.
The torque of the 15 g mass will be equal to the product of the force exerted
by gravity on that mass and the distance from the axis of rotation at which that
force is applied.
- The distance is
observed to be 4 cm.
- The torque is easily calculated as in the figure below to be `d`tau =
.006 N.
The angular displacement
corresponding to a .5 cm displacement at a distance of 5 cm from the axis of
rotation is `d`theta = tan^-1(.5 cm / 5 cm) = .1 rad.

We can now easily find k, as indicated below.
- By analogy with
linear SHM, we conjecture that since the moment of inertia I is analogous to
mass m (recall the two forms of Newton's Second Law F = ma and `tau = I
`alpha), for rotational SHM we should have `omega
= `sqrt( k / I ).
- This is in fact the case (241 students note that this follows from the
solution of the differential equation mentioned above).
Therefore from the relationship `omega = `sqrt(k / I) we predict the angular
frequency and therefore the period of the rotational SHM of the system.
- Ignoring the
relatively small moment of inertia of the Styrofoam rectangle, we calculate
the moment of inertia of just the washers.
- Making the
approximation that the mass of each washer is concentrated at its center, we
easily find the sum of the mr^2 contributions of the washers (each centered
at a point 4 cm from the axis of rotation) to be
- I = 8 * (.015 kg) * (.04 m)^2 = .12 kg * (.04 m) ^ 2 = .000192 kg
m^2.
I = .000192 kg m^2 and k =
.06 m N / rad imply `omega = 17.6 rad / s.
- You should verify
this result.
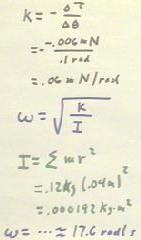
This angular frequency implies a period of .36 sec, as indicated in the
figure below.
A reasonably careful observation of 6 complete oscillations of the system
indicates a period of .4 sec, in good agreement with our prediction.
We might explain some of the discrepancy between observation and prediction
by including the moment of inertia of the Styrofoam, which we previously
neglected.
- It turns out that
the moment of inertia of the Styrofoam, calculated as a rod rotating about
its center, is only about 2 percent that of the washers.
- Since the angular
frequency was calculated using the square root of the moment of inertia,
adding the moment of inertia of the Styrofoam will change our prediction by
only about 1% and will not explain the discrepancy.
- A better explanation is the difficulty of accurately observing the
apparent .5 cm displacement of the end of the Styrofoam rectangle. There was
easily a 10% margin of error in that observation.

http://youtu.be/CUaqNXf_oW8
Effects of Change of Scale
It was observed that masurement of the period of a similar system with a
longer piece of Styrofoam (17 cm by 8 cm) and the same number of washers
resulted in very little change in the observed period. The effects of the change
in the scale of the system would be
- to increase the
distance of each washer from the center from 4 cm to 7.5 cm, which would
increase the moment of inertia by a factor of (7.5 / 4)^2
The change of scale would also result in a different value of k. The results
would be
- to change the angular displacement of the end resulting from the
addition of the 15 g washer by factor (4 / 7.5), since the distance from the
axis of rotation would change by factor 7.5 / 4
- to change the
torque associated with the 15 g washer by factor of (7.5 / 4)
- All this would change k = `d`tau / `d`theta by factor (7.5 / 4) / (4 /
7.5) = (7.5 / 4) ^ 2.
Since the moment of inertia I also changes by factor (7.5 / 4) ^ 2, we
conclude that k / I will remain unchanged.
- As result `omega = `sqrt(k / I) will remain unchanged.
In symbols we would say that changing the length of the system by factor c
will
- change its moment
of inertia by factor c^2 (recall that moment of inertia `sum (mr^2) is
proportional to the square of the distance of the masses from the axis of
rotation),
- change the angular
displacement corresponding to a given torque by factor 1/c,
- change the torque
itself by factor c, and therefore
- change k = `tau / `theta by factor c^2
The result would be to change both I and k by the same factor, c^2, resulting
in the no change in `omega = `sqrt( k / I ).
Or is this really the
case?
- Since there is
more Styrofoam to be submerged, would the displacement of the end due to the
addition of the 15 g mass also change by factor 1/c (4 / 7.5 in our
example)? And would not the width of the rectangle have an effect?
- If so what would
this do to our predicted angular frequency and period?
- How could we test
our alternative hypotheses?
"
