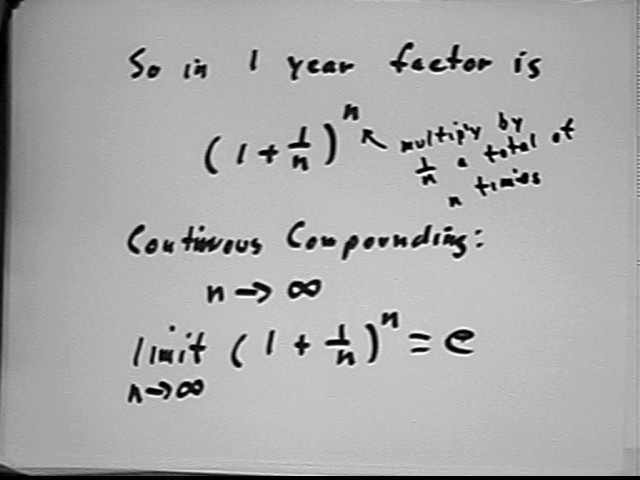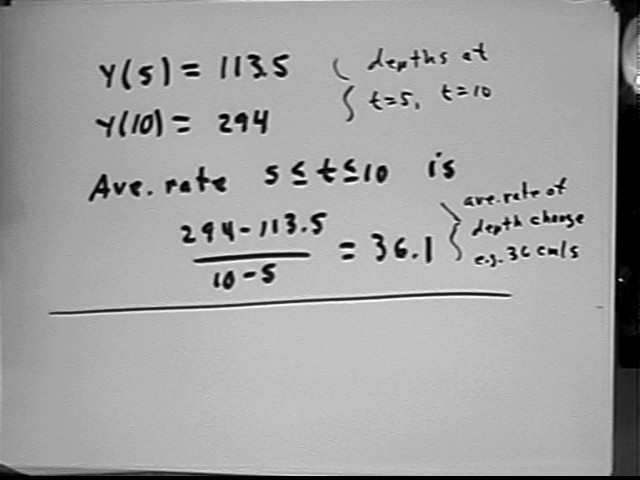
Calculus I Quiz 020907
The derivative of a t^3 + b t^2 + c t + d is 3 a t^2 + 2 b t + c.
SOLUTIONS
The derivative of a t^3 + b t^2 + c t + d is 3 a t^2 + 2 b t + c.
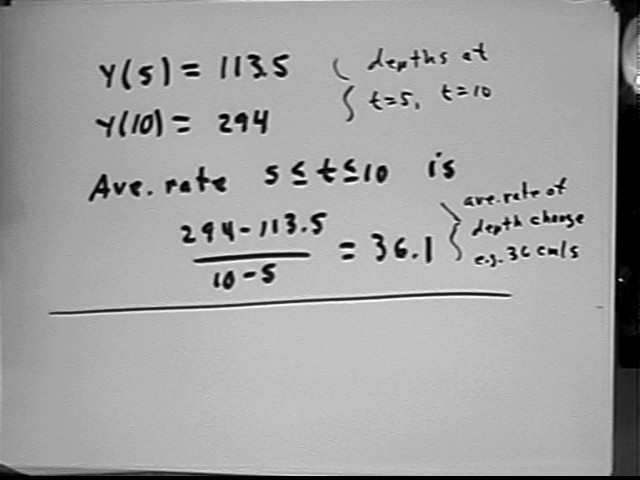
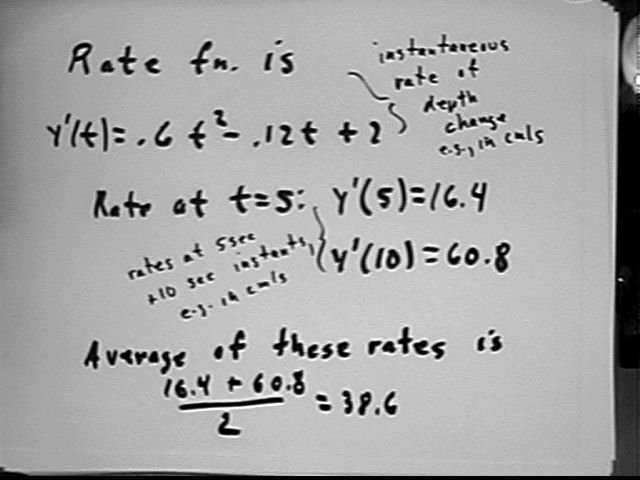

The rate function is quadratic, with a parabolic graph (note that y = a t^2 + b t + c has a vertex at t = -b / (2a), which pretty much follows from the Quadratic Formula, and that if you move 1 unit to the right or left of the vertex the y value will change by a). This graph of y ' vs. t is shown below.
The average of initial and final rates over an interval can be found on this graph by sketching a straight line segment joining the two corresponding points of the graph, then projecting from the midpoint of the time interval up to this segment and then across to the y ' axis. This approximation to the average rate y ' corresponds to a linear y ' vs. t function.
Since the graph of y ' vs. t is concave upward it lies below this straight-line segment. It follows that the actual average of y ' must be less than the straight-line average that corresponds to the average of initial and final rates.
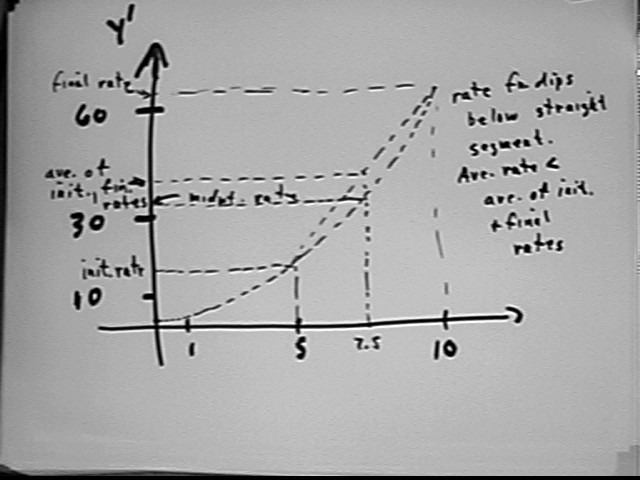
The midpoint rate is found by evaluating the rate function y ' at the midpoint clock time of 7.5 seconds. This midpoint rate is shown graphically in the figure above, and is calculated in the figure below.

We see that for this function midpt rate < ave rate < ave of init and final rates. It is worth thinking about the question posed above.
The general exponential function y = A * b^t has the properties outlined below:
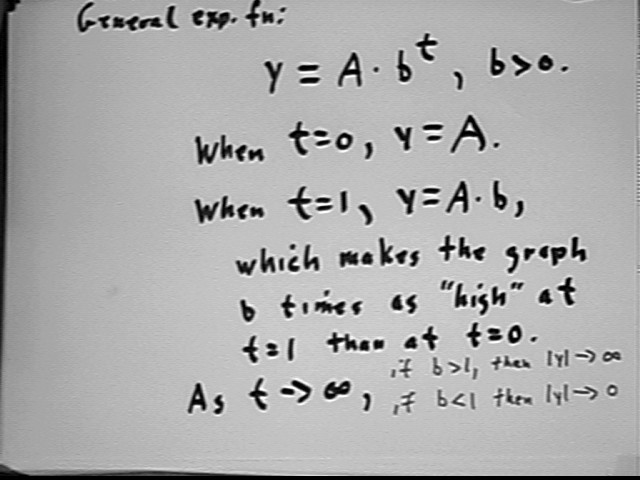
Examples illustrate these properties and others:

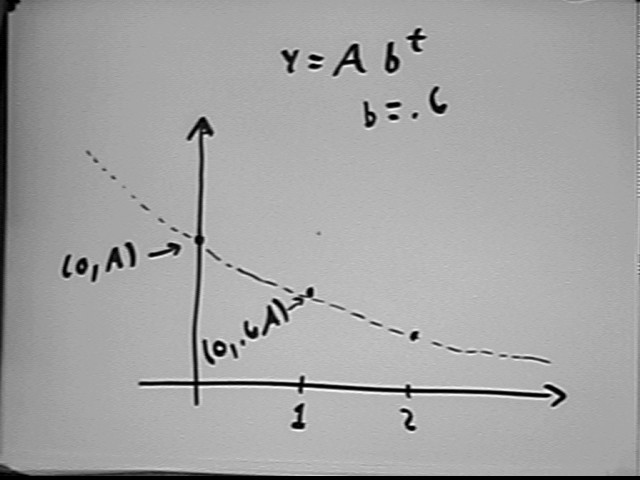
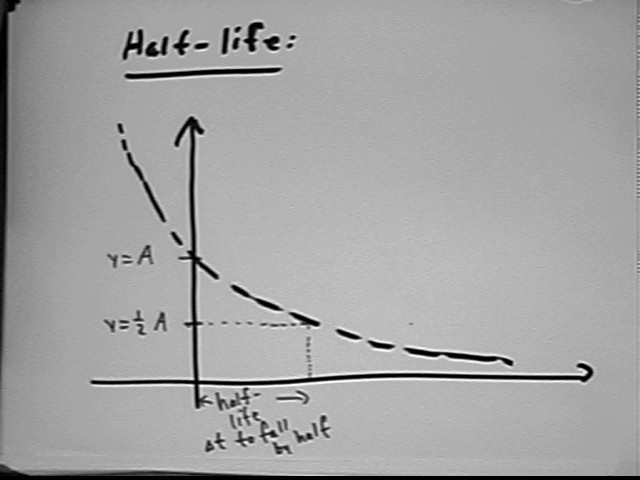
The question was asked 'how do we actually apply that e thing', or something like that.