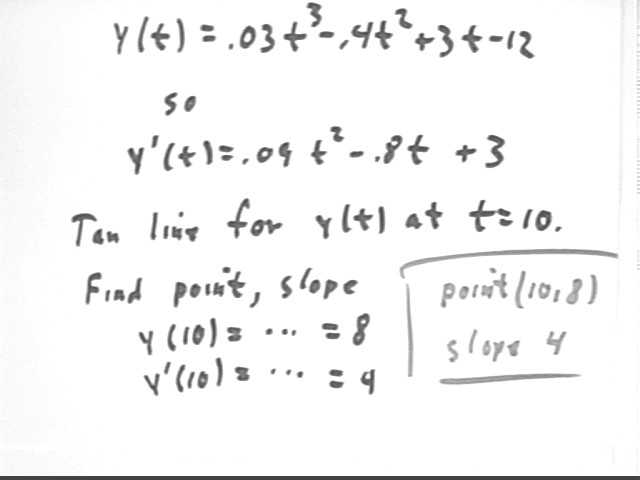
Calculus I Quiz 09/13/02
1. What is the equation of the line tangent to the curve y = .03 t^3 - .4 t^2 + 3 t - 12 at the t = 10 point of the curve?
SOLUTION:
We get a point on the y vs. t curve by plugging t = 10 into the formula for y(t). We get the slope by finding the slope function y ' (t) and plugging in t = 10. Then we find the equation of the straight line through our point with the required slope.
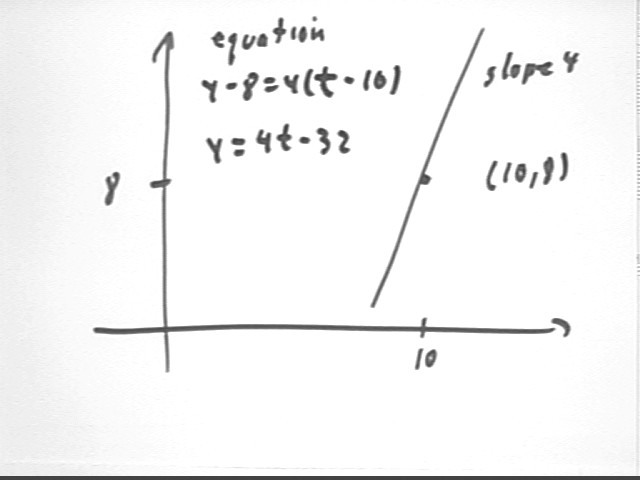
How closely does this tangent line approximate the value of y at t = 10.4?
SOLUTION:
We evaluate the tangent-line function at the given point. Note that we've also found the change in y along the tangent line corresponding to `dt = .4.
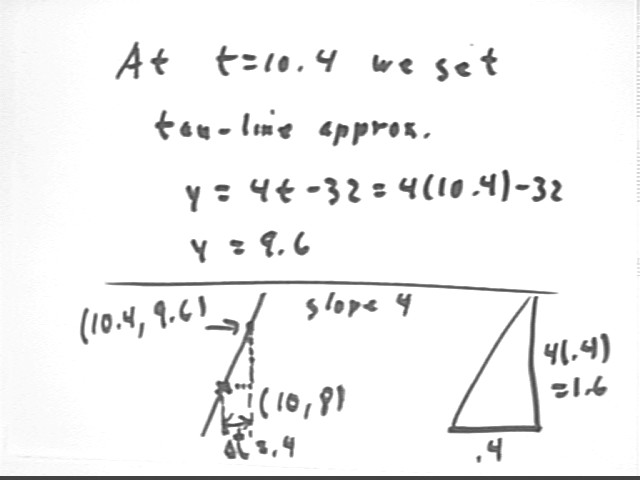
We compare our tangent-line approximation with the actual value of y:

EXTENDING THE EXAMPLE:
We observe that our tangent-line function underestimated the change in y. This will be the case if the slope of the y vs. t curve is increasing. If the slope of y vs. t is decreasing then the tangent-line approximation will be an underestimate.
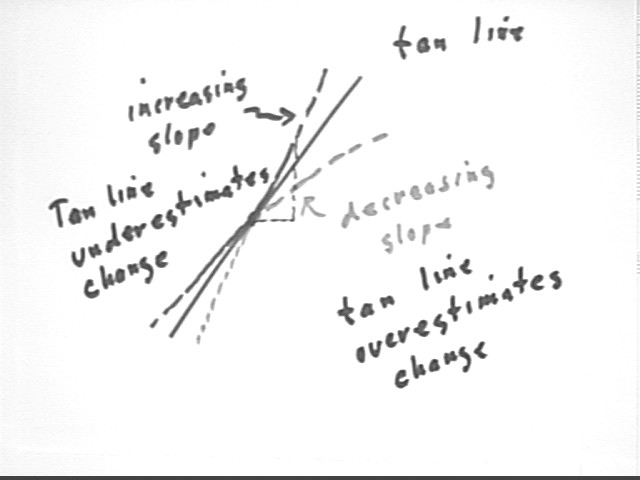
How could we have predicted whether our estimate would be high or low?
The behavior of the slope of y vs. t is the key, as we saw in the preceding picture. To see whether the slope is increasing or decreasing we look at the y ' (t) function, which represents the slope, to see whether it is increasing or decreasing.
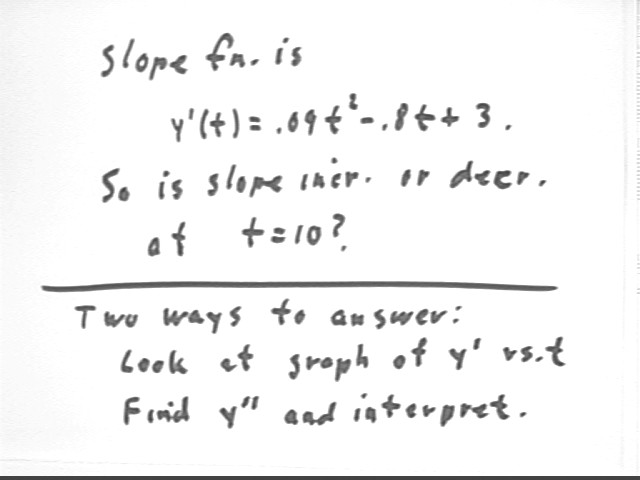
There are two ways in which we might do this.
We might look at a graph of y ' (t) vs. t. If the graph is increasing then the slope of the y vs. t graph is increasing.
We might instead look at the derivative of y ' (t). If the derivative of y ' (t) is positive then y ' (t) is increasing, and if the derivative of y ' (t) is negative then y ' (t) is decreasing.
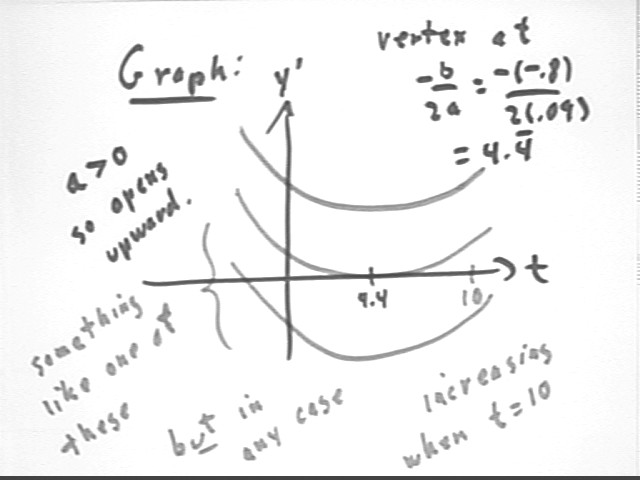
The slope function is a quadratic function so we easily obtain the t value of its vertex. We also see that since the coefficient of t^2 is positive the graph will open upward.
Since t = 10 is to the right of the vertex of an upward-opening parabola, the function will be increasing at t = 10. It doesn't matter what the value of the function is at the vertex (note that 3 possible parabolas with the same vertex are shown below and that the slope at t = 10 is (or should be) the same for each).
We conclude that y ' is increasing at t = 10, telling us that the slope of the y vs. t graph is increasing at t = 10 and confirming that the tan-line approximation should be an underestimate.
We can alternatively see that the derivative y '' (t) of the y ' (t) function is positive when t = 10. This tells us that the y ' (t) function is increasing when t = 10 and leads to the same conclusion reached by looking at the graph.
Note that the calculation here is probably easier and less error-prone than constructing the graph. However doing it both ways leads to deeper insight as well as a good check of the result.
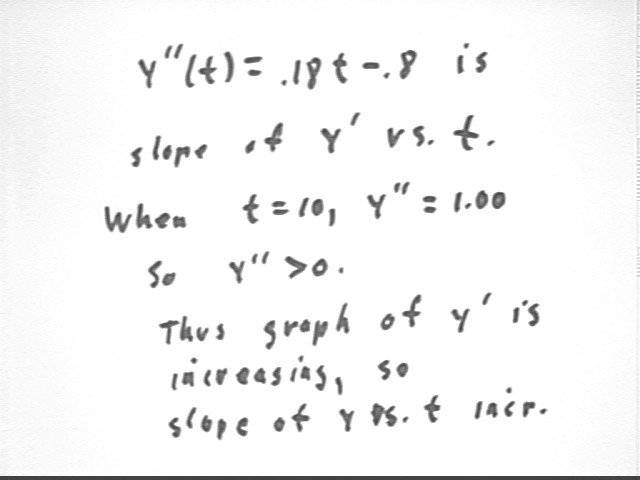
2. If we know that y ' (t) = -.08 * sqrt( y(t) ) then if at clock time t = 0 we have y ( t ) = 100, what is y ' (t) at t = 0?
If y(t) = 100 then y ' (t) = -.08 sqrt(y(t) ) = -.08 sqrt(100) = -.8.
Interpretation in terms of flow model: When depth is 100 cm the rate of depth change is -0.8 cm / s.
If y ' (t) does not change appreciably between t = 0 and t = 10, what then will be the approximate value of y at t = 10?
If y ' (t) stays at -.8, which is effectively will if it doesn't change appreciably, then the change of y between t = 0 and t = 10 will be `dy = y ' * `dt = -.8 * 10 = -8.
Thus y will change from 100 to 100 + `dy = 100 - 8 = 92.
Interpretation: The depth continues to change at -.8 cm/s for 10 sec, changing depth by -8 cm from 100 cm to 92 cm.
The figure below shows this process graphically. The y vs. t tangent-line approximation at t = 0 goes through the point (0, 100) and has slope -.8. We could get the equation of the tangent line and plug in t = 10 to find that at t = 10 we have y = 92. In the figure below this is shown by simply calculating the `dy corresponding to y ' = -8 and `dt = 10.
The figure also indicates how we will find the t = 20 estimate based on the rate of change at the t = 10 depth.
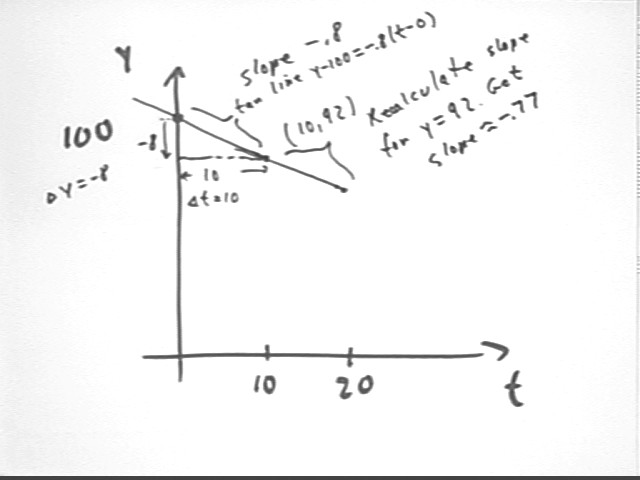
At this new depth what is y ' (t)?
As we saw the depth was y(10) = 92. We can plug this back into the formula for y ' (t), obtaining y ' (10) = -.8 sqrt( y(10) ) = -.77, approx..
If y ' (t) does not change appreciably between t = 10 and t = 20, what then will be the approximate value of y at t = 20?
We now obtain a new approximate tangent line through (10, 92) and having slope -.77. Either by finding the equation of the tangent line and plugging in t = 20, or by directly calculating `dy = y ' (t) * `dt we will find that the depth at t = 20 is approximately 84.3.

The process we saw in the above is summarized in the diagram below. Having the information to calculate the initial y ' we use the given `dt to find the change in y and hence the new y. Then we get the new values of y and of t, which we then plug back into our calculation for y ' to begin the next step. This process can be continued indefinitely.
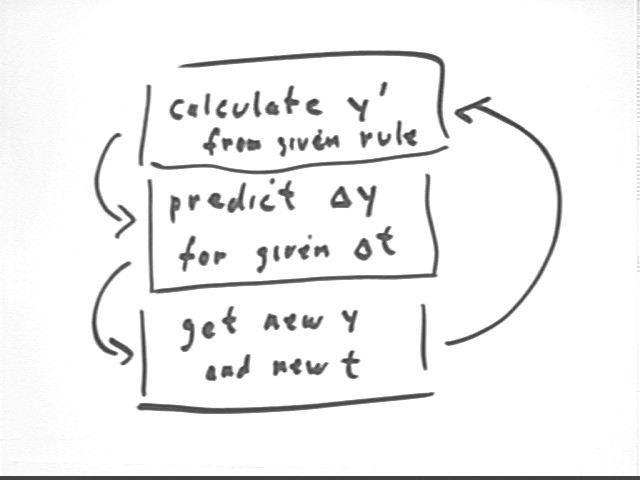
Note however that the assumption that y ' doesn't change significantly over the time interval isn't completely correct; in general it does change a little bit and gradually at first, then more and more rapidly with each new estimate, the errors that result from our not-quite-correct assumption will build up and eventually render our approximation useless.
To solve the equation 4 * 3^x = 7 * 5^x we use the laws of logarithms and basic algebra to find x.
We first take the natural log of both sides, then apply the law log(A * B) = log(A) + log(B), then apply the law log(b^x) = x log b.
We then collect x terms on the left-hand side, factor out x and divide by the factor of x.
We can use a calculator to approximate the final result.
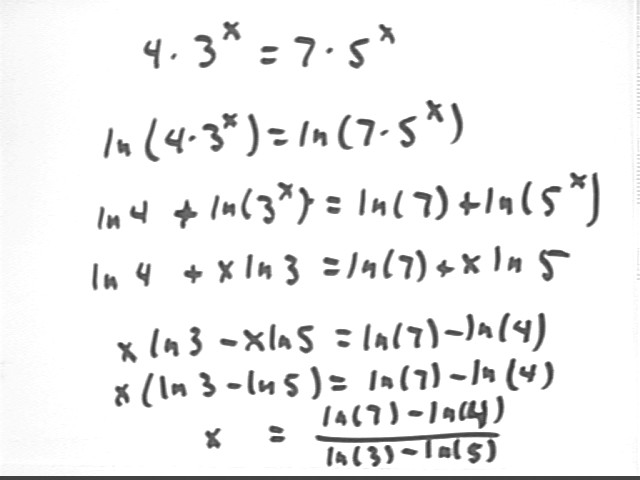
Note that had we used log instead of ln our steps would have been identical, except that we would have log where the above reads ln. The final result comes out the same whether we use log or ln.
Note also that the last line could be written x = ln(7/4) / ln(3/5).