Calculus I Quiz 0916
Given that y ' (t) = -.02 sqrt(y(t)) * (t / 10) and the knowledge that at t = 0 we have y = 100, use an interval `dt = 10 to estimate y(t) at t = 10, t = 20 and t = 30.
We calculate y ' based on y and t at every successive point, and assume that y ' doesn't change over the next `dt increment. We thus predict the approximate y after the `dt increment.
We iterate this process until we get y at the desired t.
The shorter the interval `dt the more work we have to do to get where we want to go, but the more accurate our approximation will be, since y ' will change much less over a short increment than a large one.
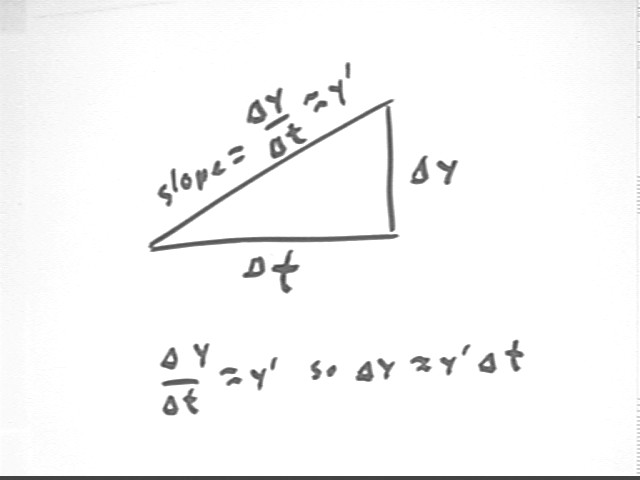
Note that from the 'slope triangle' and the fact that y ' the approximate average slope we know that `dy = y ' * `dt.

First Step
At t = 0 and y = 100 we get y ' (t) = 0.
So between t = 0 and t = 10 we have `dy = y ' * `dt = 0.
Thus at t = 10 we have y = 100.

Second Step
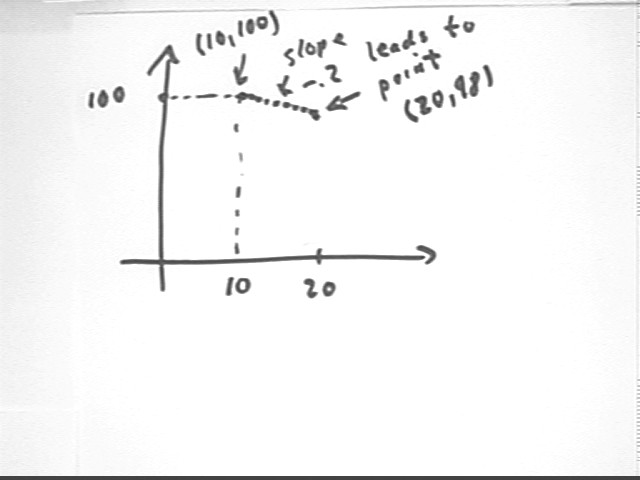
Now when t = 10 and y = 100 we have
So between t = 10 and t = 20 we have
Thus at t = 20 we have y = 100 + -2 = 98.
Third Step
At t = 20 we therefore get y ' (t) = -.02 sqrt(98) * (20/10) = -3.96.
So between t = 20 and t = 30 we get
`dy = y ' `dt = -.396 * 10 = -3.96.
Thus at t = 20 we have y = 98 + -3.96 = 94.04.
Fourth Step
We now have y = 94.04 at t = 30. We use these values to calculate y ' at this point, then assume that y ' doesn't change again until t = 40.
We'll get y ' = -.58 etc.
Do you think your final estimate is higher or lower than the actual value of y at t = 30?
It appears that the slopes are decreasing, so that the average slope over any given interval is probably less than the slope at the beginning of the interval. Since we are using the initial slope on each interval to calculate the change in y, this means that our estimated change is likely greater than the actual change so we are probably overestimating our y values.
Since y changes are negative we are therefore underestimating the decreases.
Solutions to selected text problems
After taking ln of both sides we must recognize in the second step that we have a quadratic equation and arrange it accordingly in the third step:

Remember that ln 7 is just a number, which we will evaluate at the end of the problem if we calculate an approximate value of x. The solution given here is an exact solution:
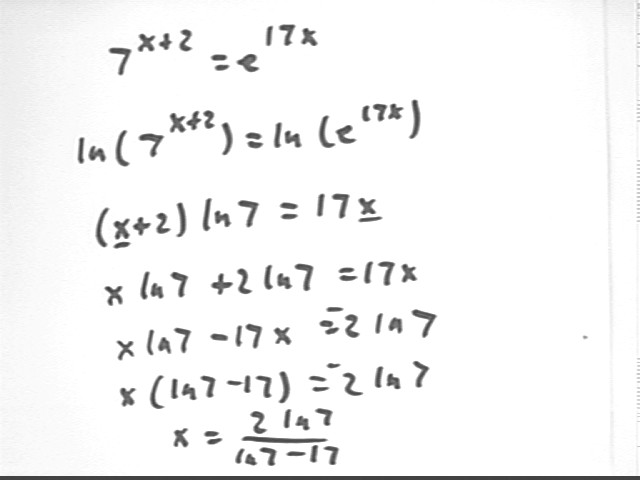
Note how the third step is in the form of a quadratic equation, which is put into standard form in the fourth step.
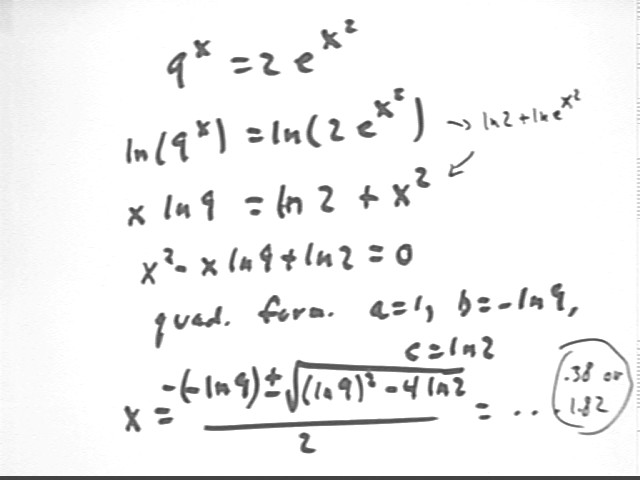
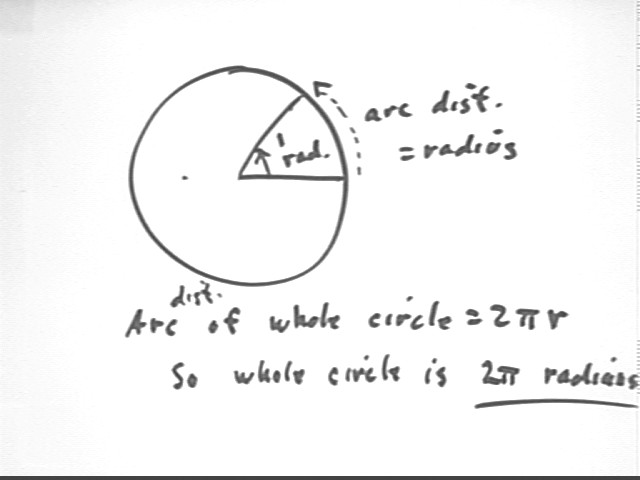
Definition of the radian. Note that we can immediately determine that there are 2 pi radians in a circle.
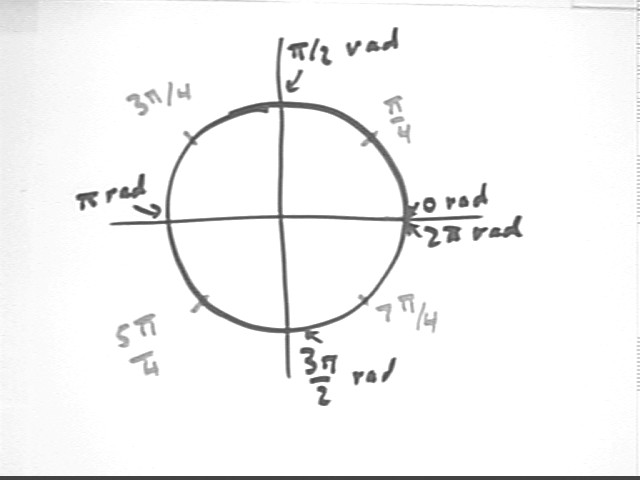
Angular positions on a circle are found by dividing the 2 pi radians of the full circle by 4 to get multiples of pi/2 and by 8 to get multiples of pi/4.
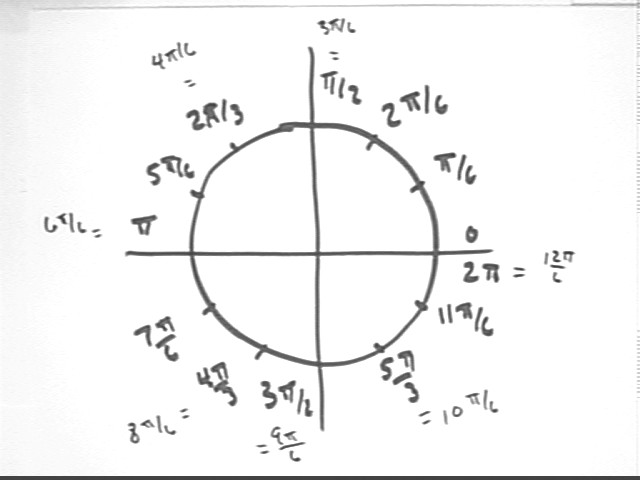
If we divide the angular displacement around the circle into 12 equal parts we get the angular positions which are multiples of pi/6.
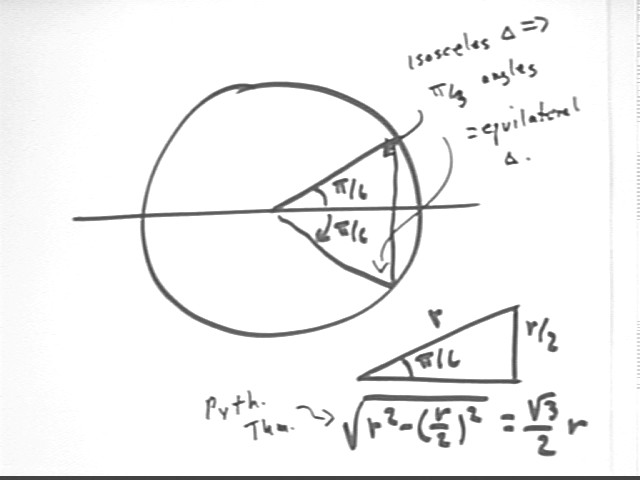
We find the sides of the 'pi/6 triangle' using basic geometry and the Pythagorean Theorem.
Using the circular definitions of the sine and cosine functions we find the sine and cosine of pi/6:
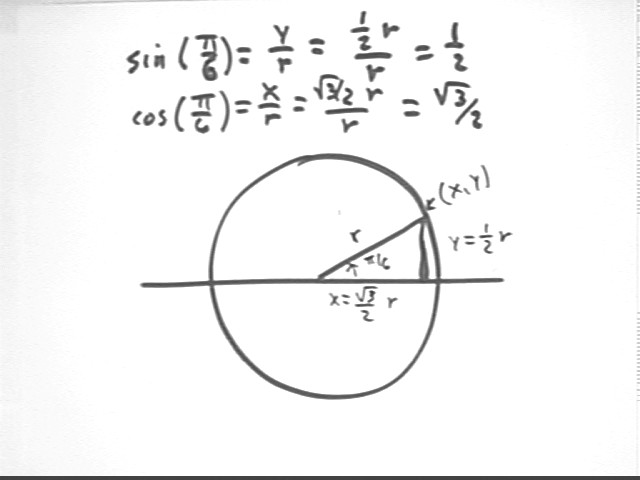
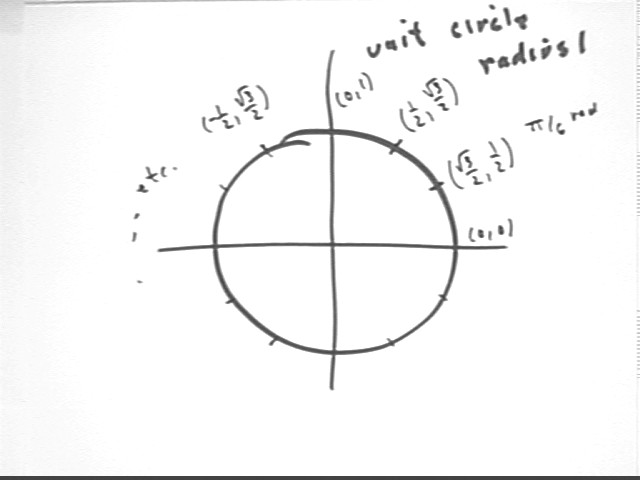
We can now specify the x and y coordinates of every point on the unit circle whose angular position is a multiple of pi/6.
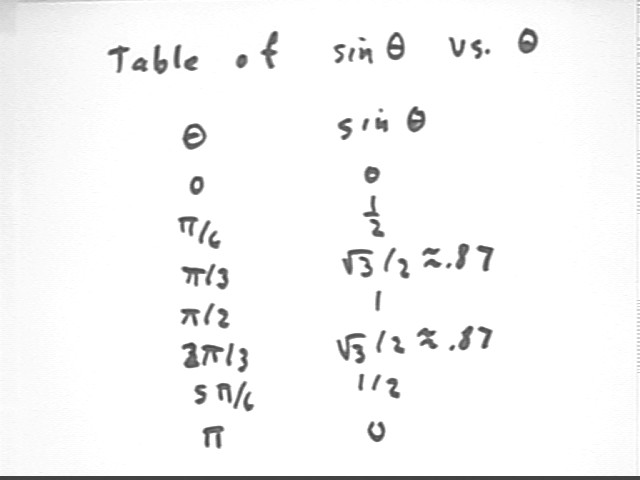
We make a partial table of sin(theta) vs. theta.
We graph our partial table, then referring back to our circle we see how the graph will continue.
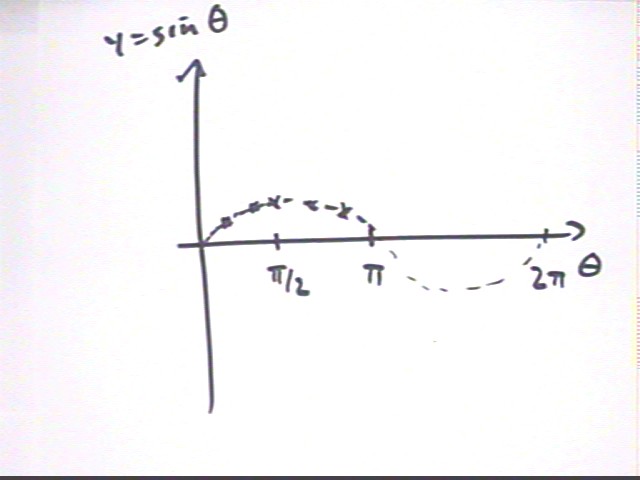
As we go around the circle again and again our angle will go from 0 to 2 pi to 4 pi to 6 pi etc.