Calculus I Quiz 0920
Problem Number 1Problem: The quadratic depth vs. clock time model corresponding to depths of 31.64745 cm, 25.91966 cm and 22.81666 cm at clock times t = 8.786311, 17.57262 and 26.35893 seconds is depth(t) = .017 t2 + -1.1 t + 40.
Problem: The quadratic depth vs. clock time model corresponding to depths of 31.64745 cm, 25.91966 cm and 22.81666 cm at clock times t = 8.786311, 17.57262 and 26.35893 seconds is depth(t) = .017 t2 + -1.1 t + 40.
Problem: Write the differential equation expressing the statement that the rate which the temperature T changes with respect to time t is proportional to the difference between the temperature T and the 27 degree room temperature.
Problem: If dy / dt = 1.13 y^2 + 1.24 y/(t+1), and if at t = 0 we have y = .95, then find the approximate value of y when t = .3. Using the new values of y and t, find approximate value y when t = .6. Continue for two more steps to find the approximate value of y when t = 1.2.
(extra credit): Use a predictor-corrector method, with `Dt = .6 instead of the .3 used above, to find the approximate value of y when t = 1.2. Which value do you think is more accurate?
Problem Number 3Determine the average rate of change of the function y(t) = .3333333 t 2 + -51 t + 86 between t and t + Dt.
What are the growth rate, growth factor and quantity function Q(t) for a radioactive element which initially has 1780 grams if the amount decreases by 6% every week?
Problem Number 4Solve using ratios instead of functional proportionalities:
If a sand pile 3 meters high has a mass of 50000 kg, then what would we expect to be the mass of a geometrically similar sand pile 17 meters high? Using the differential estimate the mass of sand required to increase the height of the pile from 3 meters to 3.001 meters.
Problem Number 6Derive the formula for the derivative of y = a t^3, where a is a constant number.
Average rate of change of y with respect to t is change in y / change in t.
This is the definition of ave rate of change. This is the only definition of ave rate of change.
If we take average rate of change for shorter and shorter time intervals `dt near clock time t, in the limit as `dt -> 0 is the instantaneous rate of change at t.
If we do this for a quadratic function y (t) = a t^2 + b t + c we get y ' (t) = 2 a t + b.
Note that the ave rate of change of y with respect to t between clock times t and t + `dt is [ y(t+`dt) - y(t) ] / `dt. Taking the limit as t -> 0 gives us the expression for y ' (t).
For an exponential function where some quantity y grows at a constant rate r (r is the proportional growth in one time period) we have y = A * b^t, where b is the growth factor 1 + r and A is the initial amount (the t = 0 amount).
Proportionality:
If I have 1 ft x 1 ft x 1 ft cubes, how many does it take to build a solid cube 2 ft on a side?
Gotta build 2 rows of 2 cubes in each row to get one layer, then put another layer on top. Takes 8.
Everyone knows that whales are built up of little cubes. As the whales grow the number of little cubes doesn't change, they just get bigger.
Now if a baby whale is 20 feet long and weighs 6000 lbs then by what factor does its weight change by the time it grows to 40 feet? What will its weight be at the 40 ft length?
Every little whalecube has to double its dimensions, getting twice as long, twice as wide and twice as high. So every little cube attains 2*2*2 = 8 times the volume, and the whale weighs 8 times as much, or 8 * 6000 lbs = 48,000 lbs.
How much will that same whale weigh when it's 60 feet long?
Every little whalecube has to triple its dimensions, getting three times as long, three times as wide and three times as high. So every little cube attains 3*3*3 = 27 times the volume, and the whale weighs 8 times as much, or 27 * 6000 lbs = 162,000 lbs.
How much will that same whale weigh when it's 70 feet long?
The whale has 70/20 = 3.5 times the length, width and height so its weight is 3.5^3 times as much as before, or 6000 lbs * 3.5^3 = ...
Idea:
The weight of a whale is proportional to the cube of its dimensions, assuming geometric similarity at different sizes. We can therefore write
y = k x^3,
where y stands for weight and x for linear dimension.
Or we could write
w = k L^3,
using w for weight and L for length.
So for the given whale we would have
6000 = k * 20^3.
We easily solve for k to get
k = 6000 / 8000 = .75.
Thus w = .75 L^3.
Now if L = 60 we get
w = .75 * 60^3 = ... = 162,000.
We could easily plug in L = 70 or L = 40 to reproduce our other results.
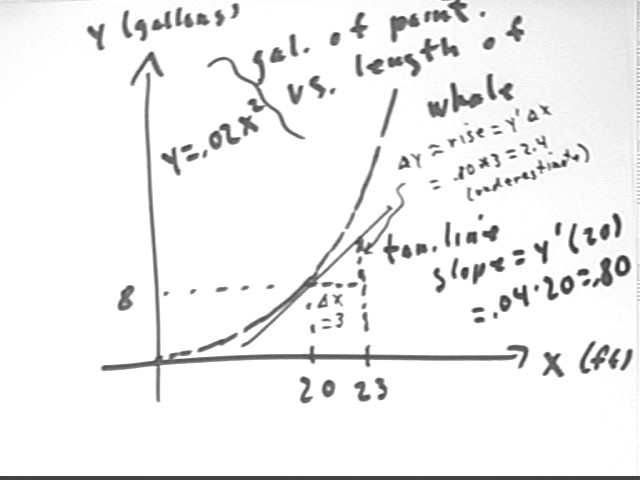
What if we needed 8 gallons of paint to paint the 20 ft whale. How many gallons would be needed for the larger whales?
Whale surfaces are covered by little surface squares, just like any surface. That's why surfaces are said to be 2-dimensional.
So our proportionality for covering whale surfaces is
y = k x^2.
When x = 20 we have y = 8. So
8 = k * 20^2 so
k = 8 / 20^2 = .02.
Thus y = .02 x^2.
We can now plug in x = 40, x = 60 and x = 70 to answer the question.
How much additional paint would be required for a whale 23 feet long?
A graph of y = amt of paint vs. x = whale length shows .02 x^2 vs. x, just a somewhat flattened parabola with vertex at the origin.
At any point x the slope of the tangent line is given by y ' = .04 x.
This is the rate at which y is changing with respect to x.
At x = 20 we have y ' = .04 * 20 = .80. Units are units of rise / units of run = gallons / foot.
We have `dy = y ' * `dx = .80 gal / ft * 3 ft = 2.4 gallons. This approximation assumes that y ' doesn't change, though we know that y ' will be increasing, so this is an underestimate.

To derive the formula for a derivative you have to simplify the expression [ y ' (t + `dt) - y ' (t) ] / `dt and find limiting value as `dt -> 0.