Calculus I Quiz 0930
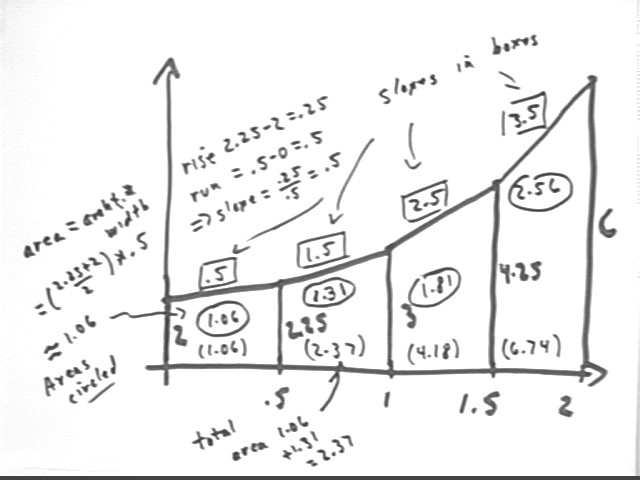
The Trapezoidal Approximation Graph pictured below represents the amount of water in a tank, in hundreds of gallons, vs. the number of hours since the start of a rainy day.
Interpret altitudes, widths, slopes, areas, accumulated areas as appropriate.
Altitudes mean what?
Widths mean what?
Slopes mean what?
Areas mean what?
At what approximate average rate, in gallons / hour, is water accumulating in the tank around t = 1.25 hours?
Slope represents average rate. t = 1.25 hours is in the middle of the third trapezoid, which has slope 2.5, representing 2.5 hundred gallons / hr, meaning that the rate is 250 gallons / hr..
This is only an estimate, but since in this case slopes change linearly with time (slopes on equal intervals are .5, 1.5, 2.5, 3.5) the average slope will indeed be the midpoint slope and 1.25 hours is at the midpoint. So our estimate is in this case exact.
What is the meaning of the number 4.25 on the graph?
We have 4.25 hundred gallons at clock time t = 1.5 hours.
What is the meaning of the number 1.5 on the graph?
The 1.5 on the t axis represents the clock time t = 1.5 hours.
The 1.5 above the second trapezoid represents the average rate of change in amount, in hundreds of gallons per hour, between t = .5 hour and t = 1 hour.
COMMON ERROR: This isn't the change in the amount, it's the rate of change of the amount with respect to clock time.

If the above graph represents the rate, in centimeters per minute, at which the water level in a cylinder is changing, vs. the clock time in minutes then at what rate is the level changing at t = 1.5 minutes?
First do general interpretation. Interpret altitudes, widths, slopes, areas.
Altitudes give rates, in cm/min, at which depth changes.
Widths give time intervals in minutes.
Slopes mean rise / run:
Areas mean ave altitude * width:
Rate of change of depth with respect to clock time is indicated by altitude, so ave rate at t = 1.5 minutes is the corresponding altitude 4.25 cm/minute.
How much change is there in the depth of the water in the container between t = .5 and t = 1 minute?
This is the area of the trapezoid between t = .5 and t = 1, which is 1.31 cm.
How much change is there in the depth of the water in the container between t = .5 and t = 2 minutes?
This will be the sum of the areas of the three trapezoids between t = .5 and t = 2. This sum is 1.31 + 1.81 + 2.56 = 5.68, representing 5.68 cm.
Alternatively, and more appropriately, this is the difference in accumulated areas from t = .5 to t = 2. Accumulated area to t = .5 is 1.06, representing depth change of 1.06 cm since t = 0, and accumulated area to t = 2 is 6.74, representing 6.74 cm depth change since t = 0. The difference is 6.74 - 1.06 = 5.68, representing the depth change of 5.68 cm between t = .5 and t = 2.
What does the number 2.5 represent on this graph?
2.5 represents the average rate at which the rate of depth change changes between t = 1.5 and t = 2, in cm/s/s.
What is a plausible polynomial corresponding to the pictured graph?
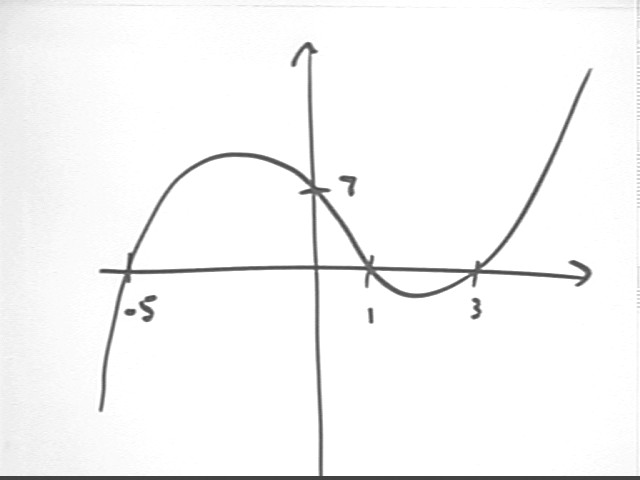
It's a cubic polynomial because it's got 3 zeros. (good answer)
Zeros are at -5, 1, 3. So we conclude that (x - -5), (x - 1) and (x - 3) are factors, since these expressions are respectively zero at the three given points.
From this we conclude that the polynomial is of the form
f(x) = k (x + 5) ( x - 1) ( x - 3).
We see also that the y intercept is 7, so f(0) = k ( 0 + 5) ( 0 - 1) ( 0 - 3) = k * 15, and f(0) = 7. So we have
k * 15 = 7, or k = 7/15 and the polynomial is
y = 7 / 15 ( x + 5) ( x - 1) ( x - 3)
= 7·x^3/15 + 7·x^2/15 - 119·x/15 + 7
with graph
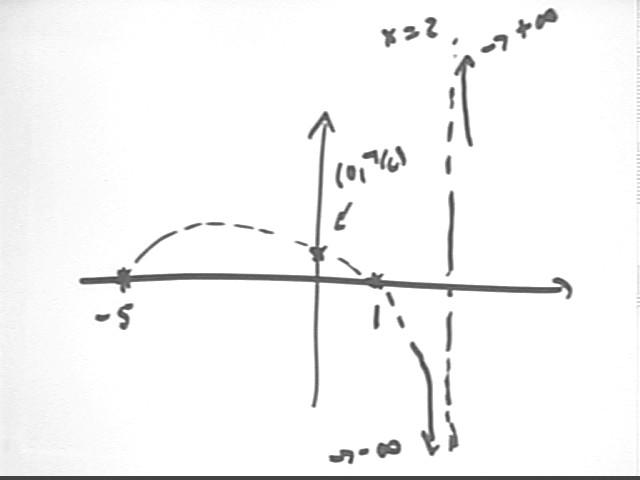
Sketch a graph of [ 7·x^3/15 + 7·x^2/15 - 119·x/15 + 7 ] / (x^2 - 5 x + 6).
In factored form this is 7/15 * ( x+5)(x-1)(x-3) / [ (x-2)(x-3) ].
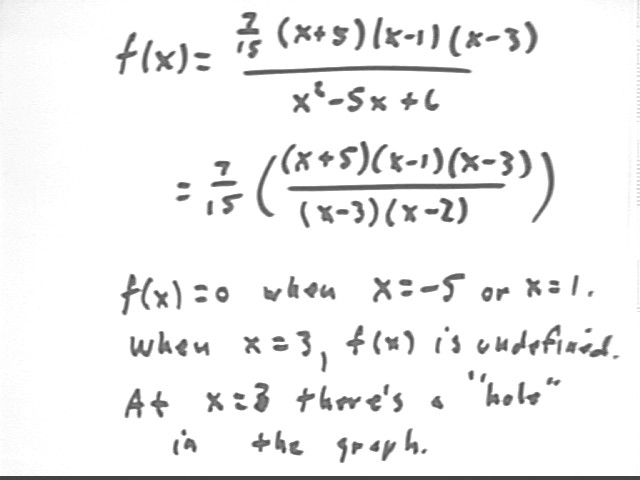
This function is undefined if x = 2 and also if x = 3, since division by 0 is not defined.
Near x = 3 the function behaves like 7/15 * ( x+5)(x-1) / [ (x-2) ]. So except for a 'hole' in the graph where x = 3 the function gives us a smooth graph in this vicinity.
Near x = 2 the function is 7/15 * ( x+5)(x-1) / [ (x-2) ], since near x = 3 we don't have x = 3 and we can divide x-3 by x-3 to simplify the expression.
As x approaches 2 the denominator approaches 0 and the numerator doesn't so the magnitude of the quotient approaches infinity. Note that when x is close to 2 the expression is close to 7/15 * (2+5)* (2-1) / (x-2) = 49 / [ 15 (x-2) ].
Between x=-5 and x=1 there are no zeros so the function is either always positive or always negative on this interval. Since f(0) is positive we conclude that the fn is positive.