Calculus I Quiz 1025
Go across the hall to the computer lab and open DERIVE by clicking on the DERIVE icon on the desktop.
Click in the Expression Box and enter INT(x^2, x, 1, 3). After the expression appears in the big window, click on Simplify, then on Basic. What is your result?
Show the steps of integrating x^2 with respect to x, from x = 1 to x = 3. Remember that the integral is the change in the antiderivative.
Does your result agree with that of the computer?
Integrate f(x) = sqrt(1-x^2) from x = 0 to x = 1 and make note of your result, which you will need in your homework.
Do the same with the following functions:
f(t) = 2.25 * 1.15^t from t = 0 to t = 10, from t = 10 to t = 25, and fro t = 25 to t = 35.
f(t) = 40(1.002)^t from t = 0 to t = 6, from t = 6 to t = 12 and from t = 12 to t = 18.
f(t) = sin(t^2) for t = 0 to t = 1.
Note that these integrals are all relevant to your homework assignment.
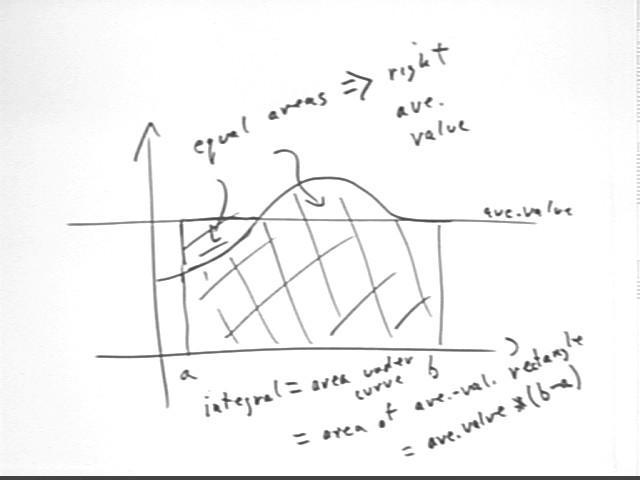
Remember that the average value of a function on an interval can be thought of as integral / interval. You should understand this statement in the context of the two figures below. A similar figure is explained in the preceding set of class notes.


To find the ave val of e^t on the interval (0, 10) we divide the definite integral by the length of the interval. Be sure you understand this process in terms of rate functions and changes in amounts (the change-in-amount function is an antiderivative of the rate function so the change in amount is change in the antiderivative of the rate function).
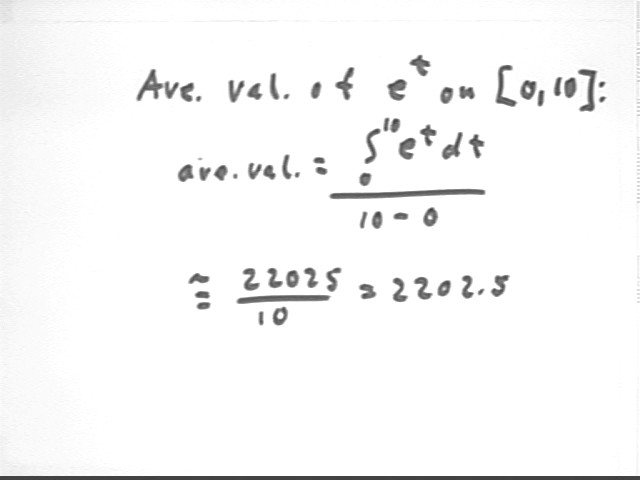
Integral interpretation comes down to the interpretation of the areas of trapezoids. If we know the meaning and units of the ave graph altitude and the graph width we can easily find the units, and hopefully the meaning, of the area, which gives us the meaning of the integral.

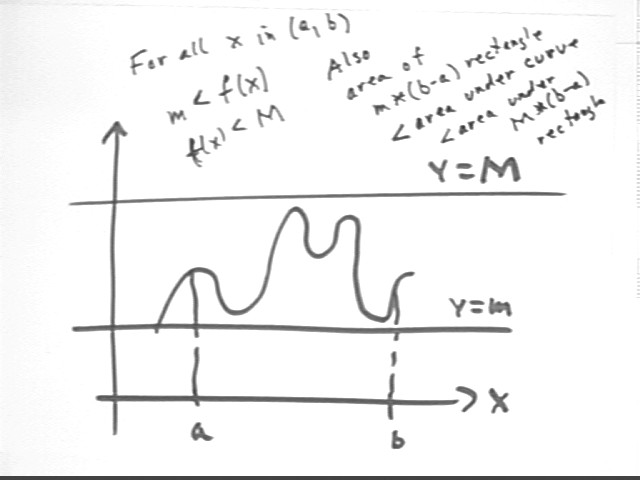
If a function f(x) has the property that on the interval (a, b) the function is bounded below by m (i.e., the function is always greater than m on the interval) and above by M (i.e., the function is always less than M on the interval) then a simple picture demonstrates that on the interval (a, b) the area under the graph of f(x) is greater than the area under the line y = m, and less than the area under the line y = M.
This leads to the Theorem that for f(x), a, b, m and M as specified in the preceding paragraph
m < INT(f(x), x, a, b) < M.