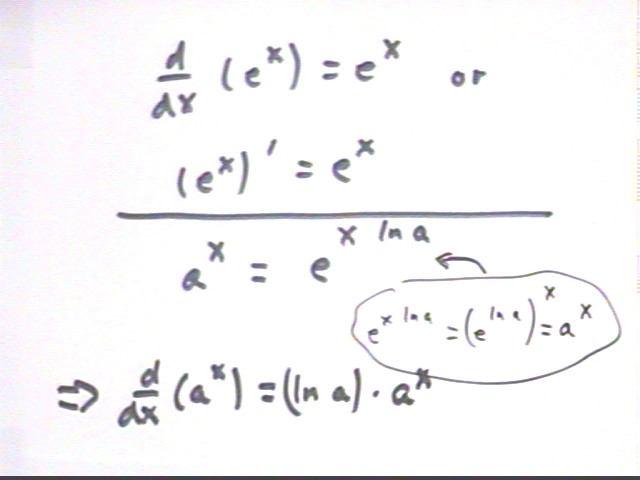
Calculus I Quiz 1101
Problem Number 1Write the differential equation expressing the hypothesis that the rate of change of a population is proportional to the population P.
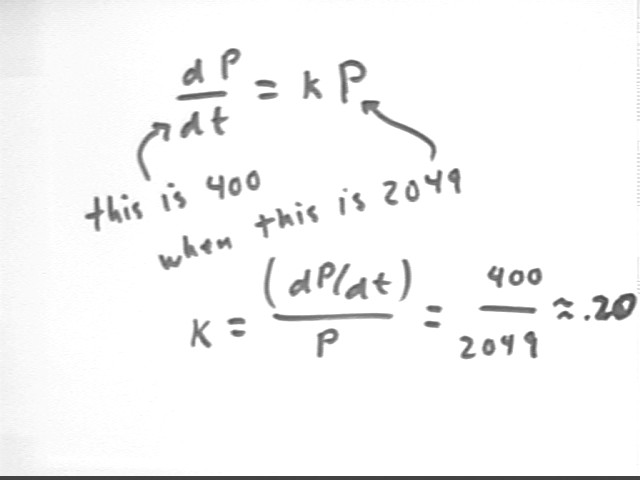
We translate (the rate of change of a population) as P' or, better, as dP/dt.
We translate (is proportional to the population P) as (= k * P for some constant k).
So our statement is
Evaluate the proportionality constant if it is known that the when the population is 2049 its rate of change is known to be 400.
The figure below depicts the proportionality relationship dP/dt = k P in a diagram indicating the given values of dP/dt and P.
k = (dP/dt) / P = 400 / 2049 = .2, approx. so our relationship is dP/dt = .2 P.

If this (i.e., P = 2049 and dP/dt = 400) is the t=0 state of the population, then approximately what will be the population at t = 1.9?
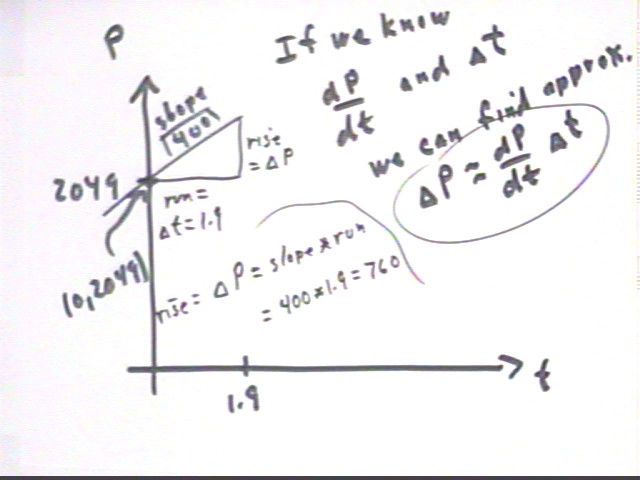
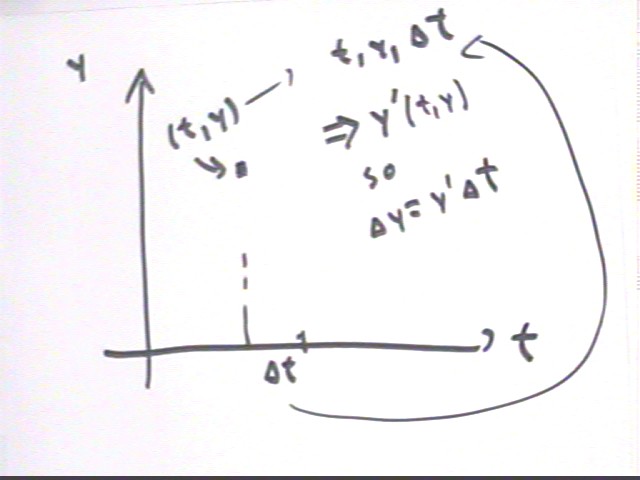
Using the basic rate relationship change in quantity = rate * change in clock time we see that for short time intervals `dt (assuming a smooth function P(t)) we can approximate change in population by `dP = dP/dt * `dt.
Equivalently we see that the given initial population gives us the (0, 2049) point on the graph below and the given initial rate dP/dt = 400 tells us the slope of the graph at the t = 0 instant. Assuming that dP/dt doesn't change much between t = 0 and t = 1.9 we can follow the 'slope line' to obtain an estimate of P at t = 1.9. The corresponding 'slope triangle' has run 1.9 and slope 400 so its rise is `dP = run * slope = 400 * 1.9 = 760. Adding this change in P to the original P we get P = 2809.
What then will be the population at t = 3.8?
Starting from the point (1.9, 2809) predicated by the last calculation we can predict P for t = 3.8.
At (1.9, 2809) we get dP/dt = .2 * P = .2 * 2809 = 562, approx..
This tells us that the graph will have slope 562 at this point. Following that slope from t = 1.9 to t = 3.8 will yield the next value of P.
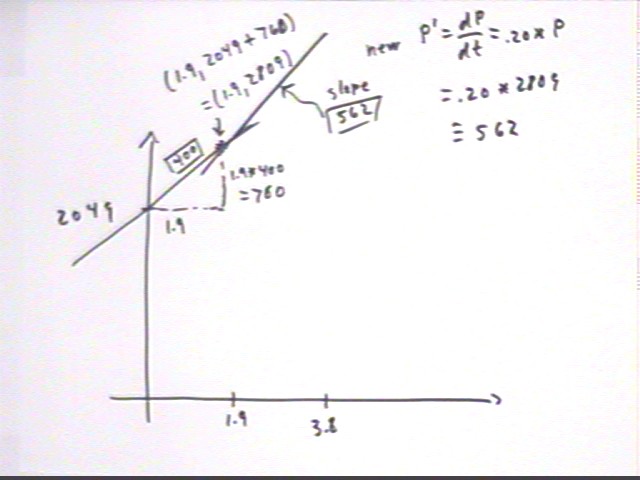
We will get a 'slope triangle' whose run is 3.8 - 1.9 = 1.9 and whose slope is 562, giving us a rise of 562 * 1.9 = 1050, approx.., so that the new value of P will be 2809 + 1050 = 2960 approx..
This corresponds to the following reasoning:
As P = 2809 we have dP/dt = 562, which is the time rate of population change. Multiplying this rate by `dt = 1.9 we obtain `dP = dP/dt * `dt = 1050, approx.. This calculation is an approximation based on the premise that dP/dt doesn't change significantly over the 1.9 sec time interval.
Problem Number 4Problem: Write the differential equation expressing the statement that the rate which the temperature T changes with respect to time t is proportional to the difference between the temperature T and the 28 degree room temperature.
The equation is dT/dt = k ( T - 28).
Problem: If dy / dt = .96 y^2 + 1.15 y/(t+1), and if at t = 0 we have y = .85, then find the approximate value of y when t = .2. Using the new values of y and t, find approximate value y when t = .4. Continue for two more steps to find the approximate value of y when t = .8.
The process is nearly identical to that used in the previous problem. If we know t and y we can find y ' and knowing y ' and `dt we can find `dy.
The derivative of an exponential function
We wish to find the derivative of y = e^x.
We begin by finding the difference quotient and taking its limit as `dx -> 0.
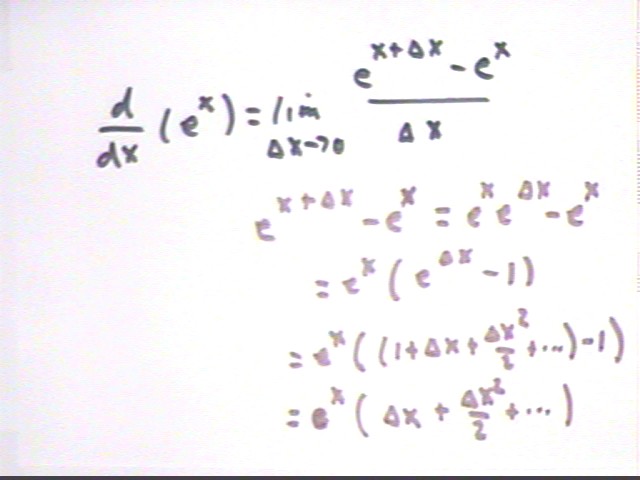
Why e^(x + `dx) is written as e^x * e^`dx.
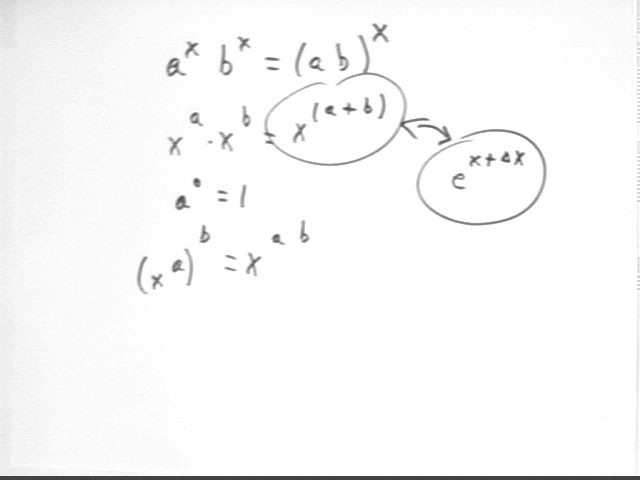
Our simplification of the difference quotient is repeated and extended below. Between the third and fourth line the `dx in the denominator divides into the `dx, `dx^2 and higher powers of `dx, leaving us an expression for which we easily find the limit as `dx -> 0.
The result is that (e^x) ' = d(e^x) / dx = e^x.
The exponential function e^x is its own derivative (and then, obviously, its own antiderivative).
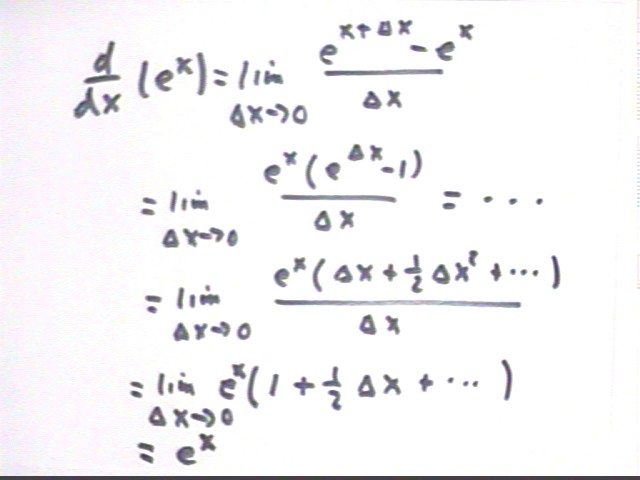
To see why e^`dx = 1 + `dx + `dx^2/2 + ... we first write e in terms of its definition e = lim{n -> infinity} ( (1 + 1/n)^n ).
It follows that e^`dx = lim{n -> infinity} ( (1 + 1/n)^n ) ^ `dx = lim{n -> infinity} ( (1 + 1/n)^ (n * `dx) ).

The Binomial Theorem tells us that (a + b) ^ n = a^n + n a^(n-1) b^1 + n ( n-1) / 2 * a^(n-2) b^2 + ... + b^n.
If we apply this to the expression (1 + 1/n) ^ (n `dx), replacing a by 1, b by 1/n and n by n `dx, we get
1^(n `dx) + n `dx * 1 ^ (n `dx - 1) ( 1/n)^1 + n `dx ( n `dx - 1) * 1^(n `dx - 2) ( 1/n)^2 + ....
All powers of 1 give us 1, and for large enough n we can say that n `dx - 1 is practically equal to n `dx so that our expression becomes
1 + n `dx ( 1/n) + n `dx * n `dx / 2 * ( 1 / n^2) + ..., which simplifies to
1 + `dx + `dx^2 / 2 + ..., where it should be clear that the ... will consist of higher and higher powers of `dx, divided by larger and larger numbers.
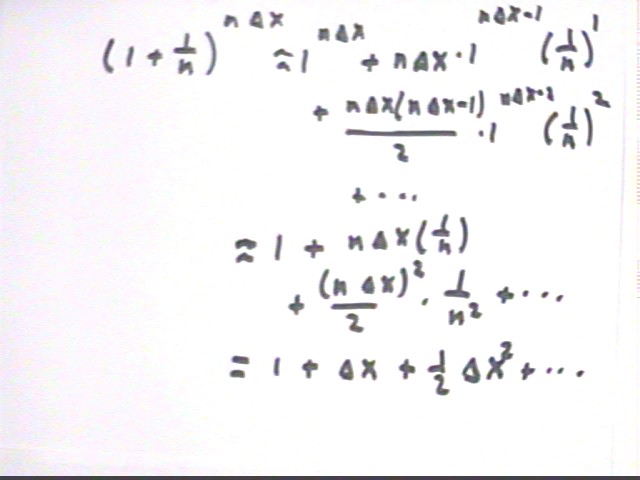
Summarizing we get the expression for e^`dx quoted earlier.
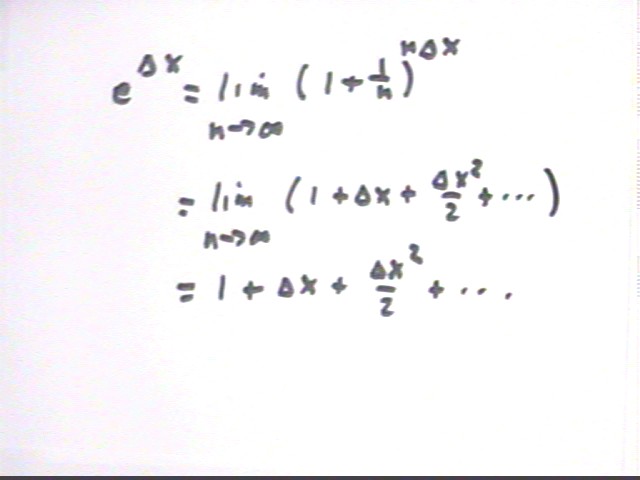
We repeat that the derivative of e^x is e^x, and note in addition that a^x = e^(x ln(a) ).
It will follow shortly from the Chain Rule that the derivative of a^x is ln(a) * a^x.