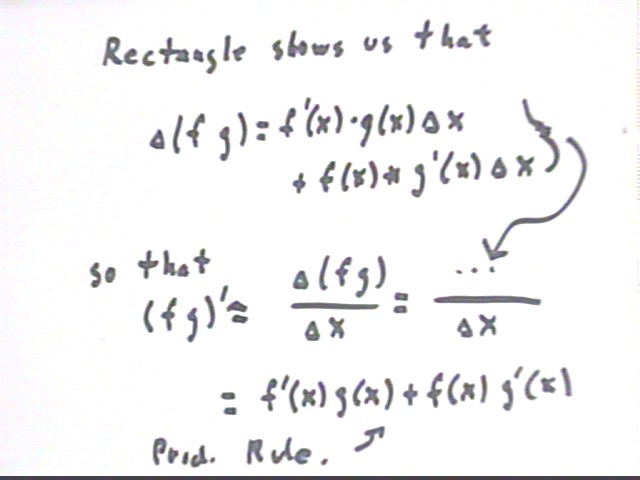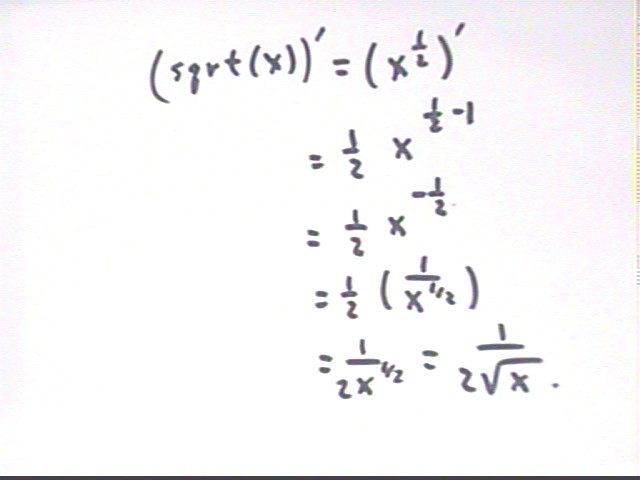
Calculus I Quiz 1104
Find the derivatives of the following:
We convert this to an explicit power function of form y = x^n, obtaining y = sqrt(x) = x^.5. n usually stands for an integer but the rule does extend to non-integer real powers.
Using (x^n) ' = n x^(n-1) we get
(x^.5)' = .5 * x^(.5 - 1) = .5 x^-.5 = .5 / x^.5 = 1 / (2 sqrt(x) ).
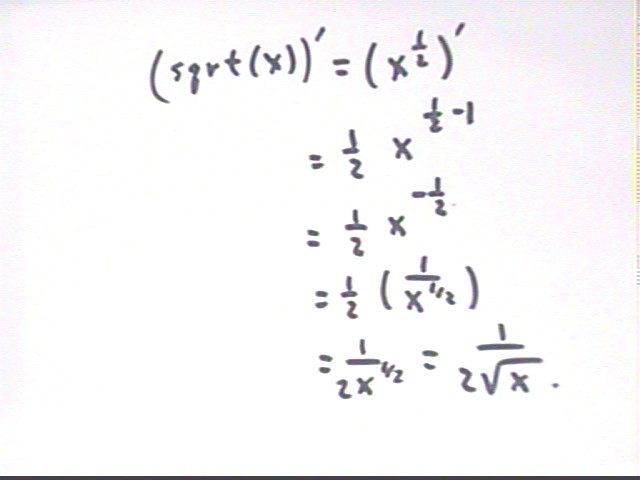
(e^t)' = e^t and for constant c we have (c f(t) ) ' = c f ' (t) so
(4 e^t) ' = 4 (e^t) ' = 4 e^t.
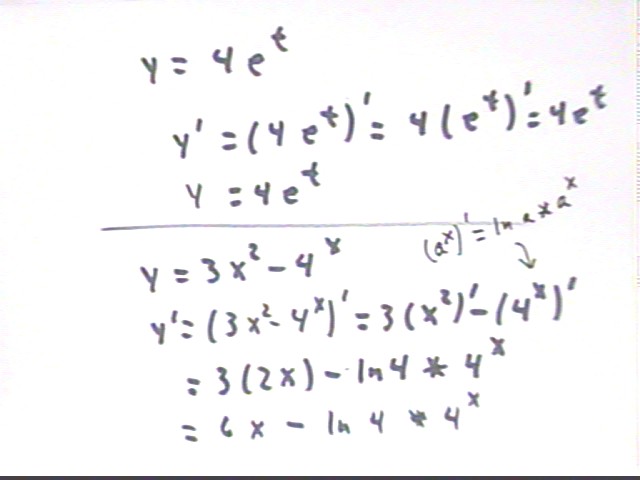
They key here is to convert the function into a power function. sqrt(x) = x^.5 so we get
1/ (x sqrt(x) ) = 1/ (x * x^.5) = 1 / (x^(1 + .5) ) = 1 / x^1.5 = x^(-1.5), better written as x^(-3/2).
This is of the form x^n, and (x^n)' = n x^(n-1) with n = -3/2 so we have
(x^(-3/2)) ' = -3/2 * x^(-3/2-1) = -3/2 x^(-5/2) or if we prefer -3/ (2 x^(5/2) ).
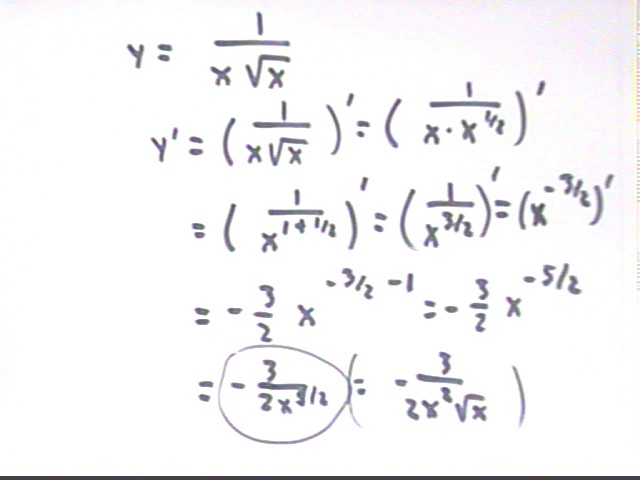
The solution is indicated in the lower half of the figure below.
The derivative is y ' = ( 3 x^2 - 4^x) ' = (3 x^2) ' - (4^x) ' = 3 ( x^2) ' - (4^x) '.
Using the power-function rule for x^2 and the exponential-function rule for 4^x we get
y ' = 6 x - ln(4) * 4^x.
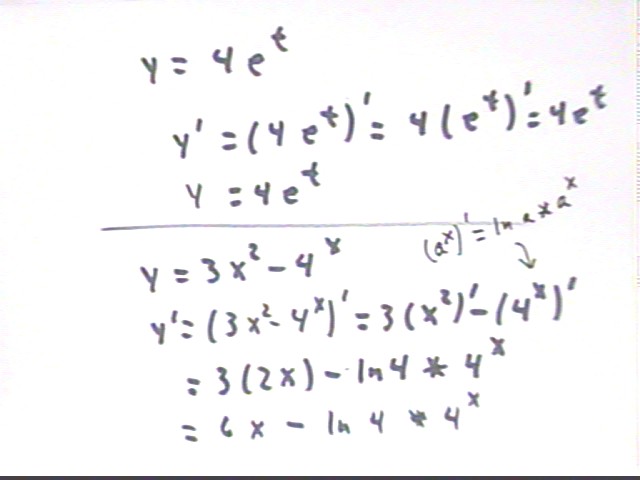
Using the definition of the derivative prove that the derivative of f(x) + g(x) is equal to f ' (x) + g ' (x) .
We apply the limit definition of the derivative to the function (f(x) + g(x)), which gives us the first expression with numerator ( f(x+`dx) + g(x + `dx) ) - (f(x) + g(x)).
This numerator is easily rearranged to the form
f(x+`dx) - f(x) + g(x + `dx) ) - g(x).

This allows us to 'split' the limit into two parts, one of which is the definition of f ' (x) and the other the definition of g ' (x).
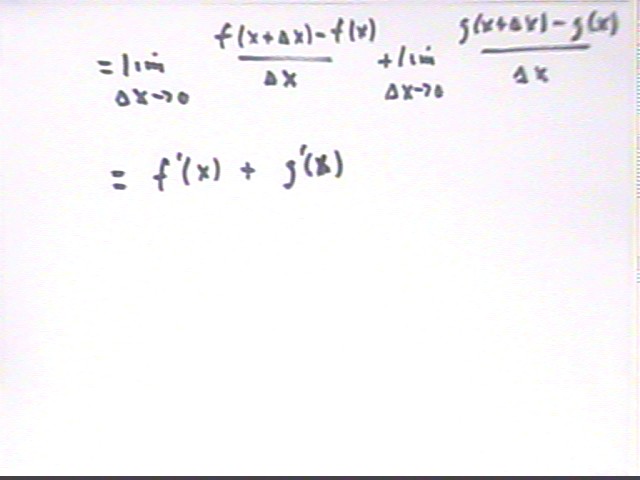
Derivatives of sines and cosines:
The derivatives are
(sin(x)) ' = cos(x)
(cos(x))' = -sin(x).
Details of the derivation of those formulas will be given later. The rules are given here so we can better illustrate the product and quotient rules, and later the Chain Rule.
Product Rule
The derivative of a product function y = f g is
y ' = (f g) ' = f ' g + g' f.
Example: y = x^2 e^x. What is y ' ?
We see that y is a product of the functions x^2 and e^x. That is, y = f g with f(x) = x^2 and g(x) = e^x.
For this f(x) and g(x) we have f ' (x) = (x^2) ' = 2 x and g ' (x) = (e^x) ' = e^x.
So (f g) ' = f ' g + f g' = 2x * e^x + x^2 * e^x = (2x + x^2) * e^x.
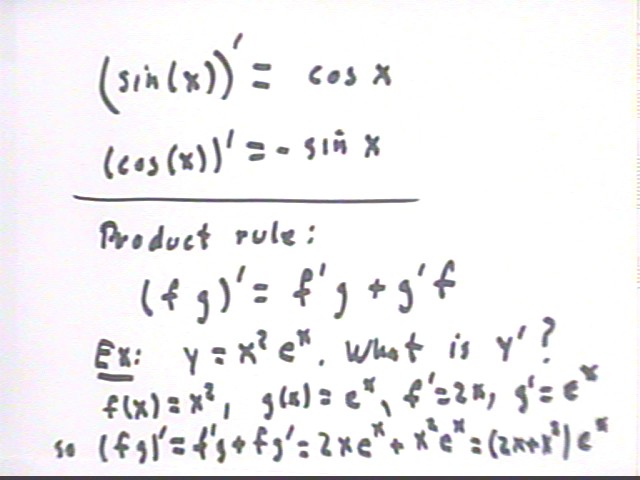
Example: y = e^x sin(x). Find y ' .
This function is also of the form y = f g, this time with f(x) = e^x and g(x) = sin(x).
This gives us f ' (x) = (e^x) ' = e^x and g ' (x) = (sin(x)) ' = cos(x).
Thus y ' = (f g) ' = f ' g + f g ' = e^x sin x + e^x cos x = e^x( sin x + cos x).
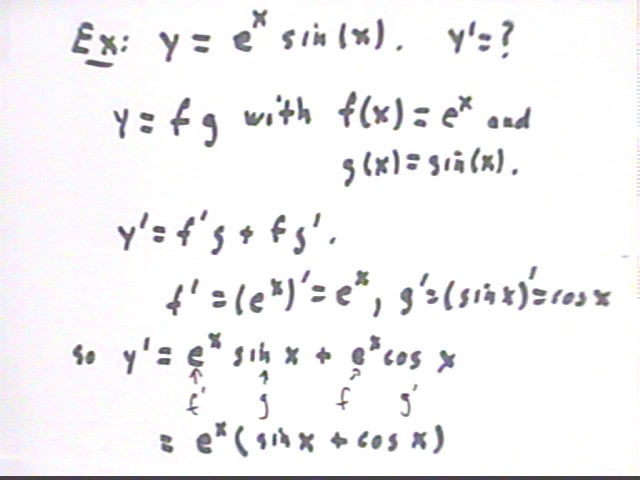
Quotient Rule
The quotient rule says that if y = ( f / g) then y ' = (f / g) ' = ( f ' g - f g ' ) / g^2.
Applying this to y = x^2 / cos(x) we see that y is of the form f / g with f(x) = x^2 and g(x) = cos(x).
Thus f ' (x) = (x^2) ' = 2x and g ' (x) = (cos(x)) ' = sin(x) and
y ' = (f / g) ' = ( f ' g - f g ' ) / g^2 = ( 2 x cos(x) - x^2 (-sin(x)) ) / (cos(x))^2 = x ( 2 cos(x) + x sin(x) ) / cos^2(x).
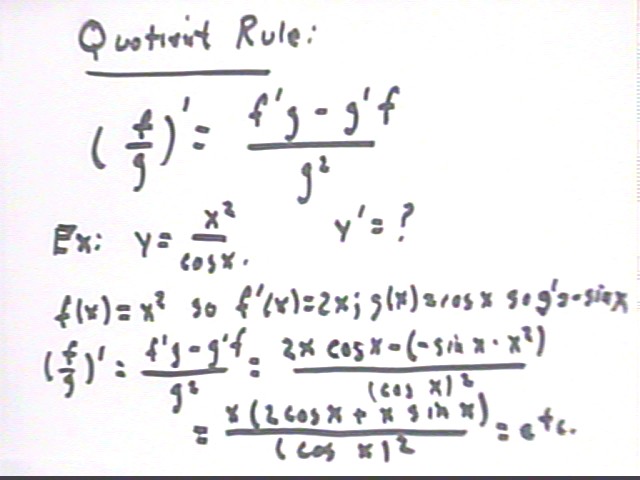
Suppose we have a rectangle with length L and height H. If we increase length by 2% and height by 3%, by what percent does the area change?
The area of the original rectangle is L * H.
The new rectangle has dimensions 1.02 * L and 1.03 * H.
So the area of the new rectangle is 1.02 * L * 1.03 * H = 1.0506 L * H.
This is 1.0506 times the original area L * H. Thus we see that area increases by 5.06 %.
In the preceding example if we increase L by factor a and height by factor b, by what factor does area change?
Again initial area is L * H.
Change in length is a * L so new length is L + a * L = L ( 1 + a).
Similarly the new height is H (1 + b).
So new area is L * H ( 1 + a) ( 1 + b) = L * H (1 + a + b + ab), telling us that area changes by factor a + b + ab.
If a and b are small then ab is really small and we get new area approximately equal to L * H ( 1 + (a + b) ), which tells us that area increases by approximate factor a + b.
If the length of a rectangle is a function L(t) and the height is a function H(t) then if L(t) changes by 2% and H(t) by 3%, by what factor does L * H change?
L * H will change by factor .0506, as seen in a previous example.
If the length of a rectangle is a function L(t) and the height is a function H(t) then if L(t) changes by proportion a and H(t) by proportion b, by how much does L * H change?
L * H will change by factor a + b + ab, as seen in a previous example. If a and b are small enough ab can be neglected and the proportional change is a + b.
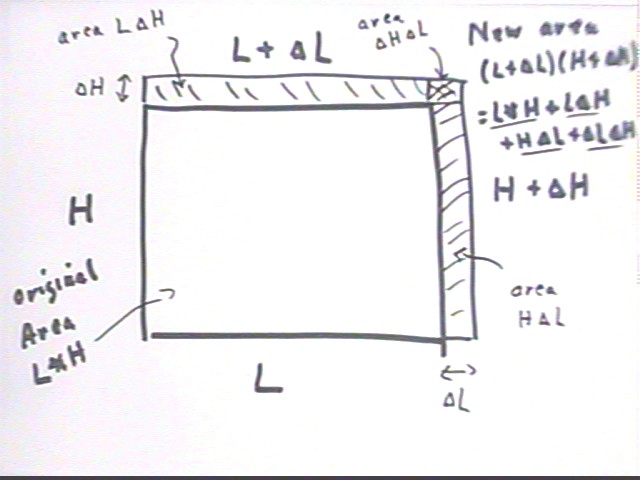
If L changes by `dL and H changes by `dH then by what proportion does the area change?
The new area will be (L + `dL) ( H + `dH) = L H + L `dH + H `dL + `dL * `dH.
The figure below illustrates this. It shows how the changes `dH and `dL affect the area of the rectangle.
These four rectangles have total area L H + L `dH + H `dL + `dL * `dH, in agreement with (L + `dL) ( H + `dH) = L H + L `dH + H `dL + `dL * `dH.
This picture shows us why the change in L * H involves both L * `dH and H * `dL, and also why if `dL and `dH are small enough the 'rest' of the change `dL * `dH is negligible.
Thus `d( L * H ) = L `dH + H `dL, approximately, with the approximation as close as we like if `dL and `dH are small enough.
This is a geometrical interpretation of why the product rule ( f g ) ' = f ' g + f g'.
By the product rule what is the derivative of L * H, where both L and H are regarded as functions of a variable x? By approximately how much does L * H change in a short interval `dx?
The derivative is (L * H) ' = L' * H + H' * L.
In short time interval `dx the change in L * H is approximately (L * H) ' * `dx. We can write this as
(L ' * H + H' * L) * `dx = H * (L' `dx) + L * (H' `dx).
If f and g are functions of x, the figure below represents the product f g as the area of a rectangle with dimensions f by g.
If x changes by `dx then f changes by approximate amount f ' (x) `dx and g by approximate amount g ' (x) dx.
The change in f g is therefore f ' (x) `dx * g(x) + g ' (x) `dx * f(x) + `dx * `dx.
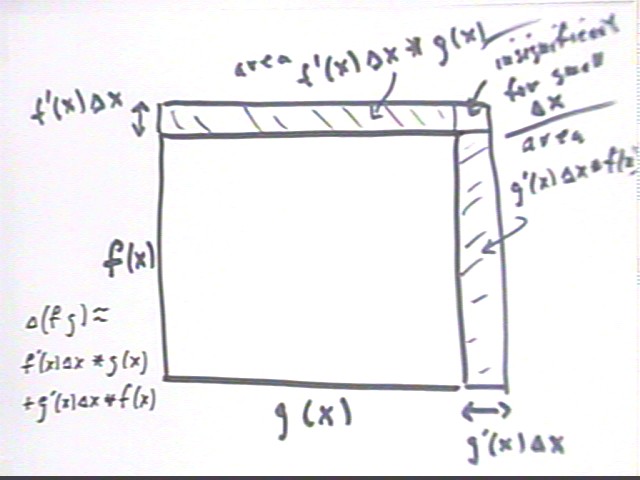
It follows that (f g) ' = lim{`dx -> 0) (`d (f g) / `dx )=
lim{`dx -> 0) ([ f ' (x) `dx * g(x) + g ' (x) `dx * f(x) + `dx * `dx ] / `dx ) =
lim{`dx -> 0) (f ' (x) g(x) + g ' (x) * f(x) + `dx) =
f ' (x) g(x) + g ' (x) f(x), or in short
(f g) ' = f ' g + g ' f.