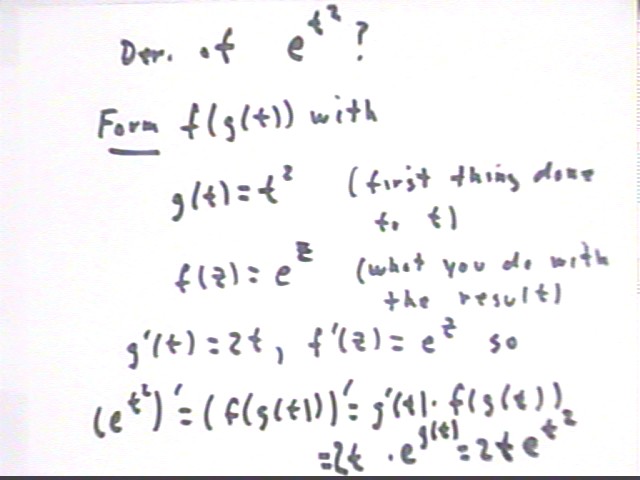Calculus I Quiz 1106
Find the derivatives of the following:
y = sin(t) * cos(t)
The form is y = f g.
The product rule tells us that
y ' = f ' g + f g' = (sin t)' * cos t + sin t * (cos t) ' = cos t * cos t + sin t * (- sin t) = cos^2 t - sin^2 t.

y = x^4 cos(x)
By the product rule
y ' = (x^4) ' * cos(x) + x^4 * (cos(x)) ' = 4 x^3 cos(x) + x^4 * (- sin(x) ) = x^3 ( 4 cos(x) - x sin(x) ).
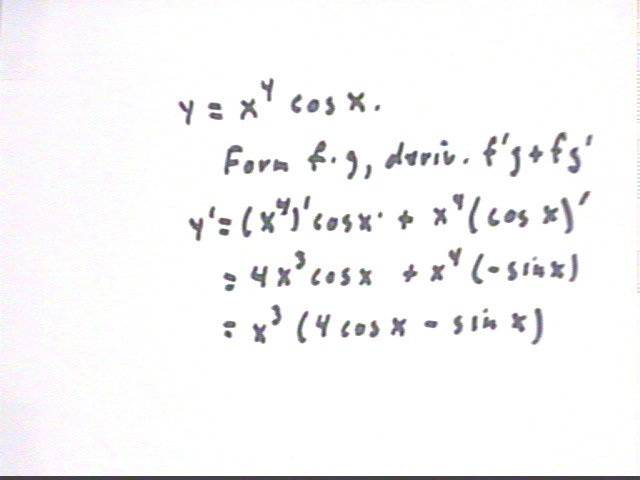
y = x^2 / e^x
By the quotient rule we have
y ' = ( (x^2)' e^x - x^2 ( e^x) ' ) / (e^x)^2 =
( 2 x e^x - x^2 e^x ) / (e^x)^2 =
x e^x ( 2 - x) / (e^x)^2 =
x ( 2 - x) / e^x.
note that the final solution given below isn't completely simplified; if we factor x out of the numerator we get an expression that agrees with the preceding line.
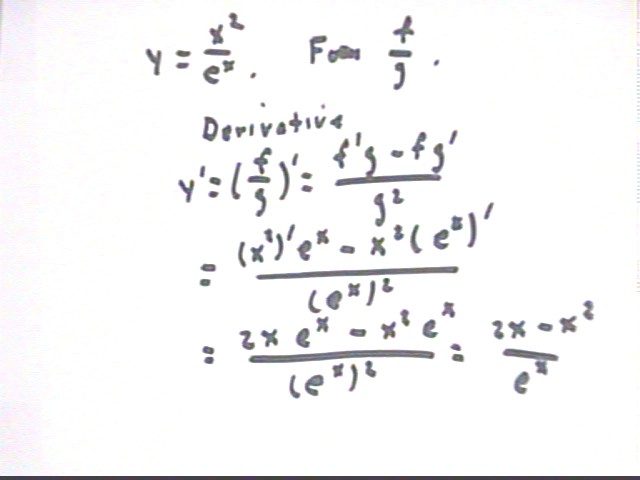
y = sin(t) / cos(t)
By the quotient rule we get
y ' = [ ( sin t ) ' cos(t) - sin(t) ( cos(t) ) ' ] / (cos(t)) ^ 2 =
( cos(t) * cos(t) - sin(t) ( -sin(t)) ) / cos^2(t) =
cos^2(t) + sin^2(t) ) / cos^2 ( t) =
1 / cos^2(t) =
sec^2(t).

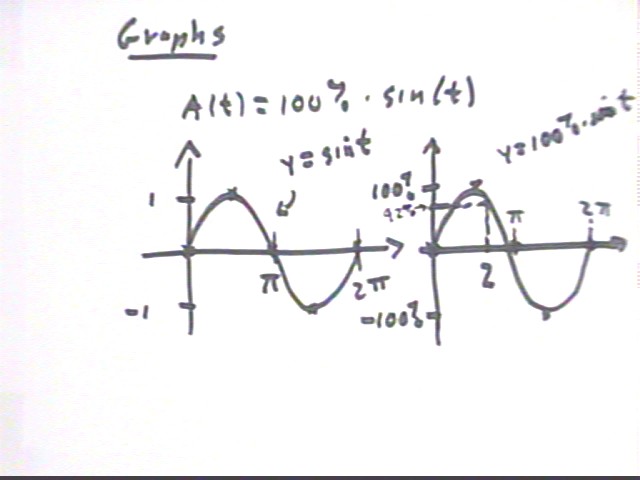
The mental alertness of a typical calculus student during a 3-month term is given by the function A(t) = 100 % * sin(t), where t is clock time in months.
We plug 2 into the expression for A(t) and obtain A(2) = 92%.
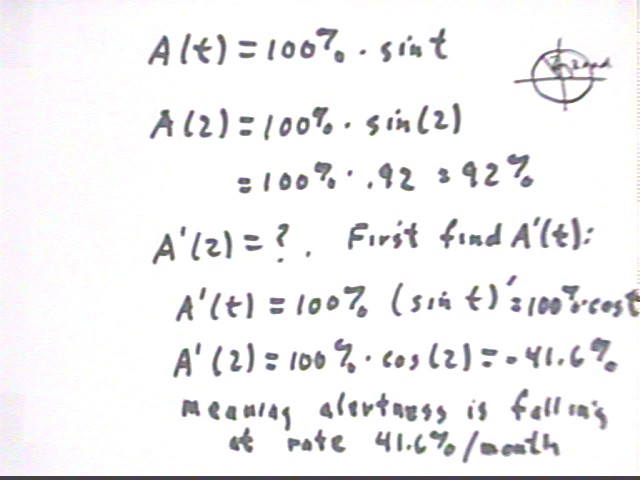
As shown in the preceding figure we first calculate A ' (t), obtaining A ' (t) = 100% cos(t).
Knowing that the derivative represents the rate of change of A with respect to t we know that the units of the derivative must be units of A(t) / units of t, or % / month. So we modify A ' (t) to get the form:
A ' (t) = 100 % / month * cos(t).
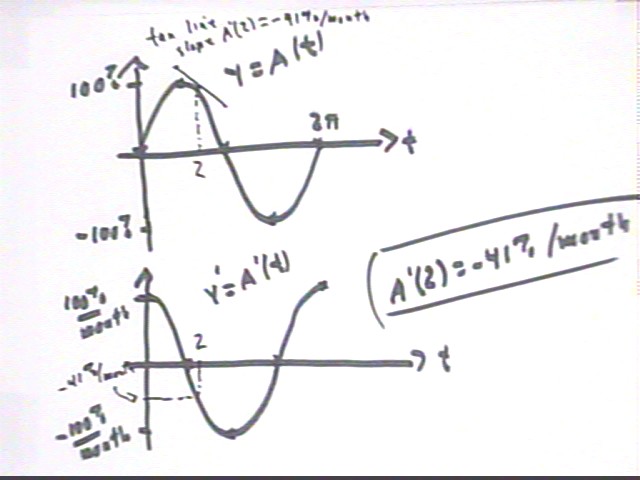
Thus A ' (2) = 100 % / month * cos(2) = 100% / month * (-.41) = -41% / month.
To understand the functions A(t) and A ' (t) we should construct a series of graphs.
The graph of A(t) is easily constructed by considering the reference-circle picture in which sin(t) is the y coordinate of a point moving counterclockwise around the unit reference circle is such a way that the angle with the positive x axis is t. Angle t = 0 places us on the x axis so y = 0; angle t = pi/2 places us on the positive y axis so y = 1; angles t = pi, 3 pi/2 and 2 pi similarly give us y = 0, y = -1 and y = 0. The graph is as indicated in the figure below; note that its amplitude is 1.
The function y = 100% sin(t) will have the same shape but will have amplitude 100%.
The right-hand graph also indicates the t = 2 point, and the fact that A(2) = 92%.
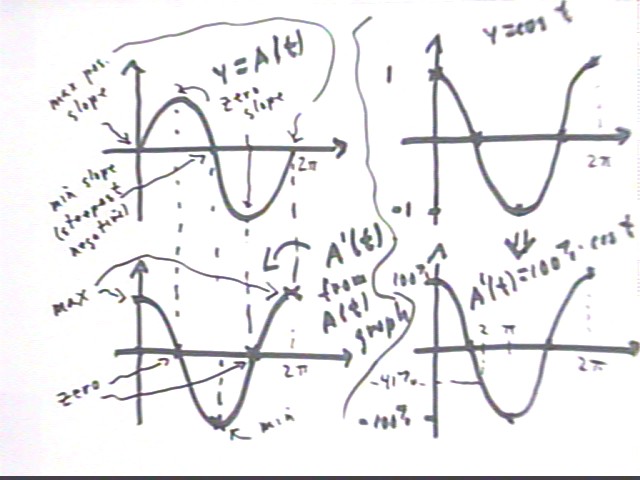
Starting with the graph of y = A(t) (upper left in the figure below) construct a graph of A ' (t).
We note that slope of the A(t) graph represents the value of A ' (t). The slope of the A(t) graph starts with its maximum positive value and decreases to 0 at t = pi/2, then continues to decrease through negative values to its minimum value at t = pi, the increases through negative values to 0 at t = 3 pi/2 and finally returns to its maximum positive value at t = 2 pi. This behavior is indicated in the graph at lower left.
This process is a graphical construction of the derivative and is very important to our understanding of the derivative.
We can also sketch the graph of the derivative function A ' (t) = 100% / month * cos(t). We begin at upper right with a graph of y = cos(t), which is easily constructed in terms of the reference-circle picture.
We then multiply cos(t) by 100% / month (mislabeled on the graph at lower right as 100%). This is indicated by simply relabeling the graph at upper right to reflect the new amplitude. This graph agrees qualitatively with the graph we constructed at lower left, but includes the accurate amplitude, which cannot generally be determined by graphing.
The graph of A(t) can only peak at a point where it levels off--i.e., where its slope is zero. This can occur only if A ' (t) = 0. Note that A ' (t) = 0 at t = pi/2 and at t = 3 pi / 2. At t = pi/2 the graph of A(t) does peak; and at t = 3 pi/2 the graph reaches a 'low point', which also requires zero slope.
The figure below shows how A ' (2) represents the slope of the A(t) graph at the t = 2 point.
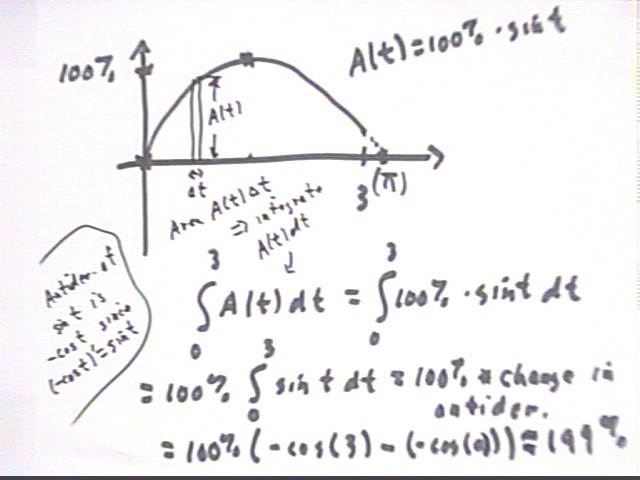
The integral of A(t) is represented by the area under the graph of A(t).
A typical small trapezoid or rectangle approximating the area over a short increment `dt is seen to have altitude A(t), representing the approximate average attention %, and width `dt, representing the time interval. So the area A(t) `dt represents the product of attention span and time interval, in units of % * month, or % -months.
A set of lower and upper Riemann sums will therefore 'squeeze' the actual area, or integral, between them, as `dt -> 0. The area is therefore represented by the integral of A(t), as indicated in the figure below.
The integral of A(t) is calculated as the change in the 'change-in-amount' function, which we understand to be the antiderivative. So we calculate the change in an antiderivative of A(t) = 100% * sin(t).
Knowing that the derivative of cos(t) is - sin(t) we conclude that - cos(t) is an antiderivative of sin(t) and use 100% * (-cos(t)) as our antiderivative to the A(t) function. We get
integral of A(t) = change in antiderivative = final value of antiderivative - initial value of antiderivative = 100% ( - cos(3) ) - 100% ( -cos(0) ) = 99% + 100% = 199%.
According to our interpretation this represents 199 %-months.
We have accumulated 199 %-months in 3 months, which is an average of about 67 %-months per month. This can be interpreted as an average attention which is 67% of maximum.
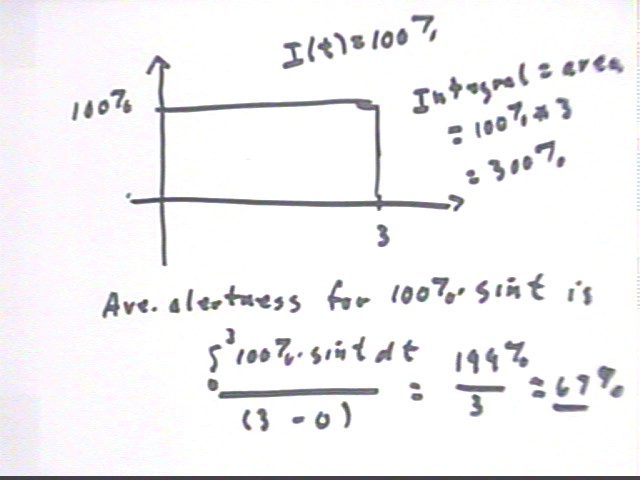
The integral of I(t) = 100% over the 3-month span is easily calculated as the area of the rectangle pictured below. We get 100% * 3 months = 300 %-months in 3 months, which of course implies an average of 100% of maximum attention.
The units of the integral would actually be %-months, not just the % indicated in the figure.
The Chain Rule.
The Chain Rule applies to composite functions.
Recall that composite functions are functions that require you to apply one function to the variable, then another function to the result.
The figure below uses the example of y = sin(t^2), in which t is first squared, then the sine of the result is calculated. This is a 'chain' of calculations, as opposed to a product of two functions. If we have a product of two functions we apply the first function to the variable, then apply the second function to the variable (not to the result of the first calculation) before we multiply the two. In a chain we apply the second function to the result of the first calculation.
The function y = sin(t^2) can therefore be represented by the composite f(g(t)), where g(t) = t^2 and f(z) = sin(z). Note that z is a 'dummy' variable (if necessary refer back to notes related to Chapter 1).

For g(t) = t^2 and f(z) = sin(z) we see that f(g(t)) = sin(g(t)) = sin(t^2).
The Chain Rule tells us that the derivative of a composite function f(g(t)) is
[ f(g(t)) ] ' = g ' (t) * f ' (g(t)).
As indicated in the figure below g ' (t) represents the rate of change due to the g function at t, and f ' (g(t)) represents the rate of change due to the f function at z = g(t). As we will see in more detail later, the chaining nature of our calculation requires that we use product of these rates.
For f(z) = sin(z) and g(t) = t^2 we get f ' (z) = cos (z) and g ' (t) = 2 t.
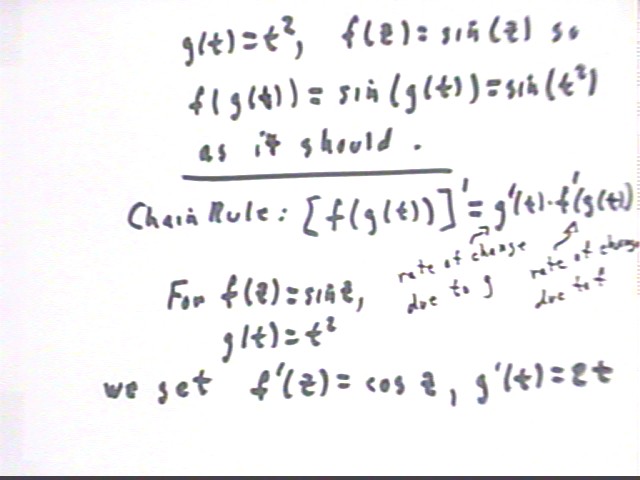
Using f ' (z) = cos (z) and g ' (t) = 2 t we apply the Chain Rule to get
[ f(g(t)) ] ' = g ' (t) * f ' ( g(t) ) =
(t^2)' * cos(g(t)) =
2 t * cos(t^2).
It is very important to note that the 'inner function' g(t) is not changed by this process. The t^2 we started with as the argument of the sine function remains as the argument of the derivative, the cosine function. This result is multiplied by the derivative 2 t of the t^2 function, but the 2 t does not appear as the argument of the 'outer function' or its derivative.
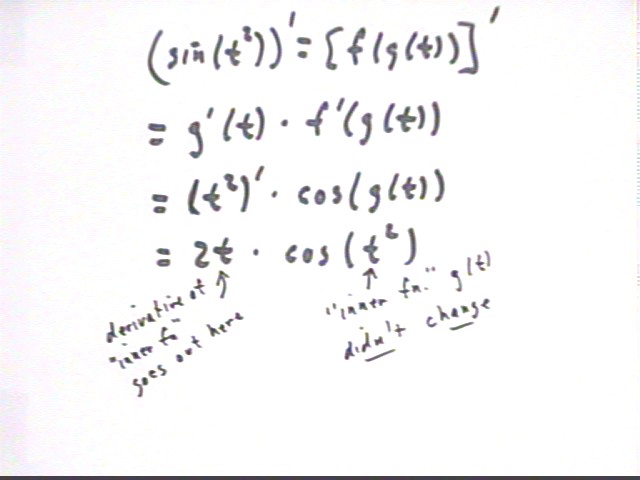
We apply the Chain Rule to the derivative of y = e^(t^2).
As indicated this function is a composite f(g(t)) of g(t) = t^2 and f(z) = e^z.
We obtain
y ' = [ f(g(t)) ] ' = g'(t) * f ' (g(t)) =
(t^2) ' * e^(g(t)) =
2t * e^(t^2).