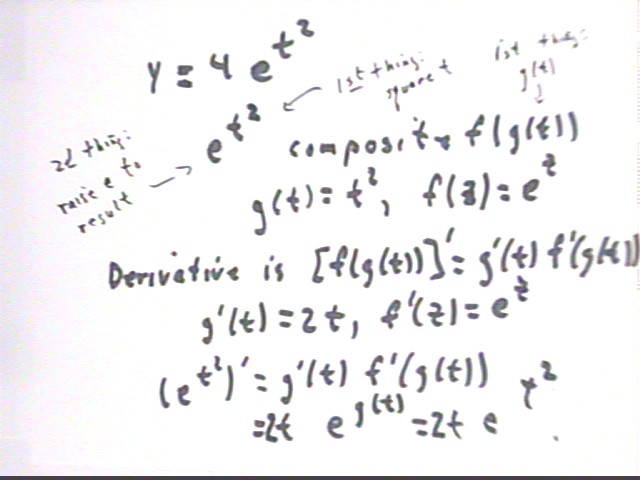
Calculus I Quiz 1108
Find the derivatives of the following:
y = 4 ( e^(t^2) )
First we will find the derivative of the function e^(t^2)
The function e^(t^2) is a composite function--given t we would first find t^2 then raise e to the resulting power. Since we 'feed' the result of one function (the squaring function) into another function (the exponential function) this 'chain' of calculations indicates that we have a composite function of the form f(g(t)).
In the form f(g(t)) we see that the first thing that 'happens' to t is the function g(t). Since the first thing that 'happens' to t in the composite function e^(t^2) is the t^2, we conclude that g(t) = t^2.
The result of the first operation is then 'fed into' the second. In the form f(g(t)) this means that g(t) is 'fed into' the f function. Since in evaluating e^(t^2) we 'feed' the t^2 into the exponential function we conclude that f must be the exponential function. Using the 'dummy variable' z we say that f(z) = e^z.
The derivatives of g(t) and f(z) are respectively (t^2) ' = 2 t and (e^z) ' = e^z.
As shown below we use the Chain Rule formula [ f(g(t)) ] ' = g ' (t) * f ' (g(t)) to obtain the derivative of e^(t^2), obtaining
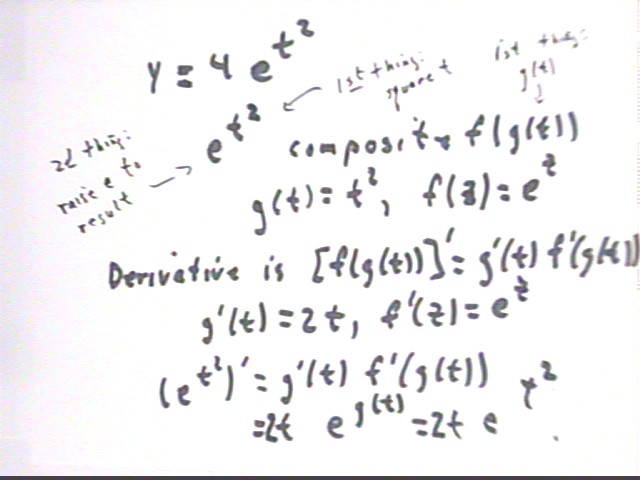
The derivative of 4 e^(t^2) is easily found using the constant rule, as shown in the first two lines below.

y = 7 e^(cos(t))
The last 5 lines of the above figure show the calculation of the derivative of y = 7 e^(cos(t)). Note that the scheme used is identical to the scheme used in all examples to date where we have taken the derivatives of composites.
y = 2 sin(.02 x^2 + 3 x - 7)
If we ask what is the first thing that 'happens' to x in the above expression the most straighforward answer is 'we square it' or perhaps 'we square it and multiply by .02'. However the next thing that happens is not that the result is 'fed into' another function, but rather that we compute 3 x, the total .02 x^2 + 3 x - 7 before we ever 'feed' our result into another function.
Our conclusion is therefore that the first thing that 'happens' to x is that it is fed into the simple function .02 x^2 + 3 x - 7. We call this a 'simple' function because in evaluation .02 x^3 + 3 x - 7 no result ever gets 'fed into' another function in such a way that the Chain Rule is required.
We see sin(.02 x^3 + 3 x - 7) as the composite f(g(x)), where g(x) = .02 x^3 + 3 x - 7 and f(z) = sin(z).
Having seen this we easily calculate g ' (x) and f ' (z) and use the results to obtain an expression for g ' (x) * f ' (g(x)), as shown below.
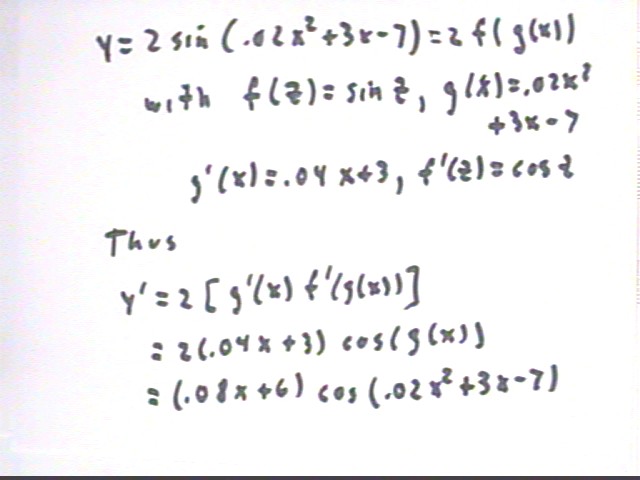
y = sin(x^2) * cos(x).
This function is first of all the product of sin(x^2) and cos(x). The product rule immediately gives us the result in the second line of the figure below.
Simplifying the second line requires that we find the derivatives of sin(x^2) and cos(x). The second is easy--(cos(x)) ' = -sin(x). However the first function, sin(x^2), is a composite.
Isolating the problem of finding the derivative of sin(x^2) we apply the Chain Rule to get the result (sin(x^2)) ' = 2 x cos(x^2).
In the next-to-last line we return to the calculation of y ', substituting the derivatives of sin(x^2) and cos(x) into the expression obtained in the second line.
The last line shows the final version of our result. These terms have no common factor and there is no simple way to combine the functions.
The velocity of a large ship leaving port is approximately given for the first hour by v(t) = 10 mph * t ( 3 - t), where t is the time in hours since leaving port. The power required to move the ship at velocity v is P(v) = 10,000 watts/(mph^3) * v^3.
At the instant when t = .5, what is the velocity of the ship and how much power does it require?
Substituting t = .5 into the expression for v(t) we easily obtain v = 12.5 mph.
Knowing that v = 12.5 mph we then substitute this value and easily calculate P(v). Note that we have used 10 kW, where kW stands for thousands of watts, in place of 10,000 watts.
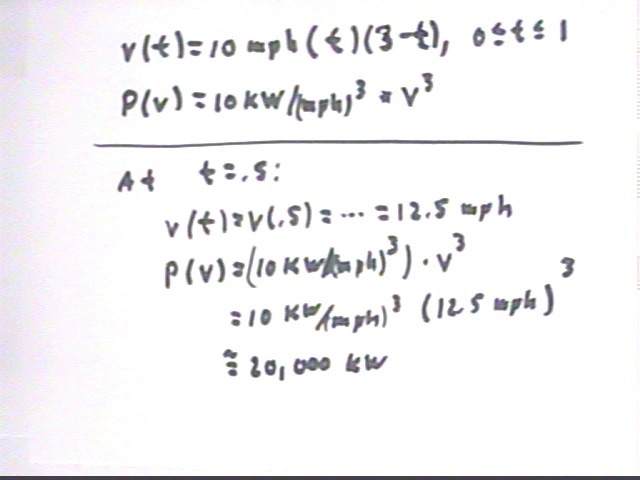
At the t = .5 instant:
Since v(t) = 10 mph * t * ( 3 - t) = 10 mph * (3 t - t^2) we see that dv/dt = 10 mph ( 3 - 2 t). Since v(t) is in mph and t in hours we conclude that dv/dt represents the rate of change of velocity with respect to t in units of mph / hr. This quantity is the answer to the question 'if we continue gaining velocity at this rate how many mph will we gain in an hour'?
We've been a little sloppy with units here. We aren't going to go into detail, which would be even more confusing, but note that careful use of units would have resulted in dv / dt = 10 mph / hr * ( 3 - 2 t). We will use this expression for dv / dt in the next paragraph.
It isn't shown in the figure below but at the t = .5 instant we get dv / dt = 10 mph / hr ( 3 - 2 t) = 10 mph / hr * ( 3 - 2 * .5) = 20 mph / hr. At the rate speed is increasing at t = .5 the speed would increase by 20 mph during the next hour. Of course we don't expect to maintain this rate of speed increase.
Note also that the abbreviation 'wrt' used below stands for 'with respect to'.
Since P is equal to 10,000 W / (mph)^2 * v^3 the rate of change of P wrt. v is 10,000 W / (mph)^3 * 3 v^2. Since P is power in watts and v is velocity in mph, dP / dv will be in units of watts / (mph). This is the answer to the question 'if power keeps increasing with speed at this rate, how much additional power will we need to speed up by 1 mph?.
In general if we multiply the rate at which power changes with respect to velocity by the rate at which velocity changes with respect to clock time we will get
dP / dt = dP / dv * dv / dt = [ 10,000 W / (mph)^3 * 3 v^2 ] * [ 10 mph/ hr * (3 - 2 t) ],
and since v = 10 mph * t * (3 - t) = 10 mph * ( 3 t - t^2) we have
dP / dt = dP / dv * dv / dt = [ 10,000 W / (mph)^3 * 3 (10 mph * (3t - t^2) )^2 ] * [ 10 mph/ hr * (3 - 2 t) ].
Note for future reference that this simplifies to 30,000,000 W / hr * ( 3t - t^2)^2 * ( 3 - 2 t) .
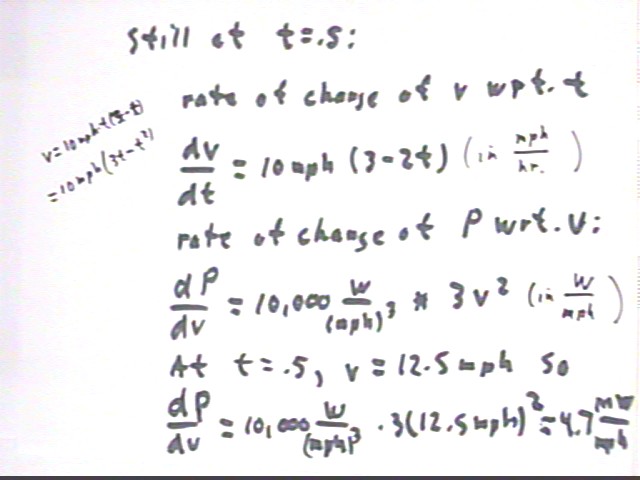
Power is changing at the rate of 4.7 MW / mph and speed is increasing at 20 mph / hr. At these rates every mph of increase in speed will require an additional 4.7 MW and every hour speed will increase by 20 mph, so in an hour power would increase by 20 * 4.7 MW = 94 MW. That is, the present rates imply that the additional power per hour is 4.7 MW / mph * 20 mph / hr = 94 MW / hr.
What we have done to find dP/dt is multiply dP/dv by dv/dt.
Write down the function P(v(t)) and find its derivative with respect to clock time.
As seen below if we substitute v(t) = 10 mph * t ( e - t) ^ 2 we get P(v(t)) = 10,000,000 W * ( 3 t - t^2) ^ 3.
We calculate dP / dt as the derivative of the composite function with 'inner' function g(t) = (3 t - t^2) and 'outer' function f(z) = z^3. We obtain the result shown below:
dP/dt = 10 MW * 3 ( 3 - 2 t) ( 3 t - t^2) ^ 2 = 30,000,000 W ( 3 - 2 t) ( 3 t - t^2) ^ 2 .
Making the same type of units correction as before we write this as
dP/dt = 10 MW * 3 ( 3 - 2 t) ( 3 t - t^2) ^ 2 = 30,000,000 W/ hr ( 3 - 2 t) ( 3 t - t^2) ^ 2.
This agrees with the expression we obtained previously by multiplying dP / dv * dv / dt.

The agreement between the two expressions is due to the fact that the g(t) function in the preceding composite was just our v(t) function, while the P(v) function was just f(z) for z = v.
The connection is shown below.
Recall the interpretations of dP/dv and dv/dt as rate of power change in watts / mph and rate of velocity change in mph / hr so that dP/dv * dv/dt = f ' (g(t) ) * g ' (t) is interpreted as rate of power change with respect to clock time in watts / mph * mph / hr = watts / hr.
