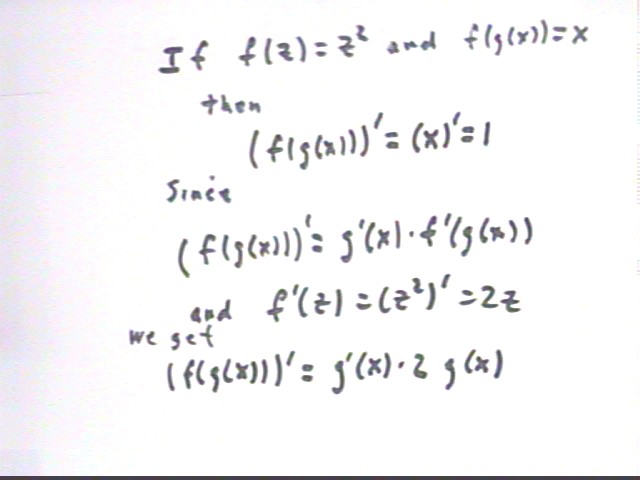
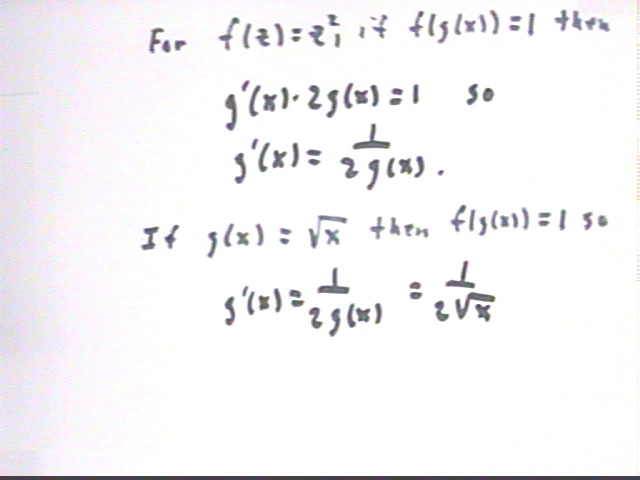
Calculus I Quiz 1111
Let g(x) be an unspecified function. Then what is simplest expression that follows from the Chain Rule for the derivative of f(g(x)), where f(z) = z^2?
[ f(g(x)) ] ' = g'(x) * f ' (g(x)).
We know nuthin' about g(x) so g(x) gonna stay g(x) and g ' (x) gonna stay g ' (x).
We know somethin' about f. We know that f(z) = z^2. So f ' (z) = 2 z.
Now we can go on with what we started in the first line.
[ f(g(x)) ] ' = g'(x) * f ' (g(x)) = g ' (x ) * 2 g(x).
If [ f(g(x)) ] ' = g'(x) * f ' (g(x)) = g ' (x ) * 2 g(x) = 1 then
g ' (x ) * 2 g(x) = 1 so that
g ' (x) = 1 / ( 2 g(x) ).
If g(x) = sqrt(x) then f(g(x)) = ( g(x) )^2 = (sqrt(x))^2 = x, so (f(g(x))) ' = (x)' = 1.
In the first 'bullet' we assumed that (f(g(x))) ' = 1 and found that for the given f(z) = z^2 we have g ' (x) = 1 / ( 2 g(x) ).
In the second 'bullet' we showed that if g (x) = sqrt(x), (f(g(x))) ' = 1. So
if g(x) = sqrt(x) then
g ' (x) = 1 / ( 2 g(x) ) = 1 / ( 2 sqrt(x) ).
These calculations are summarized in the figures below:
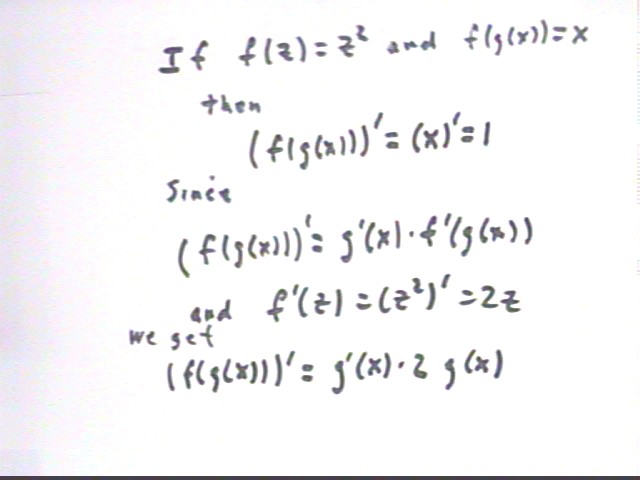
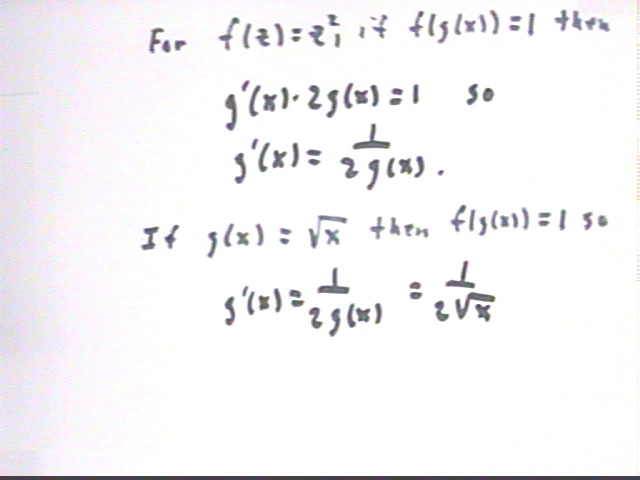
Let g(x) be an unspecified function. Then what is simplest expression that follows from the Chain Rule for the derivative of f(g(x)), where f(z) = e^z?
If [ f(g(x)) ] ' = g'(x) * f ' (g(x)) = g ' (x ) * e^g(x) = 1 then
g ' (x ) * e^g(x) = 1 so that
g ' (x) = 1 / e^g(x).
If g(x) = ln(x) then f(g(x)) = e^g(x) = e^(ln x) = x, so (f(g(x))) ' = (x)' = 1.
In the first 'bullet' we assumed that (f(g(x))) ' = 1 and found that for the given f(z) = e^z we have g ' (x) = 1 / ( e^ g(x) ).
In the second 'bullet' we showed that if g (x) = ln(x), (f(g(x))) ' = 1. So
if g(x) = ln(x) then
g ' (x) = 1 / ( e^g(x) ) = 1 / ( e^(ln x) ) = 1 / x.
These calculations are summarized in the figure below. In these figures we emphasize that the formula g ' (x) = 1 / e^(g(x)) comes directly from the definition f(z) = e^z of the function f and from the assumption that the derivative of f(g(x)) is 1, and does not in any way depend on knowing the exact form of the function g.

The fact that the derivative of f(g(x)) is 1 does, however, depend on f(g(x)) = x, which implies that g must be the inverse of f. Since we can write the inverse of the exponential function as g(x) = ln(x) we obtain the formula for the derivative of this inverse function.

Let g(x) be an unspecified function. Then what is simplest expression that follows from the Chain Rule for the derivative of f(g(x)), where f(z) = sin(z)?
[ f(g(x)) ] ' = g'(x) * f ' (g(x)).
We know that f(z) = sin(z). So f ' (z) = cos(z).
Now we can go on with what we started in the first line.
[ f(g(x)) ] ' = g'(x) * f ' (g(x)) = g ' (x ) * cos(g(x)).
If [ f(g(x)) ] ' = g'(x) * f ' (g(x)) = g ' (x ) * cos(g(x)) = 1 then
g ' (x ) * cos(g(x)) = 1 so that
g ' (x) = 1 / cos(g(x)).
This reasoning is summarized below:
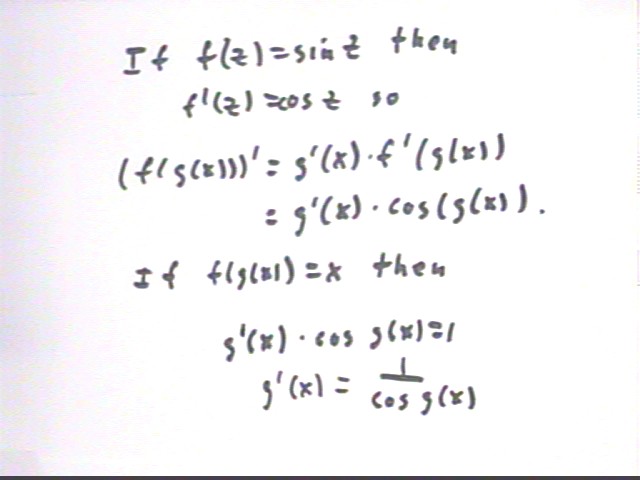
If g(x) = sin^-1(x) then f(g(x)) = sin(g(x)) = sin((sin^-1(x)) = x, so (f(g(x))) ' = (x)' = 1.
Note that sin^-1(x) is a somewhat ambiguous notation, since it could stand for 1 / sin(x). However we never write 1 / sin(x) as sin^-1(x); we would instead use the form (sin(x)) ^-1 to avoid confusion with the inverse function.
We could also avoid confusion by using the notation arcsin(x) rather than sin^-1(x).
In the first 'bullet' we assumed that (f(g(x))) ' = 1 and found that for the given f(z) = sin(z) we have g ' (x) = 1 / ( cos(g(x)) ).
In the second 'bullet' we showed that if g (x) = sin^-1(x), (f(g(x))) ' = 1. So
if g(x) = sin^-1(x) then
g ' (x) = 1 / ( cos(g(x)) ) = 1 / ( cos(sin^-1(x))) = (what in the world is this?).
To understand the expression cos(sin^-1(x)) we sketch the right triangle shown below. The side of this triangle opposite the angle sin^-1(x) is x and the hypotenuse is 1. This ensures that the sine of sin^-1(x) is x.
Using the Pythagorean Theorem we easily find the cosine of this angle to be cos(sin^-1(x)) = adjacent side / hypotenuse = 1 / sqrt(1-x^2) = 1 / sqrt(1 - x^2).
We can therefore complete our formula for g ' (x) :
g ' (x) = 1 / ( cos(g(x)) ) = 1 / ( cos(sin^-1(x))) = 1 / sqrt(1 - x^2).
Since g(x) = sin^-1(x) we have the fomula
( sin^-1(x) ) ' = 1 / sqrt(1-x^2) or
(arcsin(x) ) ' = 1 / sqrt(1-x^2).

Implicit Differentiation
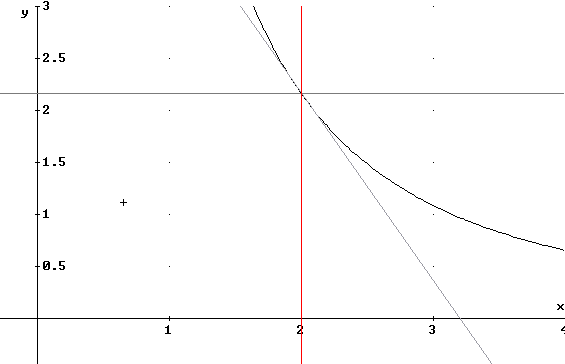
Given an equation like x^2 y + x y - 4 = 9 we understand that the set of points (x, y) satisfying this equation form a curve. Part of the curve for this function is shown in the figure below:
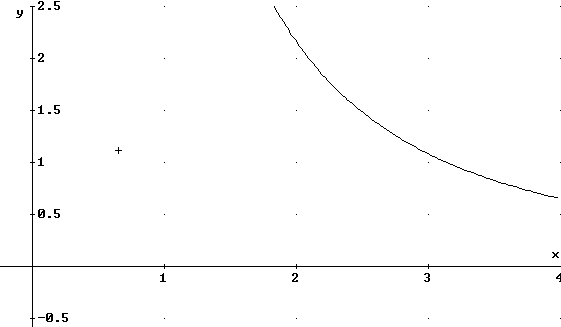
Thus y is seen to be a function of x.
We can in fact solve the given equation for y in terms of x, obtaining y = 13 / [ x(x+1) ]. This is a rational function with vertical asymptotes at x = -1 and at x = 0, etc..
The function y = 13 / [ x(x+1) ] is an explicit function of x. We could calculate the formula for its derivative.
If we change the original equation just slightly to x^2 y + x y^2 - 4 = 9 it becomes much more difficult to solve for. Though for this equation it would be possible to do so the formula we get would be pretty complicated and calculation of the derivative would be pretty tedious.
If the equation is complicated just a little bit more it becomes impossible to solve for y.
It is, however, still often possible to obtain a formula for the derivative y ' (x) in terms of x and y, allowing us to determine the slope of the graph at any point whose x and y coordinates we know.
We illustrate the process first in terms of the given equation x^2 y + x y - 4 = 9.
It isn't difficult to determine that when x = 2, we have y = 13/6. So we pose the question of finding, without use of the explicit equation, the value of y ' at the point (2, 13/6).
We note also that having found this derivative we will know the slope of the curve at the given point and we will therefore be able easily to construct line tangent to the graph at (2, 13/6).
We begin by taking the derivative with respect to x of every term of the given equation. We note that the terms x^2 y and x y are product functions so we need to apply the product rule, obtaining derivatives (x^2)' y + x^2 * y ' and x ' y + x y '. The constant terms -4 and 9 both have derivative zero.
We can take the derivative of x^2, obtaining 2 x, and of x, obtaining 1. However we cannot simplify y ' since we know that y is a function of x but we do not assume that we know the explicit form of this function.
We therefore obtain the equation 2 x y + x^2 y ' + y + x y ' = 0, which we will be able to solve for y '.

We rearrange the equation to get all terms containing y ' on one side. We then factor out y ' to get the second line shown below.
Dividing both sides of this equation by the factor x^2 + x of y ' we obtain our solution
y ' = ( - 2 x y - y) / (x^2 + x).
Substituting x = 2 and y = 13/6 we obtain y ' = -65 / 36.
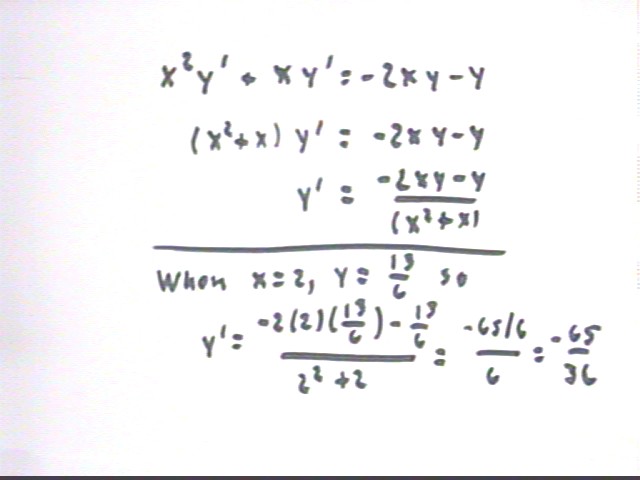
We construct the tangent line to the curve at this point, obtaining y - 16/3 = -65/36 * (x - 2).
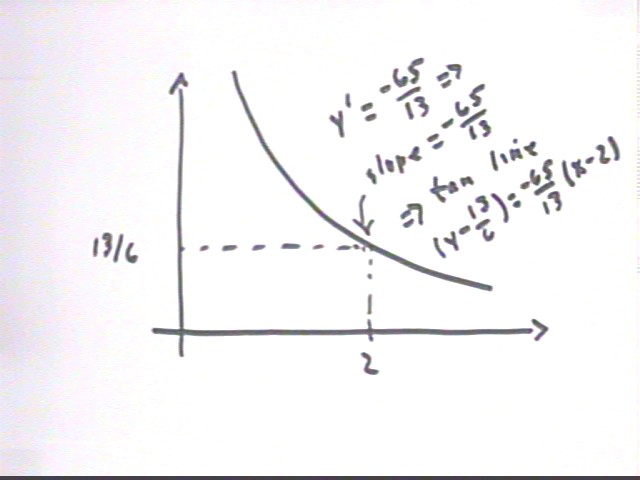
The curve and this line are plotted accurately in the figure below. We observe that the point of tangency is indeed (2, 13/6) and that the tangent line does 'fit' the curve properly.