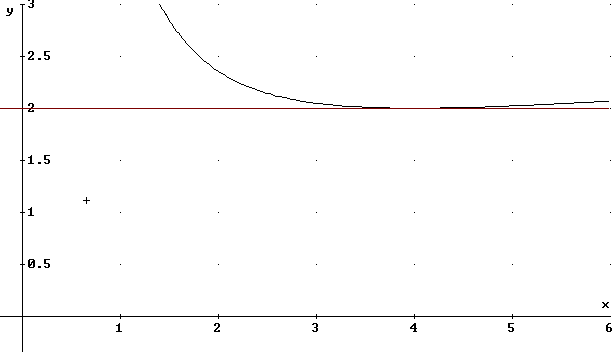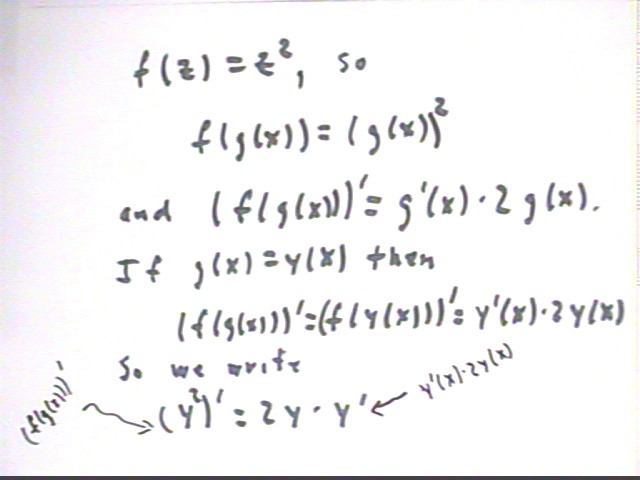
Calculus I Quiz 1113
If g(x) = y(x) and f(z) = z^2 then what is the function f(g(x))? What is the derivative of this function with respect to x?
Since f(z) = z^2 we have f(g(x)) = (g(x))^2 = (y(x))^2.
f ' (z) = 2 z.
Thus (f(g(x))) = g ' (x) * f ' (g(x)) = g ' (x) * 2 g(x) = y ' (x) * 2 y(x).
The point here is that if we are taking the derivative with respect to x of the expression y^2, that expression is a composite of the f(z) = z^2 function and the derivative is y ' * 2 y, usually written in the order 2 y y '.
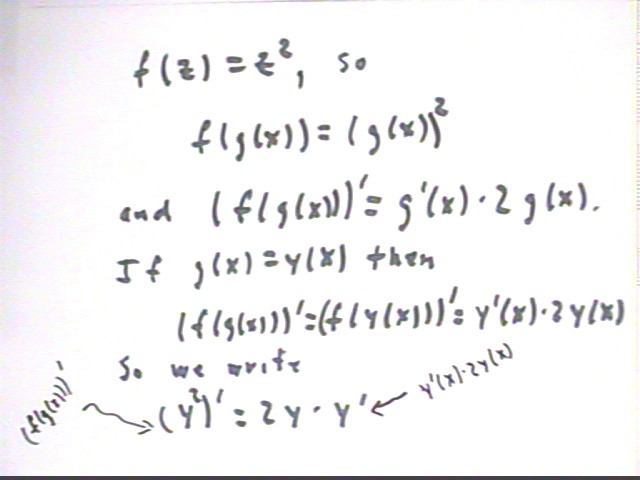
Explain why the derivative with respect to x of x^2 y^3 is given by 2 x y^3 + 3 x^3 y^2 * y ' and not by 2 x y^3 + 3 x^3 y^2.
(x^2 y^3) ' = (x^2) ' y^3 + x^2 ( y^3 ) '.
y^3 is the composite of f(z) = z^3 and g(x) = y(x) so
(y^3) ' = y ' (x) * 3 y^2(x),
which we abbreviate as y ' * 3 y ^2 or 3 y^2 y '.
Thus (x^2 y^3) ' = 2 x y^3 + 3 x^3 y^2 * y ' .
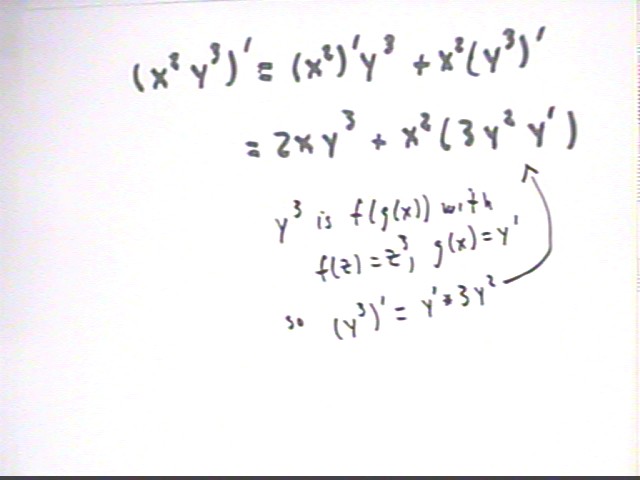
Suppose that x(t) = t^2 and y(t) = t^3 represent the x and y coordinates of an object which is moving in the x-y plane.
The next figure illustrates this situation. A table of x and y vs. t shows us that the object moves from (0, 0) at t = 0 to (1, 1) at t = 1 then to (4, 8) at t = 2. A rough curve is depicted, but note that this curve doesn't have all the correct characteristics between x = 0 and x = 1 (plot the t = 1/2 and t = .1 points to get a pretty good idea of what's wrong with the curve as sketched).
You would walk from x = 0 to x = 1 during the first second, from t = 0 to t = 1, therefore averaging 1 unit / second. From t = 1 to t = 2 you would walk from x = 1 to x = 3, therefore averaging 3 units / second. Average velocities are calculated using `dx / `dt.
The instantaneous velocities would be found by evaluating the derivative vx = dx/dt at each point. Since x = t^2 we have vx = dx/dt = 2 t. This is the velocity function for motion in the x direction.
Thus
These results are summarized in the vx vs. t table in the next figure.
Instantaneous y velocities are found using the function vy = dy/dt = (t^3) ' = 3 t^2. Thus
These results are summarized in the vy vs. t table in the figure.
As indicated on the graph, at the t = 1 point (1, 1) we have vx = 2 and vy = 3.
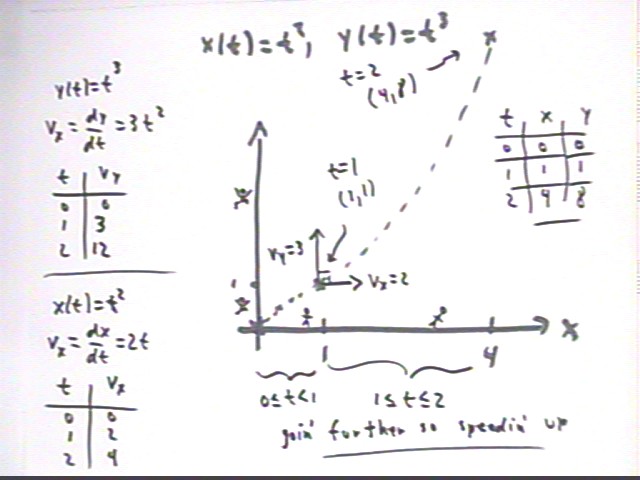
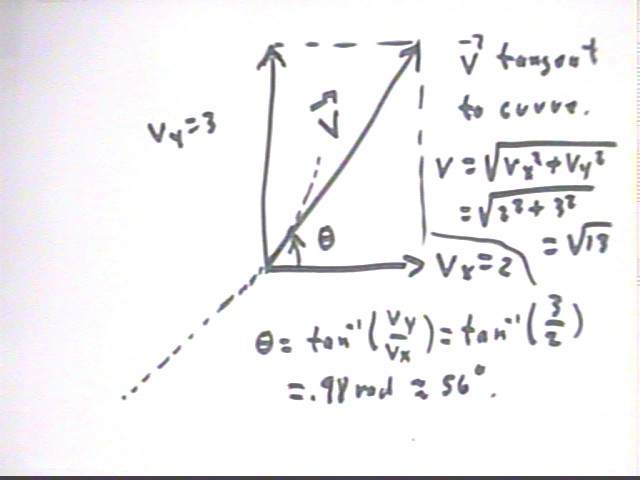
An enlarged figure showing the curve (dotted line, not particularly accurate) and the x and y velocities at the t = 1 point (1,1) is depicted below. We see that the velocity has x and y components vx = 2 and vy = 3, resulting in a velocity with magnitude
At the t = 0 point we have vx = vy = 0 so v = 0.
At the t = 2 point we have vx = 4 and vy = 12 so that
The angle at each clock time will be the angle whose tangent is vy / vx so we have
Note that at t = 0 the angle is undefined, since 0 / 0 is undefined.
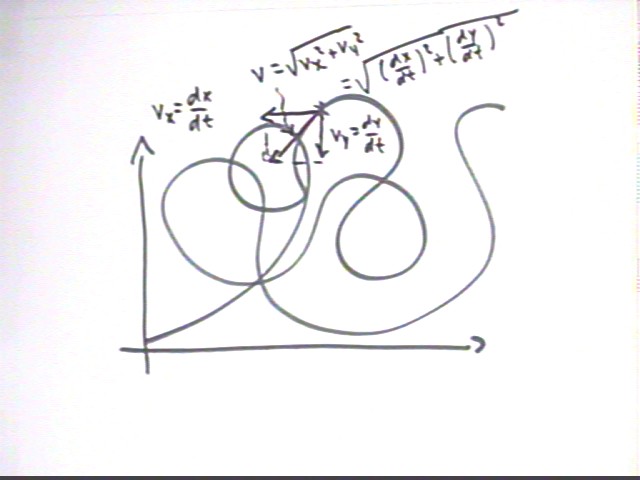
In general a set of parametric equations for x and y can form a very complex curve in the x-y plane.
For any such set of equations we can easily calculate the position at any desired value of the parameter (in this case the parameter is t). If we can find the derivatives of the parametric equations we can also then find the components vx = dx/dt and vy = dy/dt of the velocity at that point.
We calculate the magnitude of the velocity as v = sqrt(vx^2 + vy^2) = sqrt( (dx/dt)^2 + (dy/dt)^2 ) as well as the direction, which is arctan(vy / vx) whenever vx >0 and arctan(vy / vx) + 180 deg if vx < 0.
Suppose we wish to find parametric equations for a straight line running through (3, 2) to (9, 6). There are many different parametric equations for this line. We find two different sets of equations:
First we note that the slope of the line must be rise / run = 4 / 6 = 2/3. If we start at the point (3, 2) when t = 0 and let our displacement in the x direction equal t we will have displacement 2/3 t in the y direction, which places us at the point (3 + t, 2 + 2/3 t). Thus the equations
will for any value of t place us on the line.
Alternatively we could think of moving at uniform velocity from (3, 2) to (9, 6) as t goes from 0 to 1. In this case we must move 6 units in the x direction and 4 in the y direction during the interval `dt = 1. Since we start from x = 3 and y = 2, our position function will be
The condition for being on the line is that slope = (y - 2) / (x - 3) be the same slope 2/3 as the slope between the two given points.

In fact any set of equations of the form
will keep us o
n this line as long as b / a = 2/3. This is so since in that case the x displacement from (3,2) will be a t and the y displacement will be b t, so that
We could even describe the line by a set of equations
since in this case x and y displacements from (3, 2) are a t^2 and b t^2, giving us
Using the t^2 gives us varying 'speed' along the line (note that dx / dt and dy / dt are now linear functions of t, implying variable speed).
We now find the tangent line to the curve y^2 = x^3 / (x y - 4) at the point (4, 2).
Substituting x = 4 and y = 2 into this equation gives us the identity.
We don't want to deal with a denominator so we multiply both sides by the denominator x y - 4, noting that because we can't multiply by zero we must exclude from the domain of definition any point for which x y = 4.
We obtain the equation (x y - 4) y^2 = x^2, which will will imlictly differentiate.
The process is illustrated below. Note the following:

We continue to simplify, then to solve the equation in the figure below. The first line uses only the fact that (y + x y ' ) * y^2 = y^3 + x y^2 y '.
In the second line we isolate all terms with factor y ' on one side of the equation.
In the third line we factor out y ' and in the fourth line we divide by the coefficient of y ' to get our expression for y '.
We substitute x = 4 and y = 2 into the expression for y ', obtaining y ' = 0.
This tells us that the y vs. x curve has slope 0 at the point (4, 2).
The tangent line is therefore
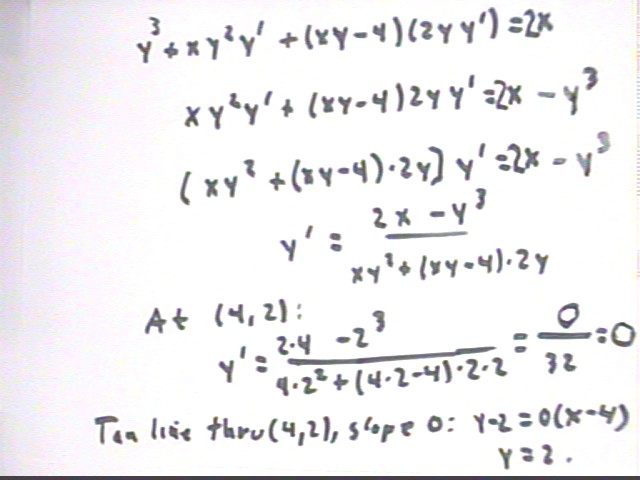
The graph below shows the y vs. x curve, obtained by entering and graphing the equation y^2 = x^2 / ( x y - 4).
The graph also shows the tangent line y = 2.
We note that the line y = 2 does indeed appear to be tangent to the curve at the point (4, 2).