Notes from Class 1115

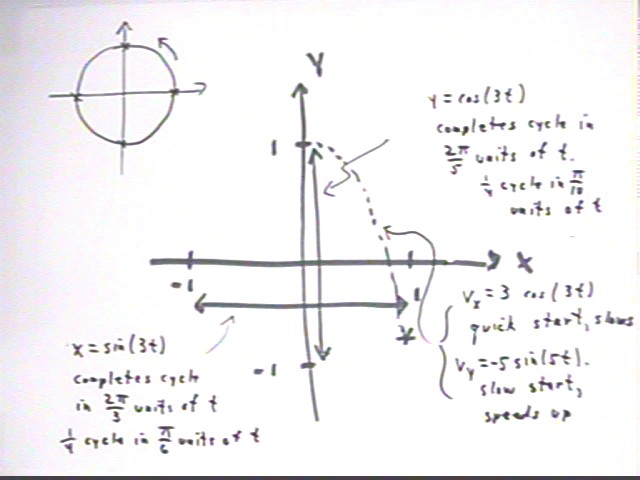
Calculus I Quiz 1115

If x = sin(3 t) and y = cos(5 t) then what does the graph of y vs. x look like for 0 <= t <= 2 pi?

Considering the reference-circle model of the sine and the cosine we see that 

• x = sin(3t) starts when t = 0 at x = 0.  x then increases to 1 before decreasing to 0 then to -1 before returning to 0 and starting the cycle over.
• For 0 <= t <= 2 pi we have 0 <= 3 t <= 6 pi, telling us that for 0 <= t <= 2 pi the x coordinate passes through 3 complete cycles, corresponding to 3 trips around the reference circle.
• Similar analysis of y = cos(5 t) tells us that the y motion starts at y = +1 and proceeds through 5 complete cycles for 0 <= t <= 2 pi.
• The times required to complete full cycles and quarter-cycles are respectively 2 pi / 3 and pi / 6 for the x coordinate and 2 pi / 5 and pi / 10 for the y coordinate. 
• As the x coordinate goes from 0 to 1 for the first time, the y coordinate, whose cycle is shorter, moves well past its x = 0 position.  The x coordinate will start out changing quickly and will slow, while the y coordinate will start out slowly and speed up as it moves toward 0, slowing gradually after passing 0.  This gives us the graph segment shown below.

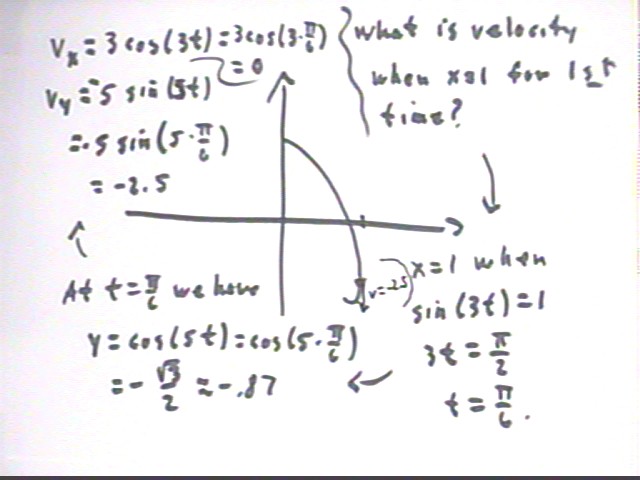
To find the position and velocity when x first reaches 1 we first set sin(3t) = 1 to determine that this occurs when t = pi/6.  

Then plugging t = pi/6 into y = cos(3t) we find that y = -sqrt(3)/2, or about -.87.

The x and y velocities will be the derivatives vx = 3 cos(3t) and vy = -5 sin(5t).  At t = pi/6 we find that vx = 0 (no surprise there) and vy = -2.5.

Thus when x = 1 for the first time we have a velocity of 2.5, directed downward in the y direction.

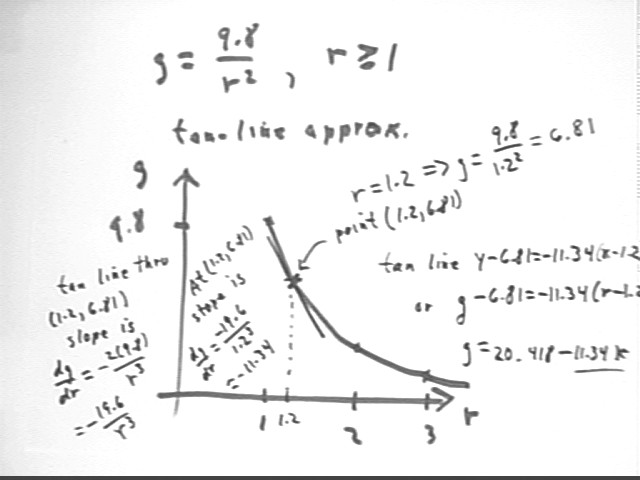
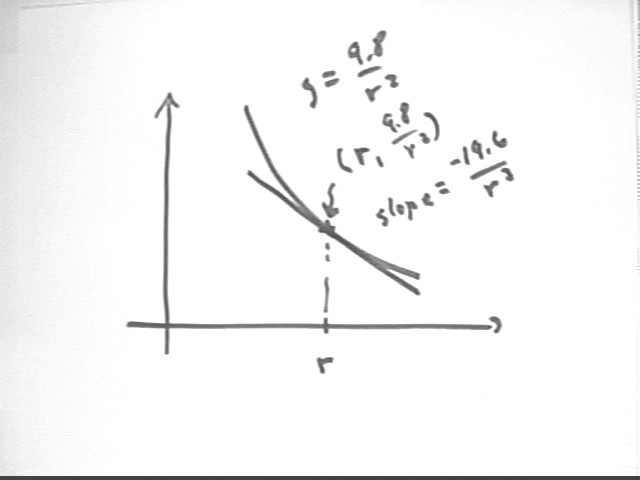
The acceleration of gravity at distance r from the center of the Earth, with r given in units of Earth radii, is

g = 9.8 / r^2, r >= 1.

• What is the tangent-line approximation to this function at r = 1.2?  According to this approximation how much does g change between r = 1.2 and r = 1.3?

• At arbitrary r what is the tangent-line approximation to the change `dg in g corresponding to a change `dr in r?  Think in terms of the tangent-line approximation to the function g at the point (r, g) = (r, 9.8/r^2).

The function  g = 9.8 / r^2 has the graph shown below.  The r = 1.2 point is (1.2, 6.81) and the slope is dg / dr = - 19.6 / r^3 evaluated at r = 1.2 to give us dg / dr = -11.34, approx..

This yields tangent line g = 20.418 - 11.34 r.

• At arbitrary r what is the tangent-line approximation to the change `dg in g corresponding to a change `dr in r?  Think in terms of the tangent-line approximation to the function g at the point (r, g) = (r, 9.8/r^2).

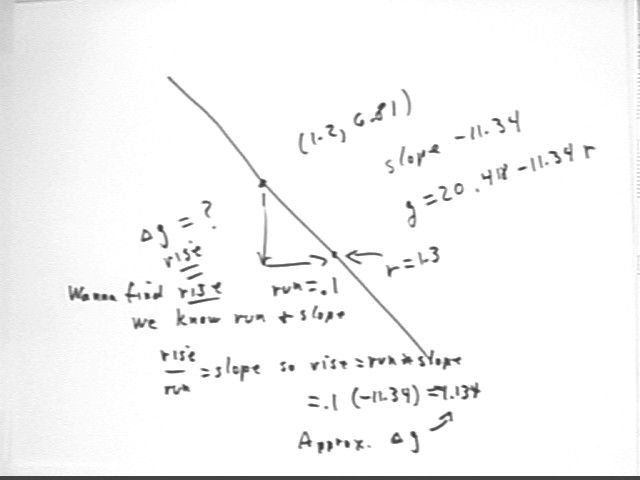
The change in g corresponds to a change of `dr = .1.  The tangent-line approximation to this change could be found by plugging r = 1.3 into the equation of the tangent line and subtracting the r = 1.2 value from the approximate r = 1.3 value that results.  However there's a simpler way.

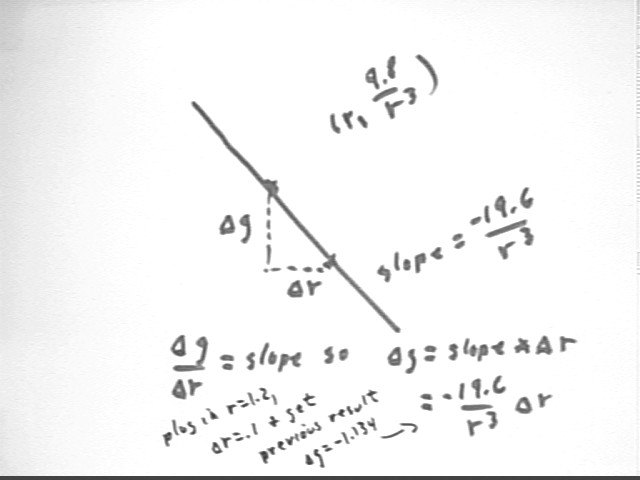
The figure below shows the geometry of the situation.  The change along the tangent line will be the change `dg, which is a 'rise', corresponding to the 'run' `dr = .1.  Since we know that the slope is -11.34, approx., it is easy to find the tangent-line approximation to `dg.

Generalizing this approach, at the unspecified coordinate r we have g = 9.8 / r^2, so our graph point is (r, 9.8 / r^2) and the slope is dg / dr = -19/6 / r^3.

To find an  approximate `dg corresponding to a given `dr we multiply `dr by the slope, obtain the approximation `dg = -19.6 / r^3 * `dr.

Approximating the change we found previously we find that for `dr = .1 and r = 1.2 the change in g is approximately `dg = -19.6 / (1.2)^3 * .1 = -1.134, the same result we obtained before.

The expression `dg = -19.6 / r^3 * `dr can be applied to any r and any `dr; however for smaller `dr we get a better approximation to `dg.

The period of a pendulum is T = .2 sqrt(L). 

• What is the tangent-line approximation to this function at L = 12?  According to this approximation how much does T change between L = 12 and L = 13?

• At arbitrary L what is the tangent-line approximation to the change `dT in T corresponding to a change `dL in L?  Think in terms of the tangent-line approximaton to the function T at the point (L, T) = (L, .2 sqrt(L) ).