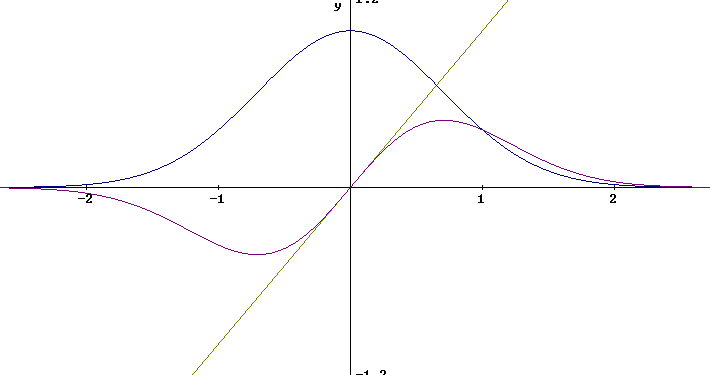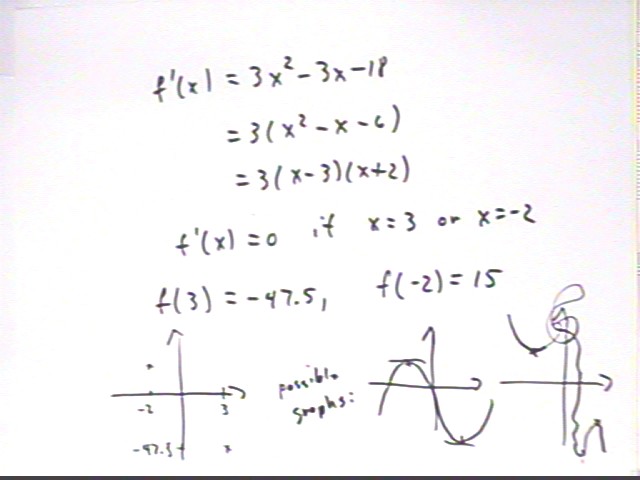
Calculus I Quiz 1120
At what points is the derivative of f(x) = x^3 - 3/2 x^2 - 18 x - 7 equal to zero?
f ' (x) = 3 x^2 - 3 x - 18. We have f ' (x) = 0 is
3 x^2 - 3x - 18 = 0. The LH side factors into 3 ( x^2 - x - 6), then into 3 (x - 3)( x + 2) and
3(x-3)(x+2) = 0 for x = 3 and x = -2.
When x = 3 we have f(x) = -47.5 and when x = -2 we have f(x) = 15.
Possible graphs are shown in the figure below. The graph must 'level off' when the derivative is 0, as depicted.
The somewhat absurd graph at lower right really isn't possible, not only because it doesn't represent a function but because if the function hits a 'local low point' at (-2,15) then to get down to (3, -47.5) it would have to turn around at some point; if the function is continuously differentiable, as is the case for a polynomial, it would have to 'level off' at the turn-around point, so the derivative would have to be zero at such a point. Since the only zeros of the f ' (x) function are at x = 3 and x = -2, this can't happen.
The second derivative f '' (x) = 6 x - 3 tells us where the graph is concave up, concave down, and where the concavity changes.
At x = -2 we see that f '' ( x) = f '' (-2) = -15, indicating downward concavity and confirming our suspicion that the graph reaches a relative maximum at (-2, 15).
Similarly we see that at x = 3 the 2d derivative is positive, indicating upward concavity and a relative minimum.
As indicated on the graph, f ''(x) = 0 when 6x - 3 = 0, i.e., at x = 1/2. For x < 1/2 the 2d derivative is negative and the graph is concave down, while for x > 1/2 the 2d derivative is positive and the graph is concave up.

Using this information as well as the solutions to f(x) = 0 (which gives us the x intercepts, and which for this particular cubic function we obtain with a calculator since no reasonable effort allows us to factor it) and the y-intercept (0, f(0) ) = (0, -7), we can construct a good graph of this function.
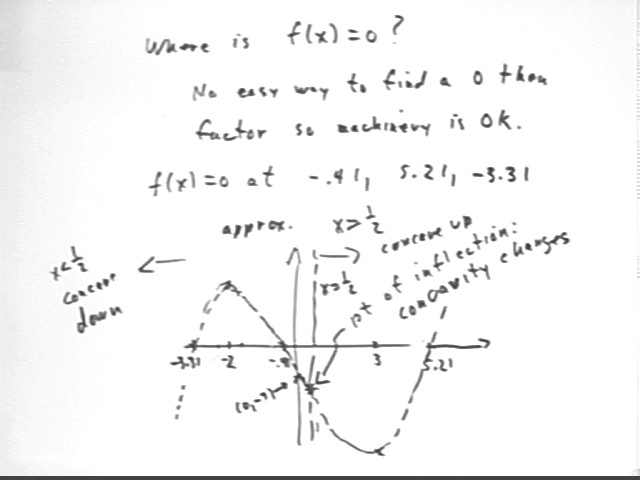
You should verify that the graph depicted below agrees with our analysis.
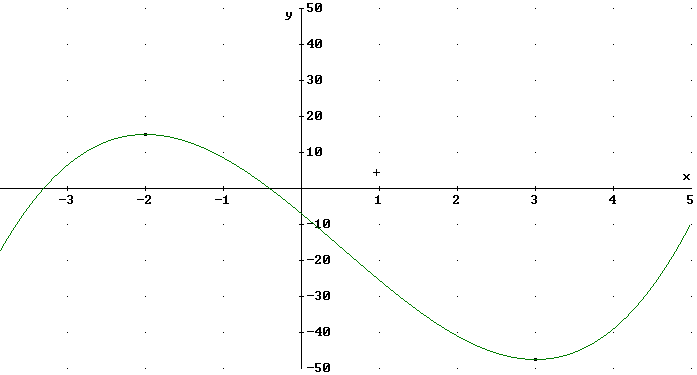
Construct a graph of f(x) = x e^-(x^2).
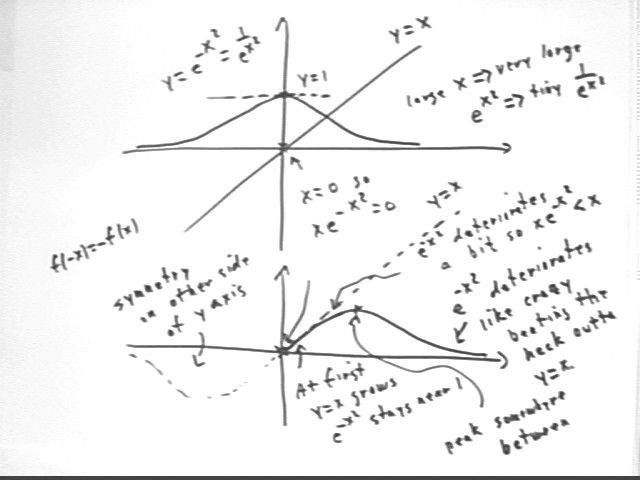
We construct the graph by starting with graphs of y = x and y = e^-(x^2), as depicted below. We note that e^-(x^2) = 1 / e^(x^2) takes its max value 1 at x = 0 and that due to the rapid increase of e^(x^2) for x > 1 the function rapidly approaches zero. For x close to zero x^2 remains very close to 0 and e^-(x^2) remains close to 1.
At x = 0 we have x e^-(x^2) = 0 so the graph starts at the origin. For small x, e^-(x^2) stays close to 1 so the graph of x e^-(x^2) stays close to the y = x graph. However e^-(x^2) does deteriorate from its original y = 1 value and as a result the graph of x e^-(x^2) deteriorates from the y = x line on which it begins.
Before long the value of x^2 becomes significant and e^-(x^2) begins to more and more rapidly approach zero, soon 'deteriorating' much faster than y = x with its constant rate of change can increase. This pulls the graph of x e^-(x^2) back to the x axis.
Somewhere between its initial increasing behavior and its large-x approach to 0 the function will reach its maximum. We'll use calculus to find this point and more about the behavior of the function.
Note that due to the nature of the symmetry of f(x), with f(-x) = - f(x), the graph to the left of the y axis is a 'negative reflection' of the graph to the right.
f ' (x) = (x) ' e^(-x^2) + x ( e^-(x^2)) ' .
e^-(x^2) is a composite of f(z) = z^z with g(x) = - x^2; derivative is -2 x e^(-x^2). So
f ' (x) = 1 e^(- x^2) + x ( -2x e^(-x^2) )
= ( 1 - 2 x^2 ) e^(-x^2).
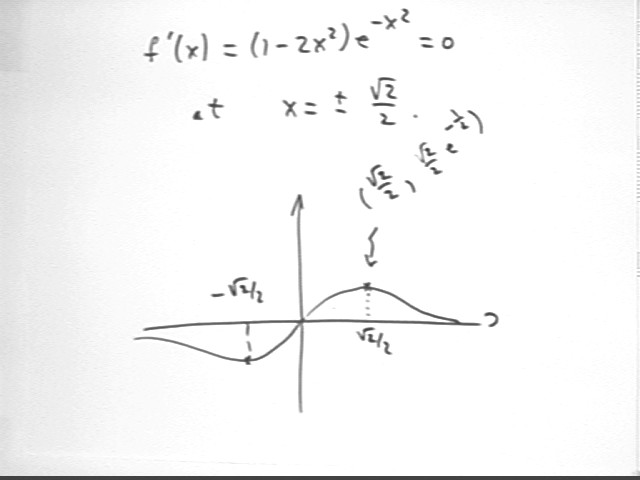
f ' (x) = 0 when (1 - 2 x^2) = 0 and when e^-(x^2) = 0. The latter cain't happen since e^(-x^2) is always positive, though really tiny for most values of x. So
f ' (x) = 0 when 1 - 2 x^2 = 0. Solving we get x = +-sqrt(2) / 2.
We conclude that the max value must be occurrin' at (sqrt(2)/2, sqrt(2)/2 * e^(-1/2) ).
f '' (x) = [ (1 - 2 x^2) e^(-x^2) ] '
= (1 - 2x^2) ' * e^(-x^2) + (1 - 2 x^2) (e^(-x^2)) '
= -4x * e^(-x^2) + ( 1 - 2 x^2) ( - 2 x e^(-x^2) )
= ( - 6 x + 4 x^3 ) e^(-x^2).
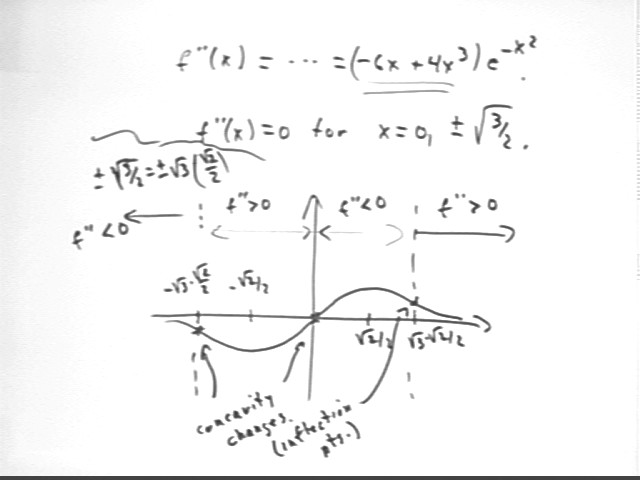
f ''(x) = 0 when -6x + 4 x^3 = 0, i.e., when
2x ( -3 + 2 x^2) = 0. This occurs if
x = 0 or -3 + 2x^2 = 0, i.e., when
x = 0 or x = sqrt(3/2) or x = -sqrt(3/2).
At x = -sqrt(2)/2 we have f '' (x) >0 and
at x = +sqrt(2)/2 we have f '' (x) <0 ,
confirming that we have a max at +sqrt(2)/2 and a min at -sqrt(2) / 2.
As depicted below the 2d derivative is negative up to x = -sqrt(3) * sqrt(2) / 2, then positive up to x = 0, then negative up to x = sqrt(3) * sqrt(2) / 2, then positive from that point on. The function will be accordingly concave down and concave up.
The graph below assembles this information:
Compare with an accurate graph: