Calculus I Quiz 1122
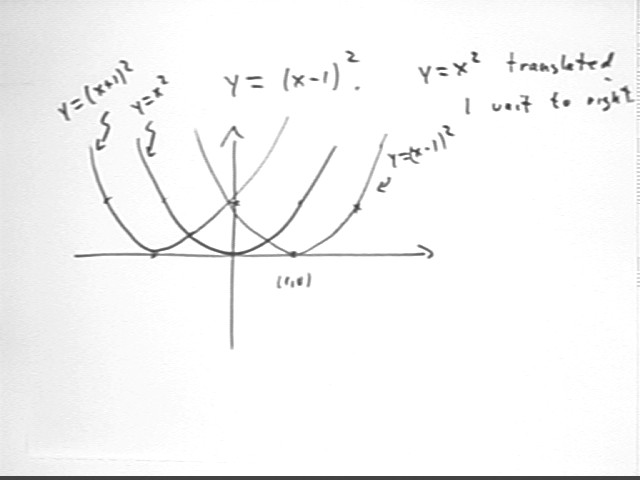
Sketch the graphs of the functions y = (x - h)^2 for h = -1, h = 1 and h = 0.
Using standard precalculus techniques we see that the h = -1 and h = 1 functions y = (x + 1)^2 and y = (x - 1)^2 have graphs which are translated respectively -1 units and 1 unit in the x direction from the y = x^2 graph, as depicted below.

The derivative of f(x) = (x - h)^2 is f ' (x) = 2 ( x - h), as depicted below.
We thus have f ' (x) = 0 when x = h.
The tangent line to the graph of f(x) = (x - h)^2 is therefore zero at x = h, which coincides with our previous graphs, which show that the vertex of the parabola will occur at x = h (i.e., at x = 1 when h = 1, at x = -1 when h = -1, etc.).

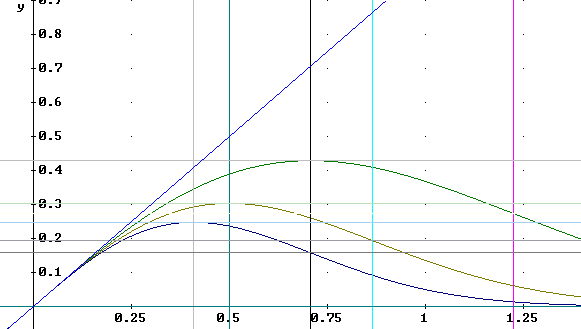
Sketch the graphs of the functions y = x e^(-k x^2) for k = 1, 2, and 3.
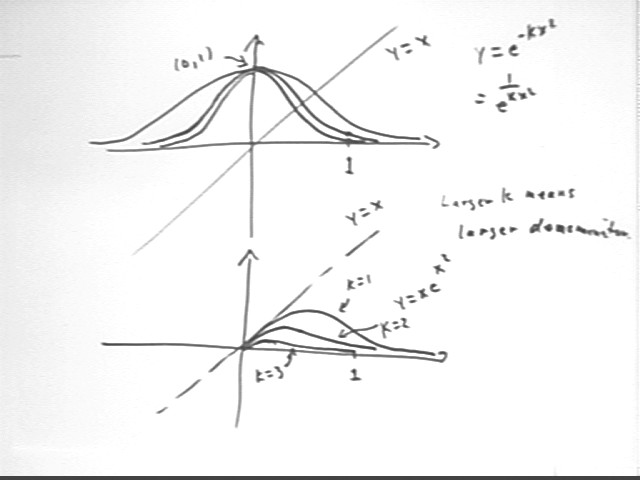
We construct the graphs by first sketching the graphs of y = x and y = e^(- k x^2).
The graphs of y = e^(- k x^2) will have the same characteristics as that of y = e^(- k x^2), which was sketched in the preceding class. At x = 0 we have y = 1; the function then 'deteriorates', slowly at first then more and more rapidly, as | x | increases.
The x = 1 points will have y values e^-k = 1 / e^k; since 1 / e^1 = .38, 1 / e^2 = .12 and 1 / e^3 = .04, all approximate we see that by the time x = 1 the graphs of y = e^(-k x^2) will have 'deteriorated' as indicated in the figure below.
As seen in the preceding class the values of y = x e^(-k x^2) stay close to the values of x as long as e^(-kx^2)) stays close to 1, then as the values of the exponential 'deteriorate' then quickly overcome the tendency of x to increase and 'bend' the graph toward the x axis. For the k = 1, 2 and 3 functions the 'deterioration' for increasing x is more and more rapid, yielding a graph much like that shown in the second graph below.
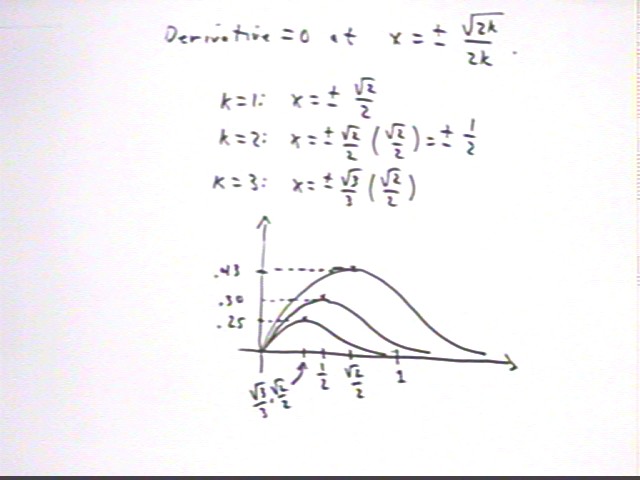
At what point(s) is the derivative of f (x) =x e^(-k x^2) zero?
The 'peak' of each function will occur when the derivative is zero. In order to determine the locations of these peaks we calculate the derivative of y = x e^-(k x^2) and set the derivative equal to zero, obtaining
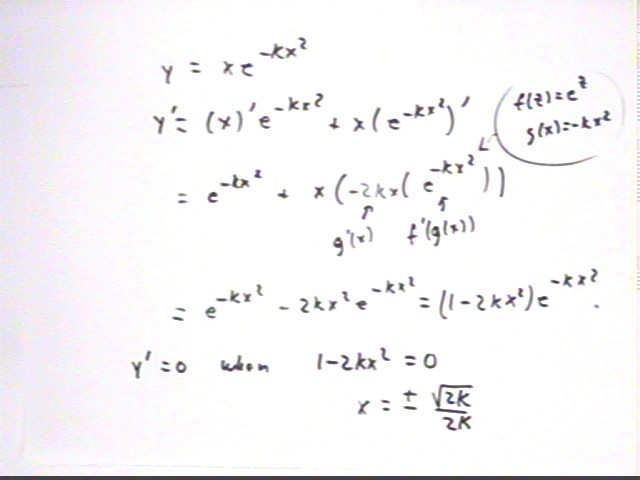
For k = 1, 2 and 3 the peak occurs at x = sqrt(2) / 2, x = sqrt(2) / 2 * sqrt(2) / 2 = 1/2 and x = sqrt(3) / 3 * sqrt(2) / 2. These points are depicted on the graph below. The y values are obtained by substituting the respective x values into the function
We note that by the nature of the symmetry of this function we will have relative minimum values at x = -sqrt(2) / 2, x = -sqrt(2) / 2 * sqrt(2) / 2 = -1/2 and x = -sqrt(3) / 3 * sqrt(2) / 2. The graph isn't depicted here for negative x values; if necessary consult notes from the preceding class to see the nature of the symmetry.
Concavity is determined by the second derivative. The second derivative is calculated below and set equal to zero. We find that concavity is zero at x = 0 and at x = +-sqrt(3) * sqrt(2k) / (2k)--about 1.7 times as far out along the x axis as the zeros of the first derivative.
It is easy to verify that the concavity indeed changes sign at each of the points where it is zero--i.e., the second derivative function changes from positive to negative or from negative to positive at each of its zeros.
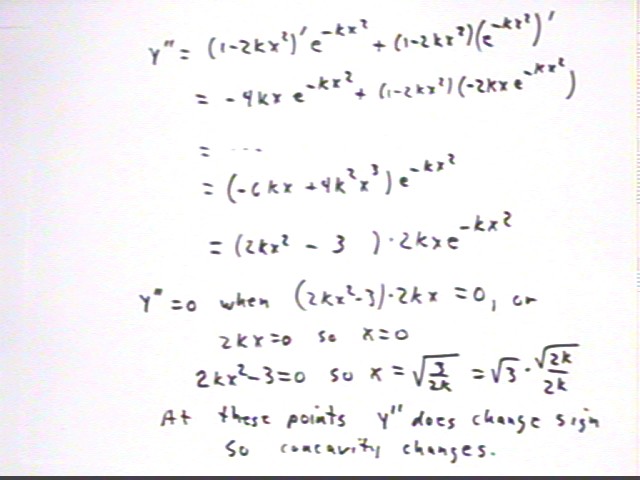
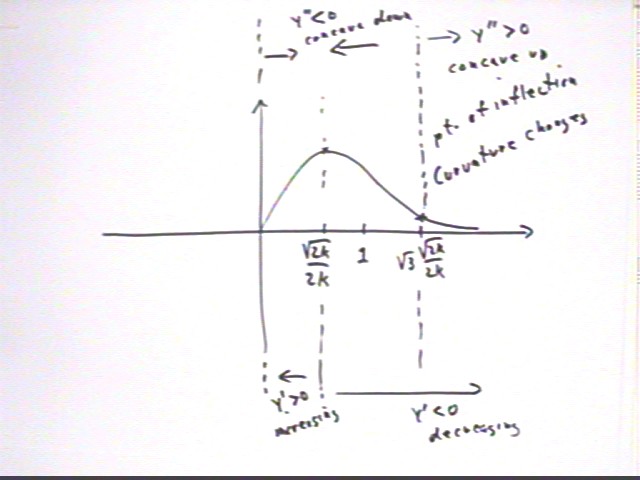
Plugging the coordinates of appropriate points into the second-derivative function we find that the second derivative is negative on the interval 0 < x < sqrt(3) * sqrt(2k) / (2k) and positive for sqrt(3) * sqrt(2k) / (2k) < x. The second derivative is seen to change from negative to positive at x = sqrt(3) * sqrt(2k) / (2k), though the sketch below doesn't show this particularly well (the graph in the sketch appears to change concavity a little 'early'). The second derivative also changes sign at x = 0 but since the graph isn't depicted for negative x this change isn't shown on the graph.
The first derivative is positive 0 <= x < sqrt(2k) / (2k) and negative for sqrt(2k) / (2k) < x, so that the function is increasing on the first interval and decreasing on the second.
The graph below depicts the y = x function with the k = 1, 2 and 3 members of the family y = x e^(-k x^2):