Calculus I Quiz 1125
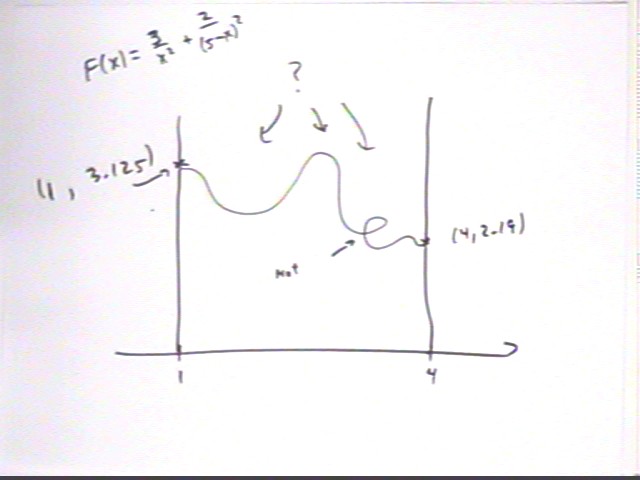
The force on a charged particle is given by F(x) = 3 /x^2 + 2/(5-x)^2. Find the maximum and minimum force on the particle on the interval 1 < x < 4.
We first sketch a graph of the function on the interval, initially specifying only the points at x = 1 and x = 4. As far as we're concerned the graph between these point could be just about anything, though since the function is single-valued the loop can't really occur.

On the interval 1 < x < 4 the value of F(x) goes from F(1) = 3 / 1^2 + 2 / (5-1)^2 = 3.125 to F(4) = 3 / 4^2 + 2 / (5-4)^2 = 2.19 approx.. The value of F(x) therefore decreases on the interval.
To see whether there are relative maxima and/or minima on the interval we see if F ' (x) = 0 at any point in the interval.
F ' (x) = -6 / x^3 + 4 / (5-x)^3,
so that F ' (x) = 0 when
-6 / x^3 + 4 / (5-x)^3 = 0. Multiplying numerator and denominator by x^3 ( 5-x)^3 we obtain
-6(5-x)^3 + 4 x^3 = 0 or
-6(5^3 + 3 * 5^2 * (-x) + 3 * 5 * (-x)^2 + (-x)^3) + 4 x^3 = 0 which gives us
-750 + 300 x - 90 x^2 + 6 x^3 + 4 x^3 = 0 or
10 x^3 - 90 x^2 + 300 x - 750 = 0, simplifying to
x^3 - 9 x^2 + 30 x - 75 = 0.
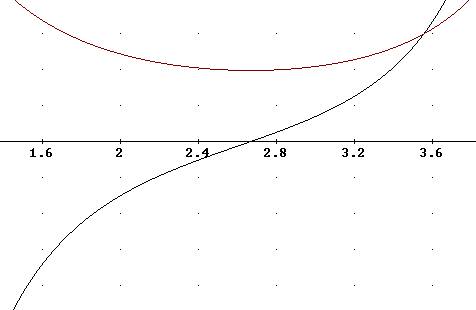
The figure below depicts these calculations.
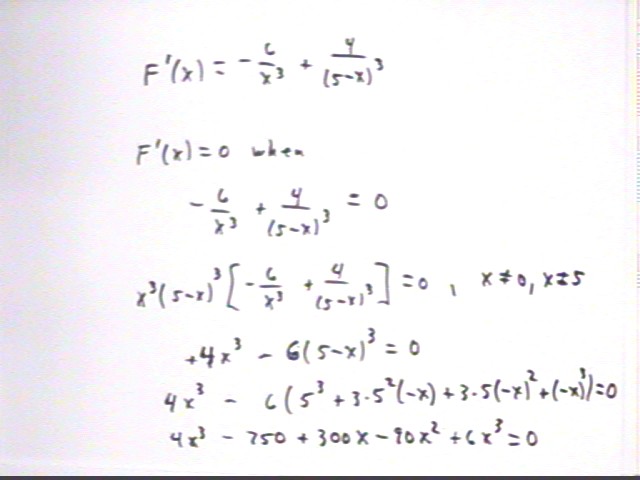
The figure below completes the calculation of the equation x^3 - 9 x^2 + 30 x - 75 = 0. It is clear that this equation has at least one zero, since it goes continuously from large negative values to large positive values, approaching -infinity and +infinity for large negative and positive x. It is unclear what happens between these extremes--the function could have as many as two relative extrema and three zeros.
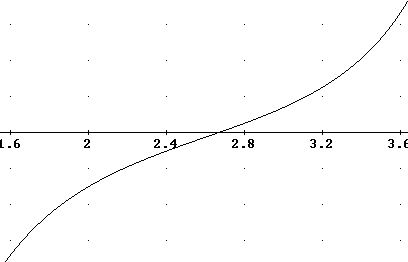
Resorting to machinery we first see just complex zeros; however we know that there must be at least one real zero and we look more closely and see that there is a real zero at = 2.669, approx., and no other real zeros.
We conclude that a graph of F ' (x) must pass through its only zero as it goes from negative to positive.
There is only one real solution of this equation, which is x = 2.669, approx.
A graph of F ' (x) vs. x shows that for 1 < x < 4, F '(x) is a continuous and strictly increasing function, which therefore changes from negative to positive at x = 2.669, approx., so that the slope of the F(x) graph goes from negative to positive at this point. This indicates that x = 2.669 is a minimum for the function.

A more accurate graph of F ' (x) is shown below. The vertical spacing between the 'dots' is .4 units.
At x = 2.669 we get F(x) = F(2.669) = .789, approx. The graph therefore has the characteristics indicated in the figure below, with F ' (x) increasing over the entire interval 1 < x < 4 so that the graph is concave up. F ' (x) will be negative for x < 2.669 and positive for x > 2.669.
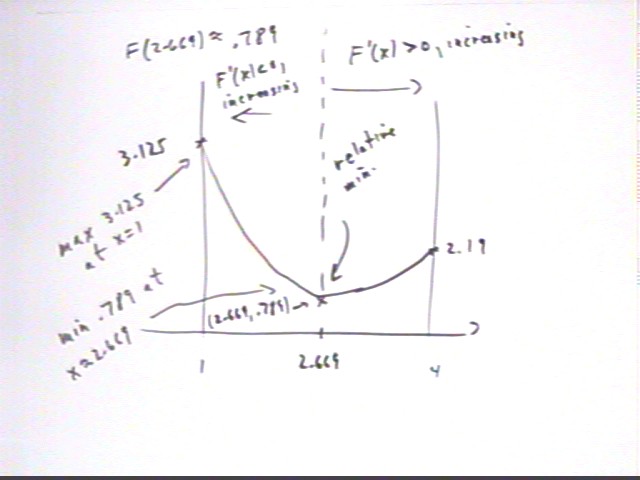
The graph below is an accurate representation of F(x) and F ' (x). We note that the greater the magnitude of F ' (x) the steeper the graph of F(x), the monotone increasing nature of F ' (x) and the resultant upward concavity of F(x), and the zero of F ' (x) at x = 2.669 corresponding to the minimum of F (x) at x = 2.669.
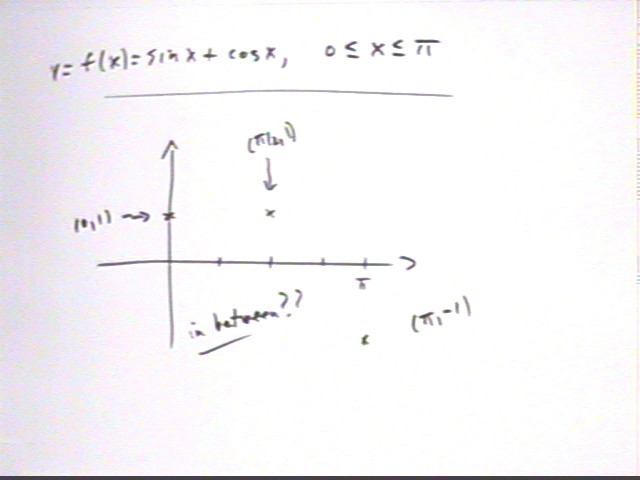
Find the maximum of f(x) = sin(x) + cos(x) for 0 < x < pi.
Our initial graph shows that f(x) has value 1 at x = 0 and x = pi/2, and value -1 at x = pi. We will investigate derivatives to see what happens between these points.
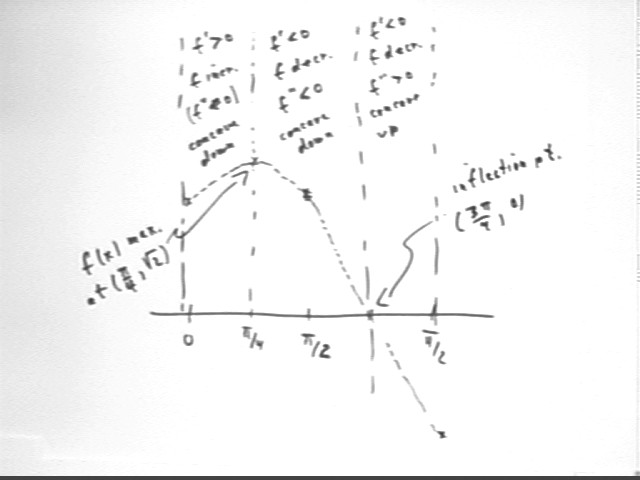
The derivative is f ' (x) = cos x - sin x. f ' (x) = 0 when cos (x) - sin(x); consideration of the unit circle shows that the cosine decreases from 1 to 0 as x goes from 0 to pi/2, while over the same x interval the sine goes from 0 to 1. Since both functions are continuous tthe two must therefore have an equal value at some x betwen 0 and pi/2. We easily see that this occurs at the 'halfway' point x = pi/4, where the symmetry guarantees the equality of the sine and the cosine.
The same model also shows us how the value of f ' (x) goes from positive to negative at x = pi/4, so that the graph of f(x) goes from increasing to decreasing at this point and therefore attains a maximum at x = pi/4. We easily find that at x = pi/4 the value of f(x) = sin x + cos x is sqrt(2)/2 + sqrt(2)/2 = sqrt(2) = 1.414, approx..
The second-derivative function f '' (x) = -sin x - cos x is seen to be zero at x = 3 pi /4, negative between x = 0 and 3 pi / 4 and positive between x = 3 pi/4 and x = pi. The graph of f(x) is therefore concave down from x = 0 to x = 3 pi / 4 and concave up from x = 3 pi / 4 to x = pi.

The construction of the graph of f(x) is summarized below.
An accurate graph of f ' (x) and f(x) is depicted below. The vertical segments are at x = 0, pi/4, pi/2, 3 pi/4 and pi.
We note
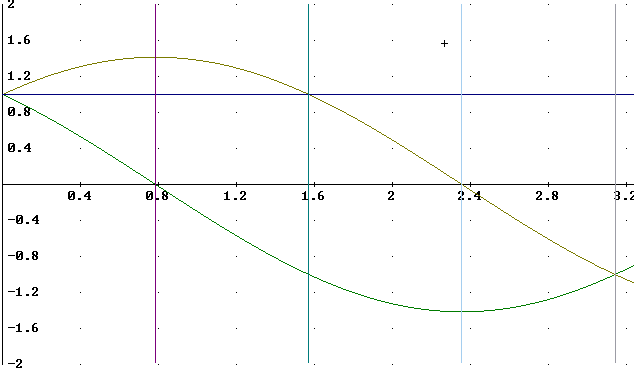
Problem Number 1
Use the Chain Rule and the derivative of f(z) = sin(z) to find the formula for the derivative of y = sin^-1(x).
Letting g(x) = sin^-1(x) we have f(g(x)) = sin(sin^-1(x)) = x so that f(g(x)) ' = x ' = 1.
Since f(g(x)) ' = g ' (x) * f ' (g(x)) we have a 'lever' with which to find g ' (x).
f ' (z) = cos(z) so we have
g ' (x) * cos (sin^-1(x) ) = 1.
sin^-1(x) is angle of a triangle with 'vertical' side x and r = 1. The 'horizontal' side is sqrt(1 - x^2) so the cosine of this angle is sqrt(1 - x^2) / 1 = sqrt(1 - x^2).
Thus g ' (x) * sqrt(1 - x^2) = 1 and
g ' (x) = 1 / sqrt(1 - x^2).
Thus (sin^-1(x) ) ' = 1 / sqrt(1 - x^2).
Problem Number 2Find the derivative of y = 5 cos (-8 `pi e^(-6 x) ) ).
This is a composite of a composite. The derivative of e^(-6x) is -6 e^(-6x).
So if we let g(x) = -8 pi e^(-6x) we have g ' (x) = 48 pi e^(-6x).
Our 'outer' function is f(z) = 5 cos(z) with f ' (z) = - 5 sin(z) so that
f(g(x)) ' = g' (x) * f ' (g(x)) =
48 pi e^(-6x) * [ -5 sin(-8 pi e^(-6x)) ] =
-240 pi e^(-6x) sin(-8 pi e^(-6x)).
Problem Number 3Make a table of left- and right-hand sums for 2, 4 and 10 subdivisions to approximate the integral int( 3 x^2 cos^2( .14x), x, 1.749429, 8.657429) (meaning the integral of 3 * x^2 cos^2( .14 x) from x= 1.749429 to x= 8.657429).
The interval from x = 1.75 to x = 8.66 has length 8.66 - 1.75 = 6.91.
If we divide the interval into, say, 4 subdivisions each will have length 6.91 / 4 = 1.73 approx. so our partition points will be
x = 1.75,
x = 1.75 + 1.73 = 3.48
x = 1.75 + 2 * 1.73 = 5.21
x = 1.75 + 3 * 1.73 = 6.94 and
x = 8.66.
We will construct a standard graph with this partition and do what comes naturally.
Problem Number 4
Water is flowing at a constant rate into an urn which is narrow at the bottom, narrow in the middle and very narrow at the top, but fat about 1/3 of the way up and very fat about 2/3 of the way up. Sketch the urn, and sketch a possible graph of depth vs. clock time and indicate on your graph when the water level is at the point where the urn is narrowest and at the point where where it is widest.
Problem Number 5
The average value of f(x) = A x^2 between x = 3 and x = 8 is 12. What is the value of A?
Problem Number 6Give the equations of the tangent lines to y = 1 - cos(-2.501 x) and y = 2 x at x = 0.
In terms of two simple examples involving temperature, rate of temperature change and time, explain the difference between the meaning of the slope of a trapezoid and the area of a trapezoid. Be sure to explain your results in terms of units and also in terms of meanings.
In terms of two simple examples involving depth, rate of depth change and time, explain the difference between a situation where you obtain a meaningful result by subtracting two quantities and dividing by a time interval and a situation where you obtain a meaningful result by averaging two quantities and multiplying by a time interval. Be sure to explain your results in terms of units and also in terms of meanings.
Problem Number 8Problem: The quadratic depth vs. clock time model corresponding to depths of 65.66846 cm, 59.55088 cm and 55.64727 cm at clock times t = 7.260405, 14.52081 and 21.78122 seconds is depth(t) = .021 t2 + -1.3 t + 74.
Problem: The depth function depth(t) = .021 t2 + -1.3 t + 74 corresponds to depths of 65.66846 cm, 59.55088 cm and 55.64727 cm at clock times t = 7.260405, 14.52081 and 21.78122 seconds.