Calculus I Quiz 1128
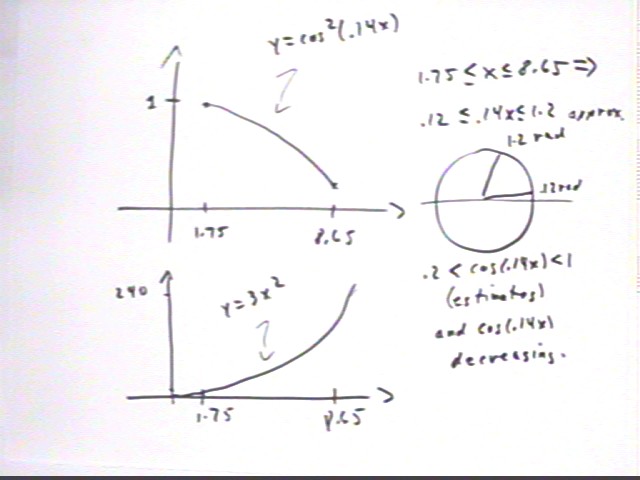
Problem Number 3Make a table of left- and right-hand sums for 2, 4 and 10 subdivisions to approximate the integral int( 3 x^2 cos^2( .14x), x, 1.749429, 8.657429) (meaning the integral of 3 * x^2 cos^2( .14 x) from x= 1.749429 to x= 8.657429).
We first construct a graph of the function. For .175 < x < 8.65 we have .2 < .14 x < 1.2, approx. so that cos(.14 x) should decrease from near 1 to about .2 or so; cos^2(x) will decrease from a bit less than 1 to a small value. In the meantime 3x^2 increases from around 8 to around 240, using ballpark estimates.
The effects of increasing values of 3 x^2 and decreasing values of cos^2(x) give us a graph with a relative maximum somewhere between x = 1.75 and x = 8.65, as depicted below.

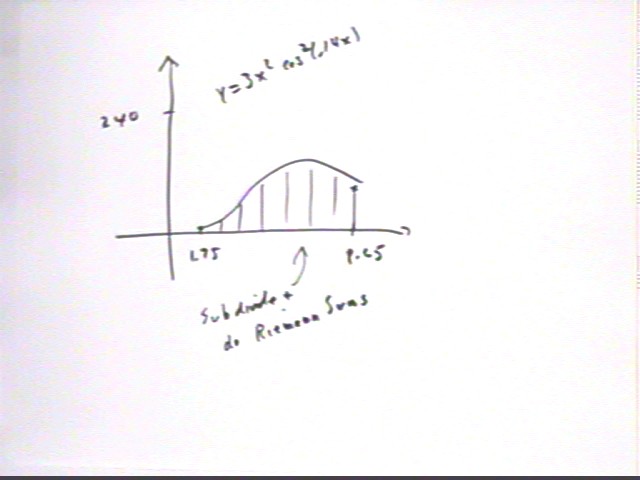
We will subdivide this graph and form the Riemann Sums.
The actual graph is shown:
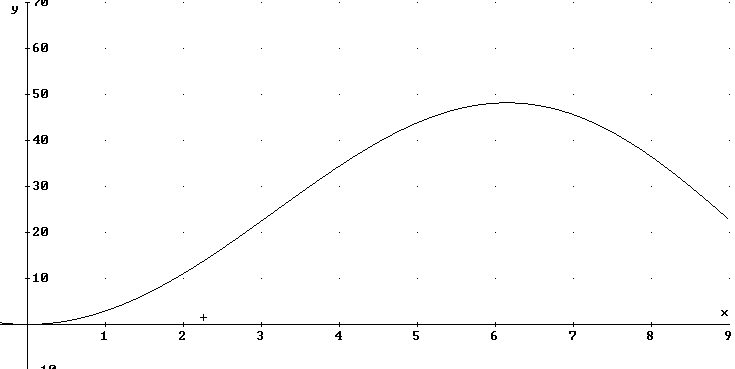
The interval from x = 1.75 to x = 8.66 has length 8.66 - 1.75 = 6.91.
If we divide the interval into, say, 4 subdivisions each will have length 6.91 / 4 = 1.73 approx. so our partition points will be
x = 1.75,
x = 1.75 + 1.73 = 3.48
x = 1.75 + 2 * 1.73 = 5.21
x = 1.75 + 3 * 1.73 = 6.94 and
x = 8.66.
We will construct a standard graph with this partition and do what comes naturally.
Proceeding with the Riemann Sums:
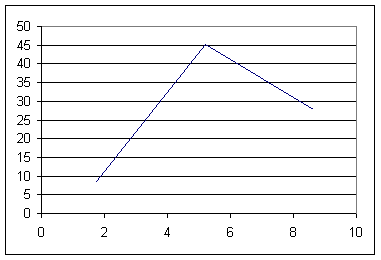
The subdivision into two intervals is shown below.
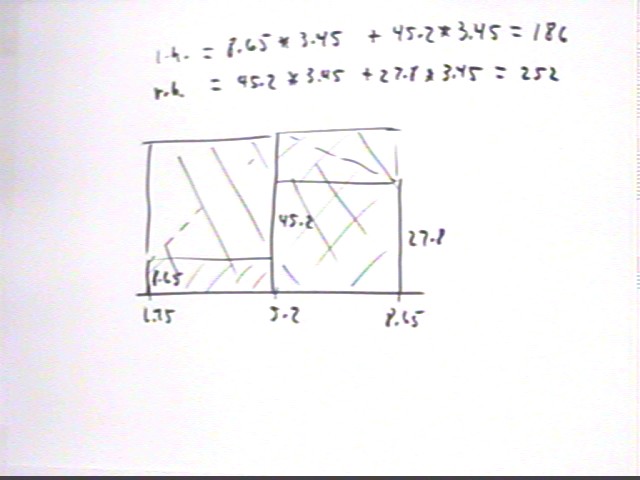
The table below gives x and y values and LH and RH 'areas' for the Riemann approximations. We see that the integral is 'squeezed' between 186 and 252; our trapezoidal approx. will be (186 + 252) / 2 = 219.
| x | y | LH | RH |
| 1.75 | 8.65 | 29.8 | |
| 5.2 | 45.2 | 156 | 156 |
| 8.65 | 27.8 | 96 | |
| 186 | 252 |
The graph below depicts the 2-interval approximation.
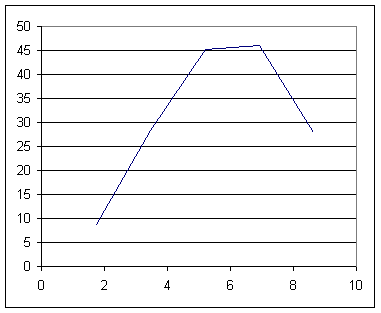
The table and graph for the 4-interval approximation are given below.
We see that the integral is now 'squeezed' between 221 and 254. Our trapezoidal approx. will be (221 + 254) / 2 = 237.5.
| LH | RH | ||
| 1.75 | 8.65 | 14.9 | |
| 3.48 | 28.3 | 48.8 | 48.8 |
| 5.2 | 45.2 | 78 | 78 |
| 6.93 | 46 | 79.4 | 79.4 |
| 8.65 | 27.8 | 48 | |
| 221 | 254 |
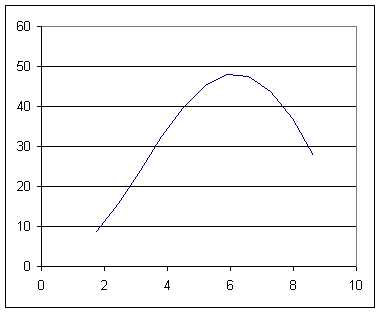
The table and graph for the 10-interval approximation are given below.
We see that the integral is now 'squeezed' between 236 and 249. Our trapezoidal approx. will be (236 + 249) / 2 = 242.5.
| LH | RH | ||
| 1.75 | 8.65 | 5.97 | |
| 2.44 | 15.9 | 10.9 | 10.9 |
| 3.13 | 24.1 | 16.6 | 16.6 |
| 3.82 | 32.4 | 22.4 | 22.4 |
| 4.51 | 39.8 | 27.4 | 27.4 |
| 5.2 | 45.2 | 31.2 | 31.2 |
| 5.89 | 48 | 33.1 | 33.1 |
| 6.58 | 47.5 | 32.8 | 32.8 |
| 7.27 | 43.7 | 30.2 | 30.2 |
| 7.96 | 36.9 | 25.5 | 25.5 |
| 8.65 | 27.8 | 19.2 | |
| 236 | 249 |
The actual value of the integral is 243.83, so we see that we approach to within 24.83, then 6.33, then 1.33 of the actual value with 2-, 4- and 10-interval approximations.
Note that 6.33 is close to 1/4 of 24.83; by doubling the number of intervals the accuracy of the trap approx. improves by a factor of 2^2 = 4.
Also 1.33 is about 1/5 of 6.33. By increasing the number of approximations by a factor of 10/4 = 2.5 our accuracy increased by a factor close to 2.5^2 = 6.25 (5 times better is close to 6.25 times better).
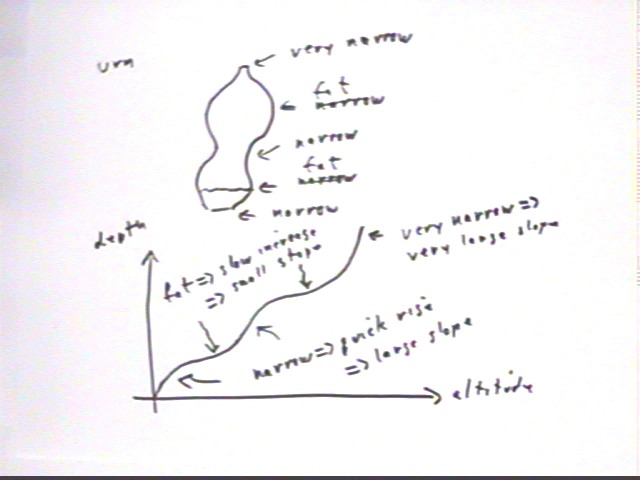
Problem Number 4Water is flowing at a constant rate into an urn which is narrow at the bottom, narrow in the middle and very narrow at the top, but fat about 1/3 of the way up and very fat about 2/3 of the way up. Sketch the urn, and sketch a possible graph of depth vs. clock time and indicate on your graph when the water level is at the point where the urn is narrowest and at the point where where it is widest.
Since water enters at a constant rate the depth will increase most quickly where the urn is narrowest and most slowly where the urn is widest. The graph is as indicated below:
The average value of f(x) = A x^2 between x = 3 and x = 8 is 12. What is the value of A?
The integral of a function over an interval is equal to its average value multiplied by the length of the interval.
The average value of a function is therefore equal to its integral divided by the length of the interval of integration.
The integral of f(x) = A x^2 between x = 3 and x = 8 is equal to the difference in the 'change-in-amount' function F(x) = A x^3 / 3. This difference is F(8) - F(3) = A * 8^3 / 3 - A * 3^3 / 3 = 485 / 3 * A.
The average value of the function is therefore
ave val = integral / interval = 485/3 * A / (8-3) = 97/3 * A.
ave val is also 12 so
97/3 * A = 12 and
A = 3/97 * 12 = 36/97.
Problem Number 6Give the equations of the tangent lines to y = 1 - cos(-2.501 x) and y = 2 x at x = 0.
First note that these functions have the point (0,0) in common, as we can see by evaluating both at x = 0.
If y = cos(-2.5 x) then y ' = -2.5 * (-sin(-2.5 x) ) = 2.5 sin(-2.5 x). At x = 0 we find that y ' = 2.5 * sin(0) = 0 so the first tangent line is just y - 0 = 0 ( x - 0) or just y = 0.
y = 2x is its own tangent line at (0, 0).
For any very small x we have (1 - cos(-2.5 x) ) / (2 x) very close to the ratio of the tangent-line approximations, which in this case is 0 / (2 x) = 0.
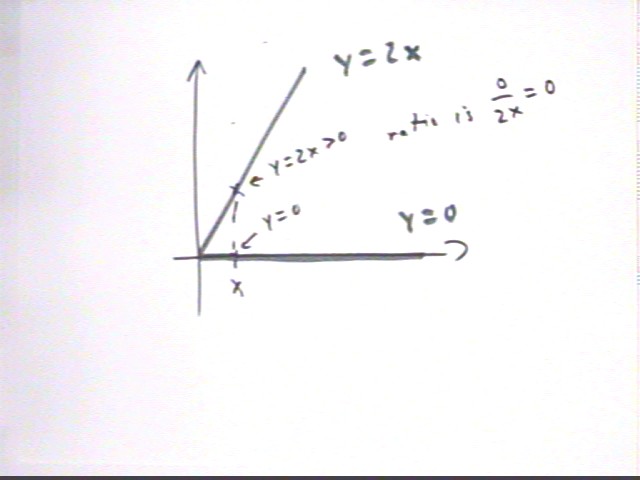
l'Hopital's Rule applies because both functions are continuous, differentiable and approach 0 and x = 0.
Thus the limiting value of the ratio is the same as the limiting value of the ratio of the derivatives, which is
lim{x ->0}( 2.5 sin(-2.5 x) / ( 2 ) ) = lim{x -> 0} (2.5 sin(-2.5 x) / [ lim{x -> 0} ( 2 ) ] = 0 / 2 = 0.
Note that the two limits are the two slopes of the tangent lines, which dictated the tangent-line solution to this problem. Thus l'Hopital's Rule is just another expression of what we learn from the tangent-line approximation.
Problem Number 7In terms of two simple examples involving temperature, rate of temperature change and time, explain the difference between the meaning of the slope of a trapezoid and the area of a trapezoid. Be sure to explain your results in terms of units and also in terms of meanings.
In terms of two simple examples involving depth, rate of depth change and time, explain the difference between a situation where you obtain a meaningful result by subtracting two quantities and dividing by a time interval and a situation where you obtain a meaningful result by averaging two quantities and multiplying by a time interval. Be sure to explain your results in terms of units and also in terms of meanings.
Refer to previous examples of such questions, which are numerous.
Problem Number 8Problem: The quadratic depth vs. clock time model corresponding to depths of 65.66846 cm, 59.55088 cm and 55.64727 cm at clock times t = 7.260405, 14.52081 and 21.78122 seconds is depth(t) = .021 t2 + -1.3 t + 74.
Problem: The depth function depth(t) = .021 t2 + -1.3 t + 74 corresponds to depths of 65.66846 cm, 59.55088 cm and 55.64727 cm at clock times t = 7.260405, 14.52081 and 21.78122 seconds.
Refer to previous examples of such questions, which are numerous.
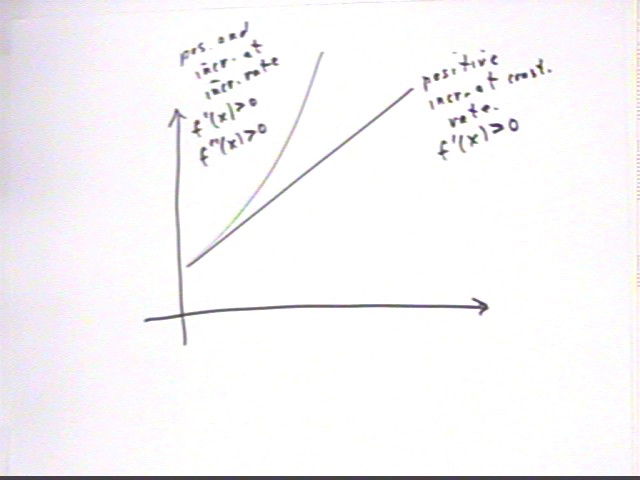
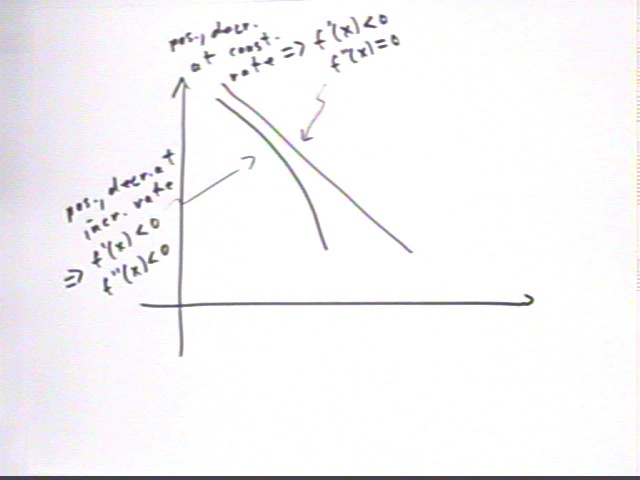
Problem Number 9What are the signs of f(x) and f ' (x) if the function f is positive and decreasing at an increasing rate? Sketch possible graphs of f(x) and f ' (x).
The figures below give examples of this sort of terminology. One of the functions shown has these characteristics. The figures also indicate the signs of f '' ( x), which weren't requested here but which could well be requested on other problems.
Explain the difference between a situation in which you would do each of the following; if there is no such situation for a given item tell why:
You would get the average value of a quantity or the average value of a rate, depending on whether y(t) corresponds to a quantity function or a rate function.
There is usually no point in dividing the average value of a quantity by the time interval.
There is usually no point in dividing the average value of a rate by the time interval.
There is usually no point in multiplying the average value of a quantity, as opposed to a rate, by the time interval.
If we multiply the average value of a rate by the corresponding time interval we get the change in value of the quantity.
The difference in two y values is the change in whatever is represented by y. Dividing the change in y be the change in t gives you the average rate of change of y with respect to t.
There is usually no point in multiplying the change in a quantity or rate by the time interval.
Problem Number 11Write the differential equation expressing the hypothesis that the rate of change of an investment is proportional to the principal P. Evaluate the proportionality constant if it is known that the when the principal is 2555 its rate of change is 300. If this is the t=0 value of the principal, then approximately what will be the principal at t = 1.9? What then will be the principal at t = 3.8?
The value of the investment would be the principle. The rate of change of investment is dP / dt. So the equation would be
dP/dt = k * P.
Thus k = (dP/dt) / P = 300 / (2555) = .12 approx.
So the equation is dP/dt = .12 * P, approx..
If P = 2555 when t = 0 then at t = 0 we have
dP/dt = k * P = .12 * 2555 = 300 approx.
so between t = 0 and t = 1.9 we have `dt = 1.9 and `dP will be
`dP = dP/dt * `dt, approx. and
`dP = 300 * 1.9 = 570, approx.
Thus new P is old P + change in P = 2555 + 570 = 3125.
So now dP/dt = .12 * P =.12 * 3125 = 375.
Between t = 1.9 and t = 3.8 we have `dt = 1.9 so that
`dP = dP/dt * `dt, approx., gives us
`dP = 375 * 1.9 = 700 approx. and we have
new P = 3175 + 700 = 3875 approx.
Problem Number 5
Explain why the derivative of an even function is an odd function.
Problem Number 6Solve using proportionalities by stating the appropriate proportionality law and finding the proportionality constant:
The rate at which a certain quantity grows is rate = 8 * log( .14 t + 1), where the rate is in units / hour and t is clock time in hours. Use two 2-interval approximations to estimate the change in velocity between clock times t = 2.2 hours and t = 7.37 hours. One of your approximations should be an overestimate, the other an underestimate.