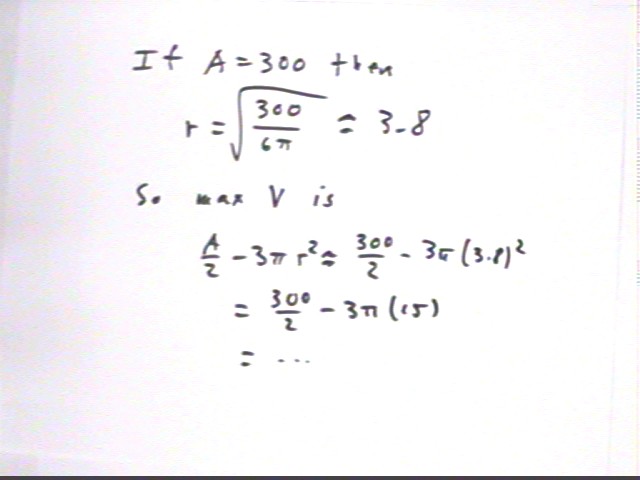
Calculus I Quiz 1206
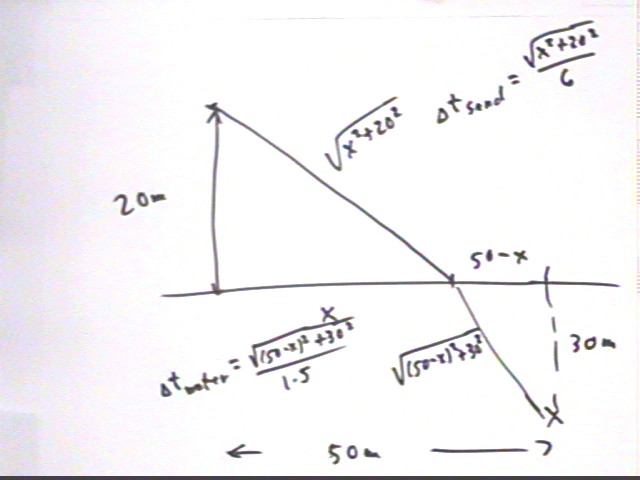
The shore of a beach runs due North and South. A lifeguard can run across the sand at 6 meters / second, and can swim through the water at 1.5 meters / second. The lifeguard is 20 meters due West of the shore and a swimmer is in trouble 50 meters to the North and 30 meters to the East of the shore.
The lifeguard will run along the hypotenuse of a triangle with legs 20 m and 30 m (see below for a general depiction of this situation when the distance is x), then swim along the hypotenuse of a triangle with legs 30 m and 20 m.
Running distance is therefore sqrt(30 ^2 + 20 ^ 2) meters. At 6 m/s the time required is therefore
Running distance is sqrt(20 ^2 + 30 ^ 2) meters. At 1.5 m/s the time required is therefore
for a total time of 6 sec + 24 sec = 30 sec.
The lifeguard will run along the hypotenuse of a triangle with legs 20 m and 40 m (see below for a general depiction of this situation when the distance is x), then swim along the hypotenuse of a triangle with legs 30 m and 10 m.
Running distance is therefore sqrt(40 ^2 + 20 ^ 2) meters. At 6 m/s the time required is therefore
Running distance is sqrt(10 ^2 + 30 ^ 2) meters. At 1.5 m/s the time required is therefore
for a total time of 7.45 sec + 21.1 sec = 28.55 sec.
This is an improvement over the 30 sec time previously obtained.
The lifeguard will run along the hypotenuse of a triangle with legs 20 m and 50 m (see below for a general depiction of this situation when the distance is x), then swim straight out for a distance of 30 m.
Running distance is therefore sqrt(50 ^2 + 20 ^ 2) meters. At 6 m/s the time required is therefore
Running distance is 30 meters. At 1.5 m/s the time required is therefore
for a total time of 9 sec + 29 sec = 29 sec, a bit slower than the preceding calculation.
We conclude that there is an optimal position x North of the starting point, somewhere between x = 30 m and x = 50 m, at which to enter the water.
If the lifeguard runs straight to a point on the shore which is x meters to the North then swims directly to the swimmer how long will it take to reach the swimmer?
Entering the water distance x North of the starting point the lifeguard will run along the hypotenuse of a triangle with legs 20 m and x m (see below for a general depiction of this situation when the distance is x), then swim along the hypotenuse of a triangle with legs (50 - x) m and 30 m.
Running distance is therefore sqrt(x ^2 + 20 ^ 2) meters. At 6 m/s the time required is therefore
Running distance is sqrt((50-x) ^2 + 30 ^ 2) meters. At 1.5 m/s the time required is therefore
for a total time of 9 sec + 29 sec = 29 sec, a bit slower than the preceding calculation.

What distance x gets the lifeguard to the swimmer in minimum time?
Letting T(x) be the total time
we minimize T(x) using the standard procedure (find critical points, etc.)
We obtain T ' (x) as depicted below (the radicals in the denominator aren't filled in but it should be clear what they represent).

Wishing to minimize T we set T ' (x) equal to 0. The equation we obtain is pretty messy to solve; the solution requires us to square both sides, which will still leave us with radicals, then isolate these radicals on one side and square again. The process works and gives us approximate solution
x = 43.02 m,
which was obtained using a computer algebra program so as not to get bogged down in algebraic details.
We can verify that T ' (x) changes from negative to positive at x = 43.02, or we can find T ''(x) and verify that the second derivative is positive at x = 43.02.
This proves that the minimum is T(43.02) = 28.44, corresponding to 28.44 second. Note that this is a slight improvement over the 28.55 s time obtained for x = 40 m.

A cylindrical can with top, bottom and sides has total area 300 cm^2.
If the radius is 2 cm then
Does it seem that there will be a radius which will maximize the volume?
What is the exact radius at which volume is maximized?