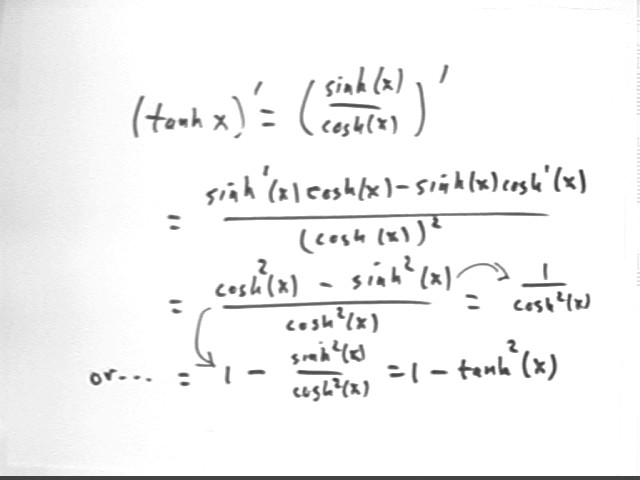
Calculus I Quiz 1209
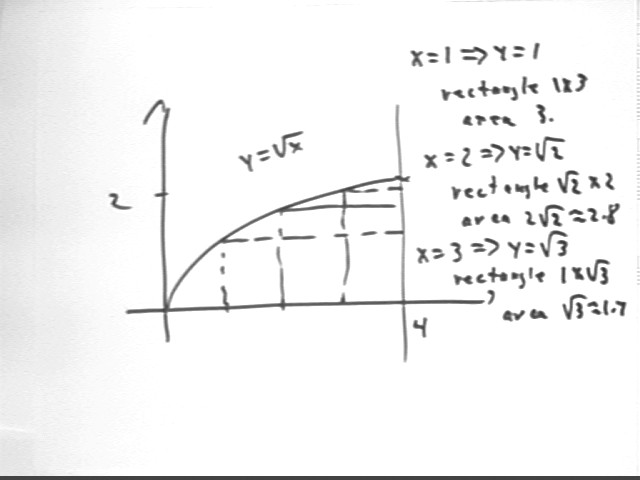
Sketch the curve y = sqrt(x) for 0 < x < 16.
Construct a rectangle by sketching a vertical line from the point (.5,0) to the curve, then right to the vertical line x = 16. What is the area of this rectangle?
At x = .5 we have sqrt(x) = sqrt(.5) =.71 approx.
The rectangle has altitude .71 and extends from x = .5 to x = 4.
Area is therefore .71 ( 3.5) = 2.5 approx.
Repeat for the point (1, 0).
Dimensions 1 x 3, area 3.
Repeat for the point (2, 0).
Dimensions sqrt(2) x 2, area 2 sqrt(2) = 2.8 approx..
Repeat for the point (3, 0).
Dimensions sqrt(3) x 1, area sqrt(3) = 1.7 approx..
These dimensions and areas are summarized in the picture below.
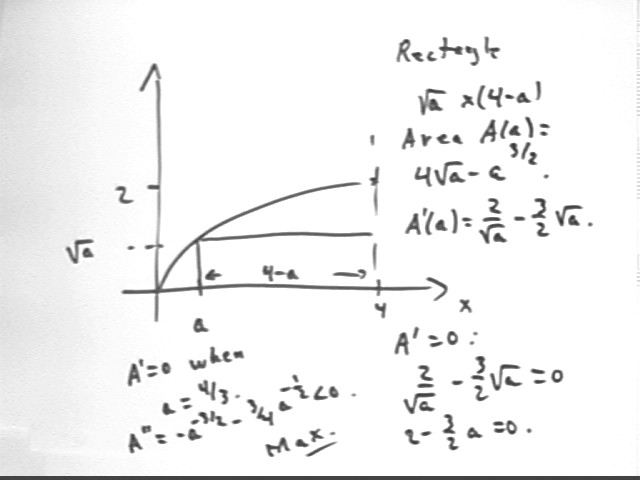
Repeat for the point (a, 0). What value of a maximizes the area of the rectangle?
As shown in the figure below we find that:
It follows that the area is maximized for a = 4/3.

The functions sinh(x) and cosh(x) are defined as follows:
Show that the derivative of sinh(x) is equal to cosh(x), while the derivative of cosh(x) is equal to the derivative of sinh(x).
[ sinh(x) ] ' = [ (e^x - e^-x) / 2 ] ' = 1/2 (e^x - e^-x) ' = 1/2 (e^x + e^-x) = (e^x + e^-x) / 2 = cosh x.
[ cosh(x) ] ' = [ (e^x + e^-x) / 2 ] ' = 1/2 (e^x + e^-x) ' = 1/2 (e^x - e^-x) = (e^x - e^-x) / 2 = sinh x.
If tanh(x) = sinh(x) / cosh(x) then what is the derivative of tanh(x)?
We easily find the derivative using the quotient rule. The derivative is found in the figure below.
We note that the identity cosh^2(x) - sinh^2(x) = 1, which is somewhat analogous to the identity cos^2(x) + sin^2(x) = 1, is easily proven from the definitions of the cosh and sinh functions.
There are two forms in which the derivative of tanh(x) can be expressed. One is 1 / cosh^2(x), the other is 1 - tanh^2(x).