
Calculus I Quiz 1211
Suppose that you rent a car for $5 / hour and that you also pay for the gas you use. Gas usage 1 gal + 2 gal * (v / 50)^2 per hour. If gas costs $1.50 / gallon how fast should you go to minimize the cost per mile? How does your answer change if the price of gas drops to $1 / gallon? What if the price is $2 / gallon?
We can easily find the cost per hour: We get 5 + 1.50 (1 + 2 ( v / 50)^2) dollars / hr when v is in mph.
To get cost per mile we divide cost per hour by miles per hour. We justify this as follows:
Dividing cost per hr by speed we have

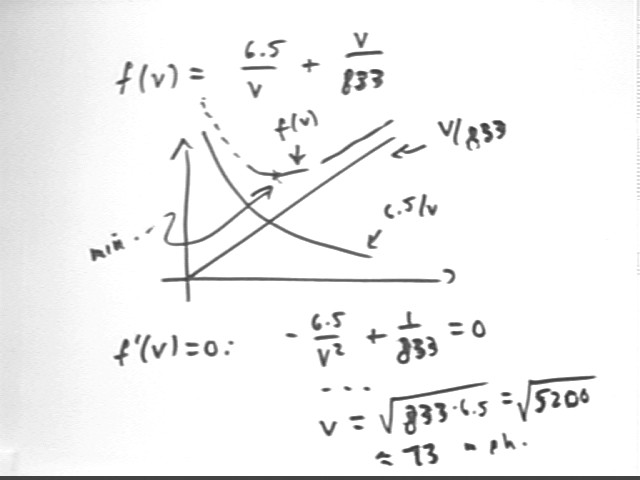
Simplifying this expression we get the cost-per-mile function f(v) = 6.5 / v + v / 833.
We construct a graph of this function. y = 6.5 / v and the linear y = v / 833 are familiar functions; they have graphs with the indicated shapes. y = 6.5 / v has a vertical asymptote at v = 0 and approaches the horizontal axis as v increses; y = v / 833 increases at a constant rate. Adding these two functions gives a function which has a vertical asymptote at v = 0 and approaches the linear y = v / 833 as v gets large.
It is easy to see that a continuous function with these characteristics must have a global minimum.
We easily find the minimum. We easily find that f ' (v) = -6.5 / v^2 + 1 / 833. Setting f ' (v) = 0 we find that v = 73 approx., indicating a critical point at velocity 73 mph.
Noting that f '' (v) = 13 / v^3 is positive for all positive v we conclude that the critical point does give us a minimum.
So according to this model, when gasoline costs $1.50 / gal we minimize per-mile consumption at v = 73 mph. This is not an excuse, of course, for breaking the speed limit. Even if the model was valid for your vehicle, which is almost certainly is not, the speed limit is as it is.
We could repeat this analysis for costs of $2 / gal and $1 / gal. However we will find it both more efficient and more instructive if we just use c for the cost / gal. In this case our function becomes
f(v) = [ 5 + c ( 1 + 2 v^2 / 2500) ] / v = ( 5 + c) / v + 2 c v / 2500 = ( 5 + c) / v + c v / 1250.
We easily find f ' (v) and solve the equation f ' (v) = 0, obtaining min per-mile cost at v = sqrt(1250 ( 5 + c) / v).
To investigate how this function changes for different values of c we rewrite this as
v = 35 sqrt( (5 + c) / c) ).
We see that when c is very large, sqrt((5 + c) / c) approaches 1 so that for very high gasoline costs our per-mile cost is minimized at v = 35 mph.

To more rigorously analyze this behavior we take the limit as c -> infinity of the expression. In the form v = 35 sqrt( 5 / c + 1) it is even more clear that for large c the value of v will be near 35.
We note that plugging in 1.5 for c gives us the same result (74 mph here, within mental approximation the same as the 73 mph we estimated earlier) as previously.
If c = 2, corresponding to $2 / gal, we see that our minimizing velocity decreases to around 66 mph.
If c = 1 we get v = 85 mph approx..
Note that as c -> 0 the minimizing velocity approaches infinity. This is consistent with the idea that if fuel is free but it still costs $5 / hr to run the vehicle, we get the lowest per-mile cost by running as fast as possible. This also reveals a weakness of the model, because at high speeds wear and tear on the car will increase and our hourly cost won't remain at $5 / hr.
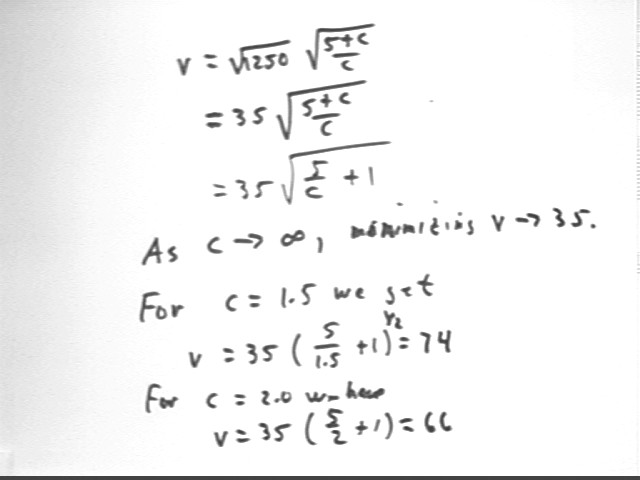
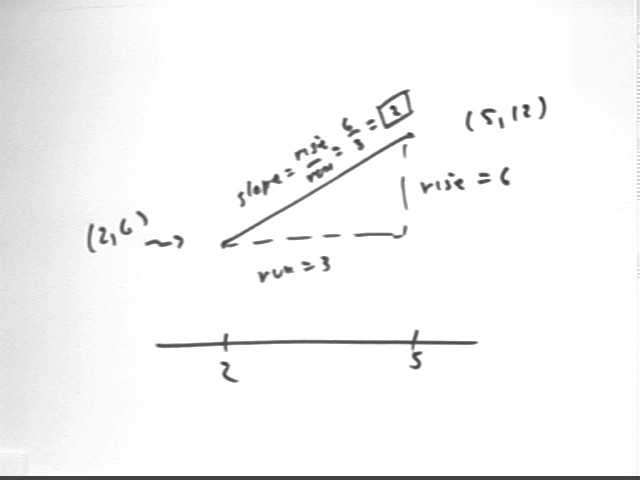
If for the function y = f(x) we know that f(2) = 6 and f(5) = 12 then what is the average rate of change of f with respect to x on the interval [ 2, 5 ] ?
The average rate of change is `dy / `dx = (12 - 6) / (5 - 2) = 6 / 3 = 2.
Sketch a graph depicting these points and the average rate of change.
The graph shows points (2, 6) and (5, 12), with the slope segment running from one point to the next. The rise is `dy = 6, the run is `dx = 3, the slope is rise/run = 6 / 3 = 2.
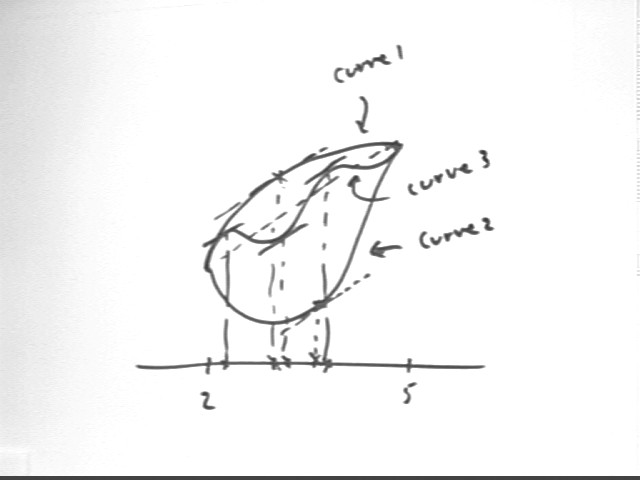
Now sketch a possible graph for f(x) which is not linear and whose derivative is continuous. Identify any point(s) on that graph for which the derivative is equal to the average rate of change on the interval.
Ave rate of change is represented by the ave slope of the straight line.
The graph below shows the two endpoints at x = 2 and x = 5, with the straight dotted line between them and in addition curves 1, 2 and 3 all going from the left endpoint to the right.
The points where slope = average slope (i.e., the straight-line slope and the slope of the tangent line) are indicated; from each of these points we project straight down to the x axis, showing the x values at which the condition holds.
We see that if a curve starts out steeper than the straight line representing the ave slope it must eventually turn back toward that line, and at some point its slope will have to match that of the line. Similar reasoning tells us that if we start out 'below' the straight line we'll have to curve back toward it and again there will be a point where our slopes are equal.
See if you can sketch a graph for a continuously differentiable f(x) for which there is no point on that graph for which the derivative is equal to the average rate of change on the interval.
Our best try might be something like the following:
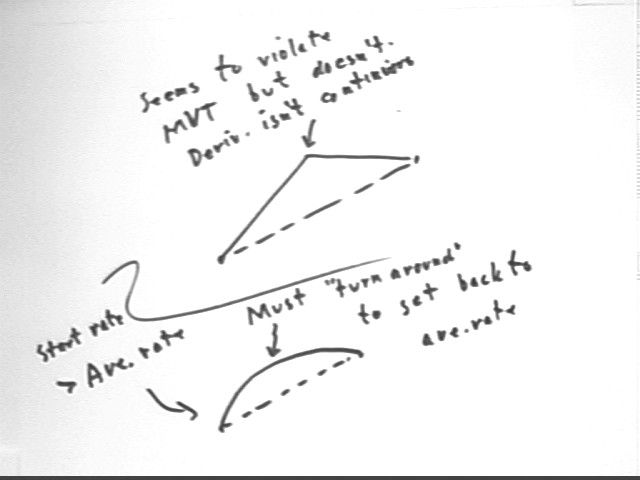
However the function depicted isn't continuously differentiable. The derivative changes instantaneously at the 'peak'.
Suppose that (a, f(a) ) is a local max for a continuous function y = f(x). Then for small h what can we say about the sign of f(a+h) - f(a)?
If f(a) is the max value then f(a+h) < f(a) and f(a+h) - f(a) < = 0.
This is true whether h is positive or negative (it doesn't matter whether a+h is to the left or to the right of a).
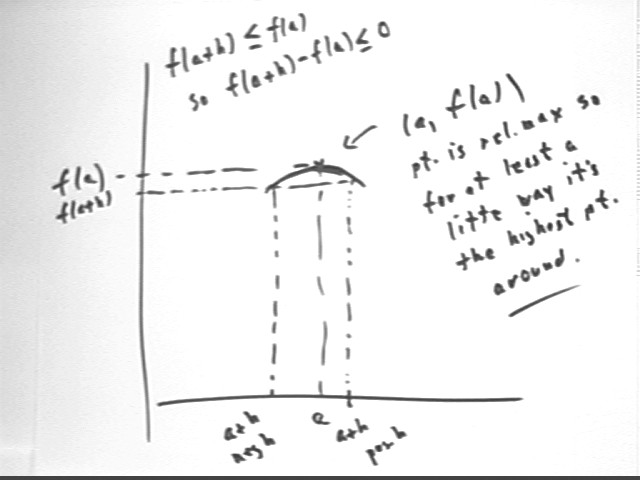
If we assume that f(a+h) - f(a) < 0 it follows that when h is positive the ratio will be negative / positive, or negative, and when h is negative the ratio will be negative / negative or positive.
If f(a+h) - f(a) = 0 then the ratio will be zero, whether h is positive or negative.
So we conclude that if h > 0 the ratio is <= 0, and if h < 0 the ratio is >= 0.
Now we note that the limiting value, as h -> 0, or the ratio [ f(a+h) - f(a) ] / h is the derivative f ' (a). We have assumed that f is differentiable at a so we know that the derivative must exist.
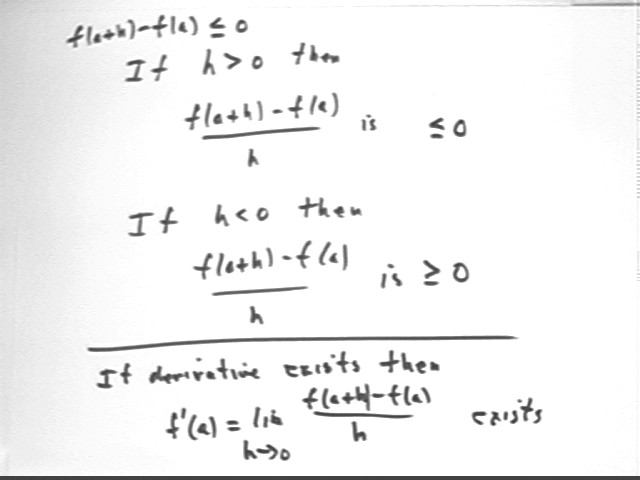
How do your answers make it inevitable that lim{h -> 0} [ f(a+h) - f(a) ] / h = 0?
If the limit exists then the left-hand and right-hand limits must exist. However the left-hand limit involves values of h < 0 so from what we saw earlier the left-hand limit is < = 0; and the right-hand limit involving values of h > 0 we know that the right-hand limit is >= 0.
The two limits must be equal, so they must both be zero.
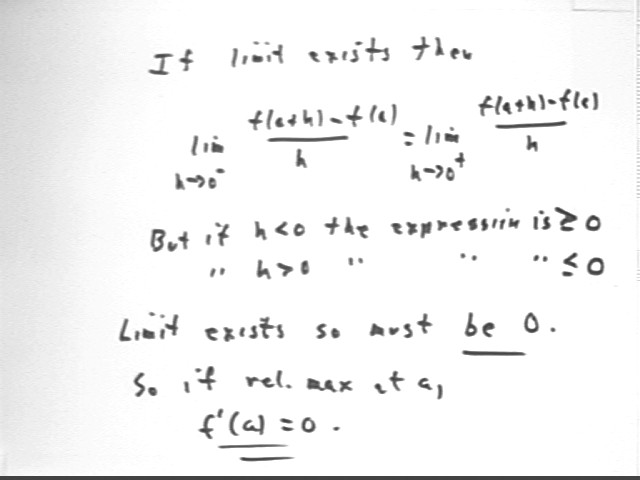
What does this tell you about the derivative of f(x) at x = a?
This tells us that the derivative of f(x) at a is f ' (a) = 0.
This proves that the derivative of a function is zero at a relative maximum. It would be as easy to prove the same for a relative minimum.