Calculus I Quiz 1213
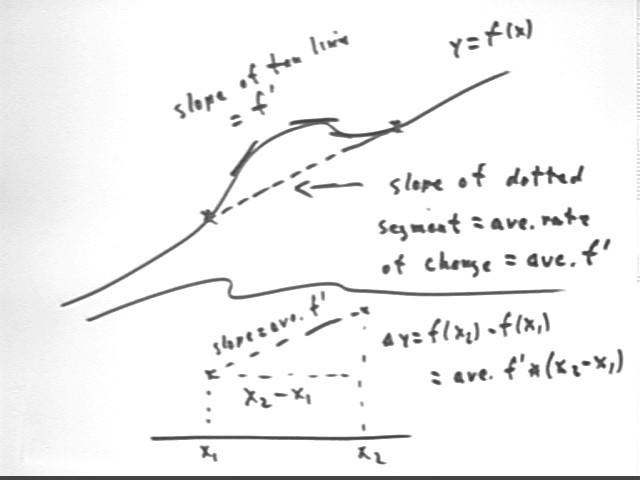
Sketch a graph to show that f(x2) - f(x1) = ( ave value of f ' ) * (x2 - x1).
A graph is depicted in the figure below. The slope of the graph of f(x) at a point represents f ' (x) at that point. The average slope between two points is the slope of the straight line segment connecting those points.
The second picture in the figure depicts how `dy = slope * run = (ave f ' ) * ( x 2 - x1). Since `dy = f(x2) - f(x1) we have
f(x2) - f(x1) = (ave f ' ) * ( x 2 - x1).

Provided x2 > x1 we have
f(x2) - f(x1) = (ave f ' ) * ( x 2 - x1) = positive quantity * positive quantity = positive quantity.
That is f(x2) - f(x1) > 0.
If f ' is never negative then ave f ' cannot be negative so ave f ' >= 0. Reasoning identical to that used previously lead to the conclusion that f(x2) - f(x1) = nonnegative quantity * positive quantity = nonnegative quantity. The possibility is open that this quantity might be 0 but it can't be negative.
Similar reasoning easily answers the remaining questions below.

Suppose that g(x) and h(x) are equal at x = a, and for a < x < b we know that g ' (x) < h ' (x).
The figure below first shows the coincident points (a, g(a)) and (a, h(a)). It seems obvious that if g ' > h ' the graph will remain steeper for all x > a.
However this requires a more rigorous proof.

The second half of the figure above indicates that since f ' = h ' - g ' and h ' > g ' we have h ' - g ' > 0, so that f ' > 0.
Since f = h - g = 0 at x = a and f ' > 0 we conclude from our reasoning on the first part of the problem that f > 0.
Thus h - g > 0 for x > a so that h > g for x > a.

Problem Number 1
What is the exact rate at which a population P(t) = 7300 * 1.18^t, t in years, is changing at the instant t = 8?
The exact rate is the derivative P ' (t) evaluated at t = 8.
P ' (t) = 7300 * ln(1.18) * 1.18^t. Evaluating we get
P ' (8) = 4500 approx..
Slope of tan line is derivative; tan line goes thru ( 8, P(8)) = (8, 27000) approx.
The tan line is therefore
y - 27000 = 4500 ( t - 8), or
y = 4500 t - 9000.
Differential approximation is `dP = P ' (t) * `dt. We're approximating at t = 8 with `dt = .001 so the approximation is `dP = P ' (8) * .001.
We thus obtain `dP = 4500 * .01 = 45 approx..
Change in P is rate of change of P with respect to t multiplied by `dt. Multiply how much t changes by how fast P changes. e.g., multiply rate of change in critters per day by number of days and you get change in number of critters.
Problem Number 2A lifeguard needs to get to a swimmer 55 meters from shore as quickly as possible. The shoreline is a straight line and the lifeguard is 45 meters from the shoreline and 100 meters in the direction of the shoreline from the swimmer. How far down the shoreline should the lifeguard enter the water if she runs at 5.7 meter / sec along the sand and swims at 1.9 meters / sec?
done very recently; skip for now except to say that we write total time as a function of distance x up the shore and minimize by setting derivative with respect to t equal to zero then checking 2d derivative to be sure it's positive.
If the lifeguard enters the water x meters along the shoreline toward the swimmer then she travels distance sqrt( (55 m)^2 + x^2) along the sand, requiring `dt1 = sqrt( (55 m)^2 + x^2) / (5.7 m/s), then sqrt( (45 m)^2 + ( 100 m - x)^2 ) in the water, requiring `dt2 = sqrt( (45 m)^2 + (100 m - x)^2) / (1.9 m/s).
Suppressing units and understanding that x will be in meters we find that the total time is
T(x) = sqrt( 55^2 + x^2) / 5.7 + sqrt(45^2 + (100-x)^2) / 1.9.
We need to minimize T(x). We find that
T ' (x) = x / (5.7 sqrt(55^2 + x^2) - (100-x) / (1.9 sqrt(45^2 + (100-x)^2).
We set T ' (x) = 0 and solve to obtain a critical point. The expression is complicated enough that we can use a graphical approximation.
T''(x) is positive at the critical point so the function is maximized at this point.
Problem Number 3
Explain the difference between a situation in which you would do each of the following; if there is no such situation for a given item tell why:
not usually meaningful
this gives ave rate of change of y with respect to t
not usually meaningful
if y is rate of change of some quantity then averaging the two y values gives an approximation to the average rate; multiplying by the difference in t values multiplies approx ave rate by time interval giving approx change in whatever quantity y is the rate of change of ...
Problem Number 4For what interval(s) is 1 / (x^2 + 4) concave down, and for what interval(s) is it concave up?
find where second derivative is positive and where negative: take 2d derivative, set equal to 0, find intervals defined by zeros and vertical asymptotes where positive and where negative.
f ' (x) = 2x / (x^2+4)^2 so
f '' (x) = [ (2x)' (x^2+4)^2 + ( (x^2+4)^2) ' * 2x ] / (x^2+4)^2 = 2·(3·x^2 - 4)/(x^2 + 4)^3.
f '' (x) = 0 when the numerator 2(3x^2 - 4) = 0. We easily solve this equation to obtain x = +- 2 sqrt(3) / 3 (around +- 1.13).
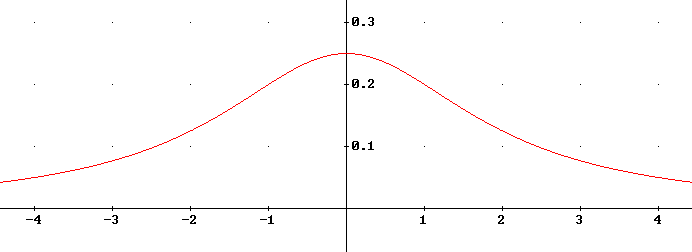
The graph of y = f(x) is depicted below. Note that the concavity does appear to change near x = 1 and x = -1.
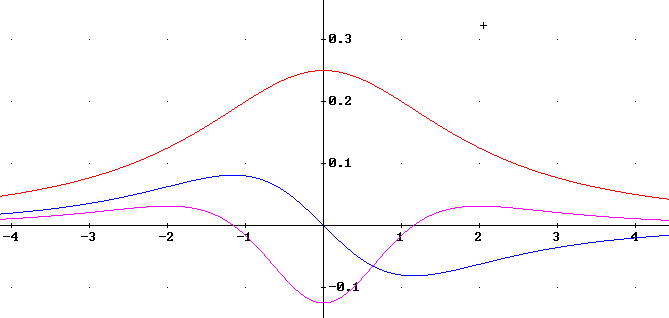
The figure below depicts the graphs of f(x), f ' (x) and f ''(x).
Problem Number 5
Solve using proportionalities by stating the appropriate proportionality law and finding the proportionality constant:
mass occupies tiny cubes so mass proportional to volume which is proportional to cube of linear dimension.
height of geom similar sandpiles is a linear dimension so m = k h^3.
Evaluate k, rewrite proportionality with this k, use the proportionality to answer questions.
similar to previous but surface occupied by tiny squares so proportionality is N = k h^2, etc.
Problem Number 6Answer by calculating an appropriate limit using l'Hopital's Rule:
For large x both ln(7x) and x^(1/15) -> infinity so l'Hopital's Rule applies for limits at infinity.
So lim {x -> infinity} ( 584 ln(7x)) / (x^(1/15) ) =
lim{x -> infinity} (( 584 ln(7x)) ' / (x^(1/15) ) ' =
lim{ x -> infinity} [ (7 * 584 / (7 x) ) / (1/15 x^(1-1/15) ) ] =
lim {x -> infinity} [ 584 * 15 / x^(1/15) ] = 0.
The final limit is zero since the denominator x^(1/15) approaches infinity as x -> infinity.
Problem Number 7Use the Chain Rule and the derivative of f(z) = sin(z) to find the formula for the derivative of y = sin^-1(x).
If z = sin^-1(x) and f(z) = sin(x) then f(z(x)) = x and (f(z(x))) ' = 1.
f(z(x)) ' = z ' (x) * f ' (z(x)) = [ sin^-1(x) ] ' * cos(sin^-1(x)) so
[ sin^-1(x) ] ' * cos(sin^-1(x)) = 1 so that
[ sin^-1(x) ] ' = 1 / cos(sin^-1(x)) = 1 / sqrt(1 - x^2).
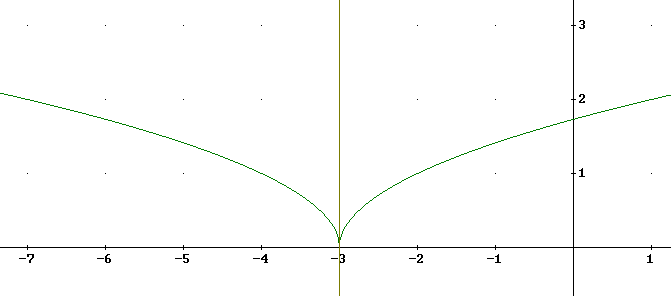
Problem Number 8Is f(x) = `sqrt | 3 + x | continuous at x = - 3? Is f(x) differentiable at this point?
Since |x + 3 | = x + 3 when x + 3 >= 0 and -(x + 3) when x + 3 < 0 we have
This is depicted int he figure below.
The right- and left- hand limits of f(x) as x -> -3 are both zero, so
lim{x -> -3} f(x) = f(-3) = 0
showing that the function is continuous.
On the other hand the derivative is
As x -> -3 we see that sqrt(x+3) -> 0 so
Thus the derivative function does not have a limiting value as x -> -3 and is not continuous at this point.
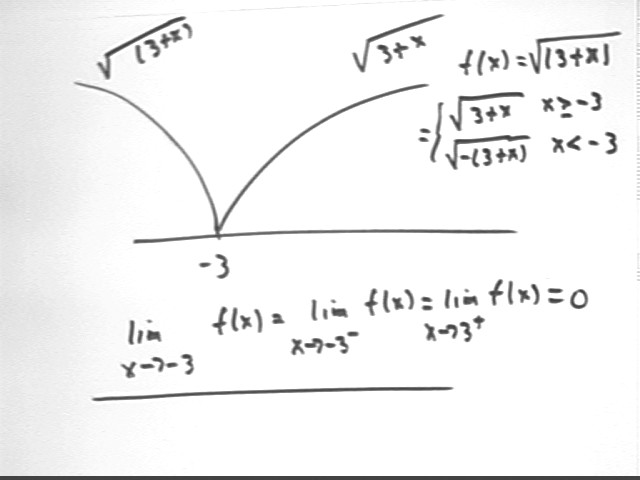
The figure below shows an accurate graph of this function, along with the vertical line x = -3 which shows how the slope is unlimited as x -> 3..
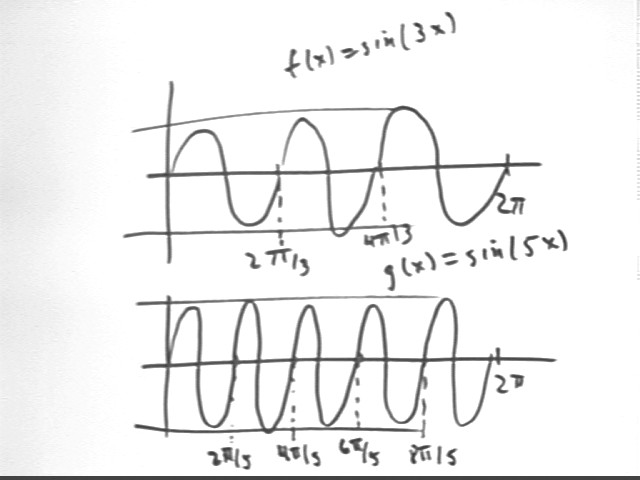
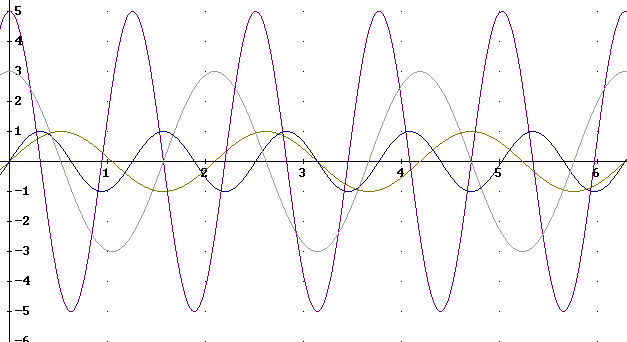
On a single set of axes graph f(x) = sin( 3 x) and g(x) = sin( 5 x) from x = 0 to x = 2 `pi. On a second set of axes graph f ' (x) and g ' (x) and compare the graphs, being careful when comparing slopes of f(x) and g(x) at each point.
The graph of sin(3x) will undergo 3 complete cycles between x = 0 and x = 2 pi. Cycles will correspond to the intervals defined by x = 0, 2 pi/3, 4 pi/3 and 2 pi.
The graph of sin(3x) will undergo 5 complete cycles between x = 0 and x = 2 pi. Cycles will correspond to the intervals defined by x = 0, 2 pi/5, 4 pi/5, 6 pi/5, 8 pi/5 and 2 pi.
These graphs are depicted below.
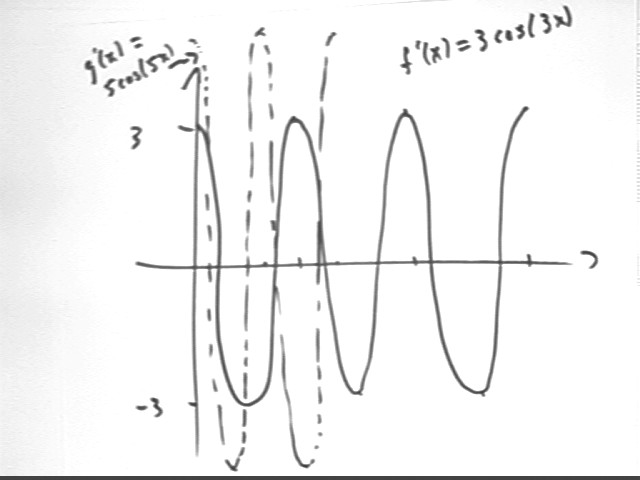
The derivatives g ' (x) = 5 cos(5x) and f '(x) = 3 cos(3x) are depicted below for the interval 0 < x < 2 pi. g ' (x) has amplitude 5 and f ' (x) has amplitude 3; the cycles run over the same intervals as those of the original functions.
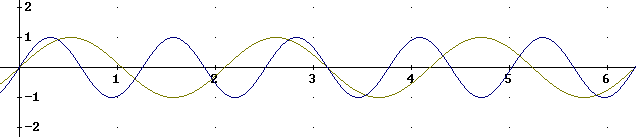
An accurate graph of f and g is depicted below, again over the interval 0 < x < 2 pi.
Graphs of f ' (x) = 3 cos(3x) and g ' (x) = 5 cos(5x) are depicted below along with the graphs of f and g.
Problem Number 10
Find the equation of the line tangent to the curve x^ 2.5 + y^ 2.5 = 1^ 2.5 at (0, 1).
Use implicit differentiation to get 2.5 x^1.5 + 2.5 y^1.5 y ' = 0 so
y ' = -x^1.5 / y^1.5 .
At x = 0 and y = 1 we have
y ' = -0 / 1 = 0.
So the tangent line at (0, 1) is just y = 1.
Problem Number 11Define tanh (x). Graph it and give its derivative. Prove from the definition of tanh(x) and from the derivatives of sinh(x) and cosh(x) that the derivative you have given is correct.
just done
Problem Number 12Make a table of left- and right-hand sums for 2, 4 and 10 subdivisions to calculate the approximate integral int( 4 sin^2( .3x) / x, x, 1.235067, 3.3284) (meaning the integral of 4 * sin^2( .3 x) from x= 1.235067 to x= 3.3284).