Calculus I Quiz 0911
Would the average of the t = 20 and t = 70 values of the rate function y ' (t) = -.01 t^2 + 2 t - 70 result in an overestimate or an underestimate of the change in y between t = 20 and t = 70?
Using standard precalculus techniques we see that a graph of y ' is concave down, meaning that between any two points the linear approximation will underestimate the rate. Since the rate is underestimated the change will be underestimated.
Approximately how much change in y would you expect to observe during a .2-second time interval near t = 70, given the above rate function? Would your approximation be an overestimate or an underestimate?
y ' (70) = 21. Using this as ave rate we get `dy = y ' * `dt = 21 * .2 = 4.2.
We don't expect that y ' will change much between t = 70 and t = 70.2 so we expect that this is probably a pretty good estimate.
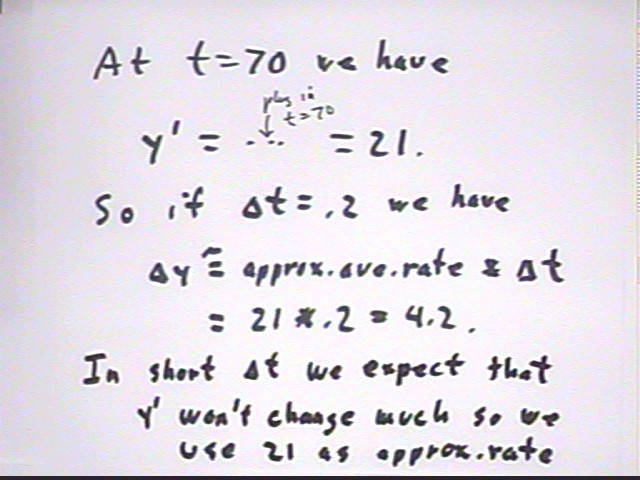
The derivative of y = e^(k t) is y ' (t) = k * e^(k t). If a temperature function was given by T(t) = e^(-.03 t) then at what rate would the temperature be changing at t = 40 and approximately how much temperature change would be expected during a 2-second interval near that time? Would your approximation be an overestimate or an underestimate?
T ' = -.03 e^(-.03 t).
At t = 40 we get T ' = -.0090 so if `dt = 2 we have
`dT = T ' `dt = -.0090 * 2 = -.018.
What would be the equation of the line tangent to the graph of T vs. t at the T = 40 point?
We easily find the t = 40 point of the graph: t = 40 and T = e^(-.03 * 40) = .302.
We also know that the derivative is -.009 so the slope of the tangent line must be -.009.
This gives us a point and slope for the tangent line and we easily find the equation to be
T - .302 = -.009 ( x - 40) or
T = -.009 x + .662.
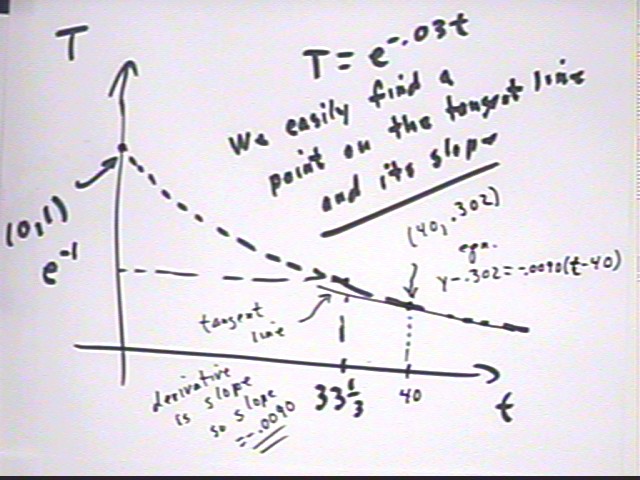
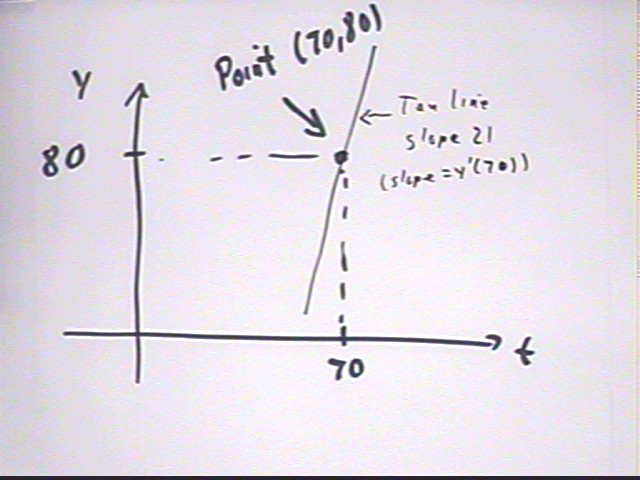
What is the equation of the tangent line to the graph of y ' (t) = -.01 t^2 _ 2 t - 70 at the t = 70 point?
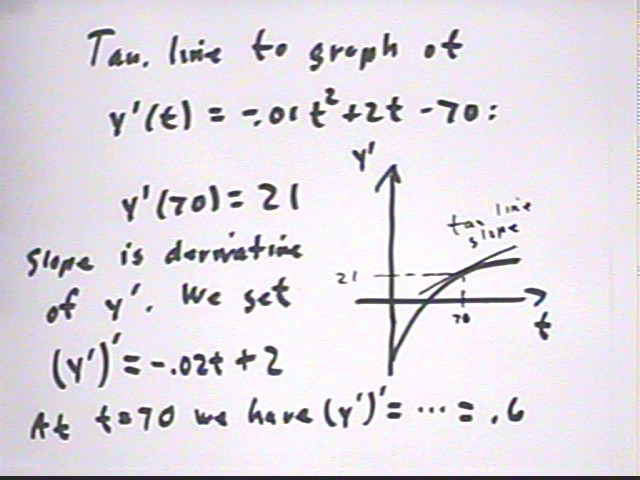
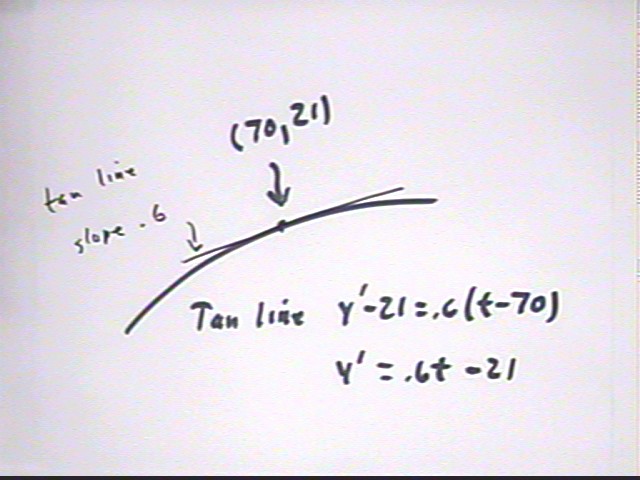Find the equation of the tangent line to the y(t) function (y
' as indicated on the quiz) at t = 70 if it is known that y(70) = 80.
The given information tells us that (70, 80) is a point on the y(t) graph.
At t = 70 we already know from before that y ' = 21.
So the slope of the tangent line is 21 and the equation is
y - 80 = 21 (t - 70) or
y = 21 t - 1390.
What are the y coordinates of the tangent line at t = 70 and at t = 70.2? How much difference is there between these values?
Evaluating y at t = 70 we get y = 80, as we better. At t = 70.2 we get y = 84.2.
The change of 4.2 in the value of y agrees with the approximation we obtained in the quiz.
That approximation is called a differential approximation or a tangent-line approximation.
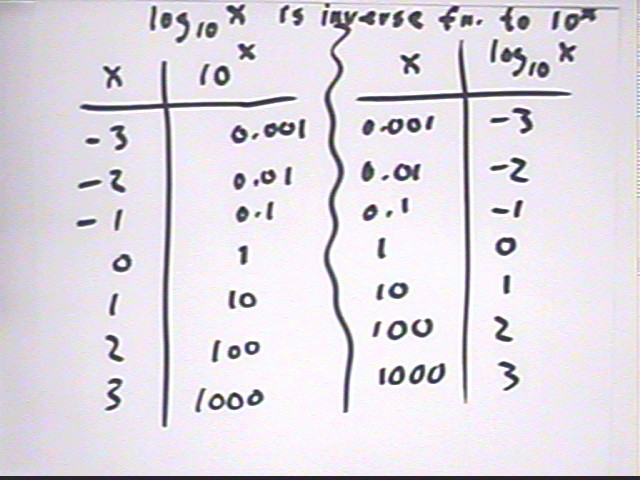
A logarithm is an inverse of an exponential function. If we reverse the columns of the partial table of the function 10^x we get a partial table for the function log{base 10} (x).
For any x we have log{base 10} ( 10^x) = x and if x > 0 we have 10^(log{base 10}(x) ) = x:
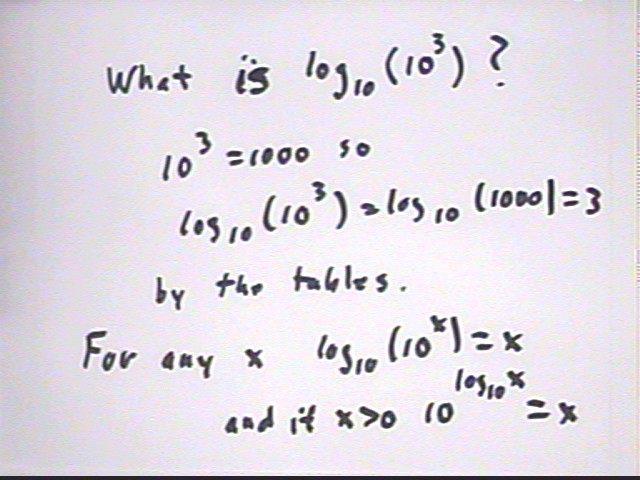
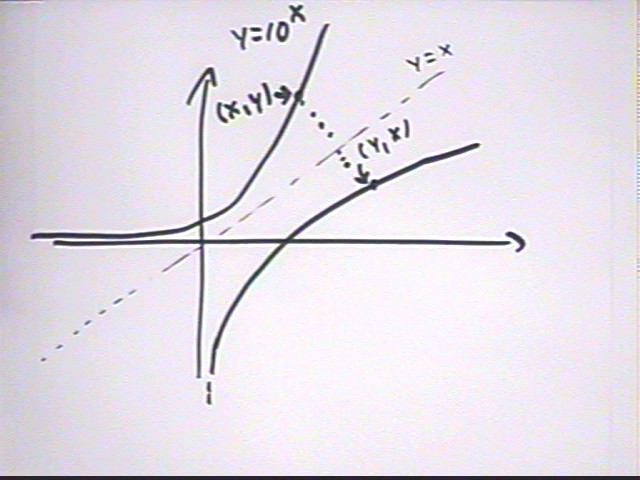
The graph of y = log{base 10} (x) is obtained by reversing the coordinates of the graph of y = 10^x. This results in a graph that is the 'reflection' through the y = x line of the y = 10^x graph.
The natural logarithm function ln(x) is defined as the inverse of the function y = e^x, in a manner completely analogous to the definition of the base-10 log:
