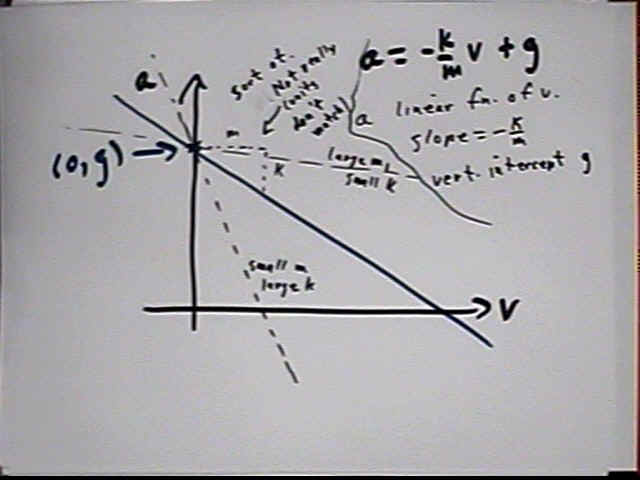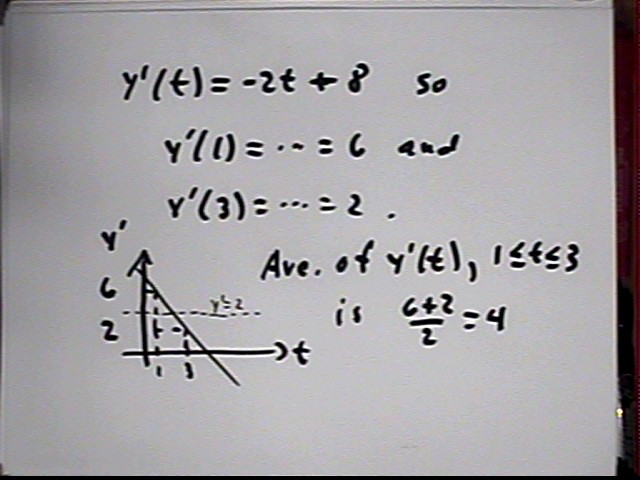
Calculus
I Quiz 0904
If the rate at which depth changes is given by y ' (t) = - 2 t + 8 then what are the rates of depth change at t = 1 and t = 3?
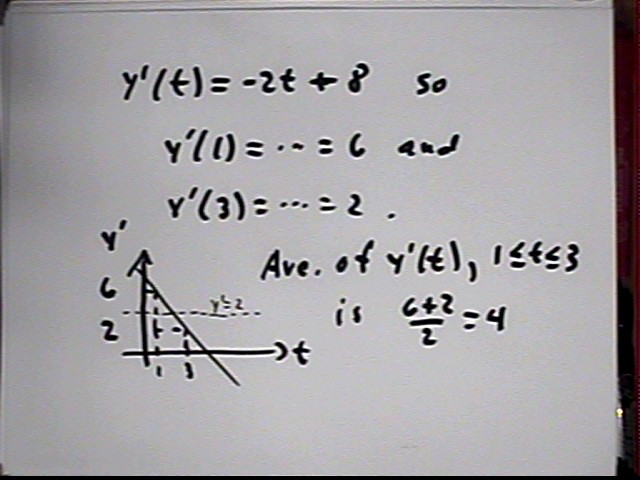
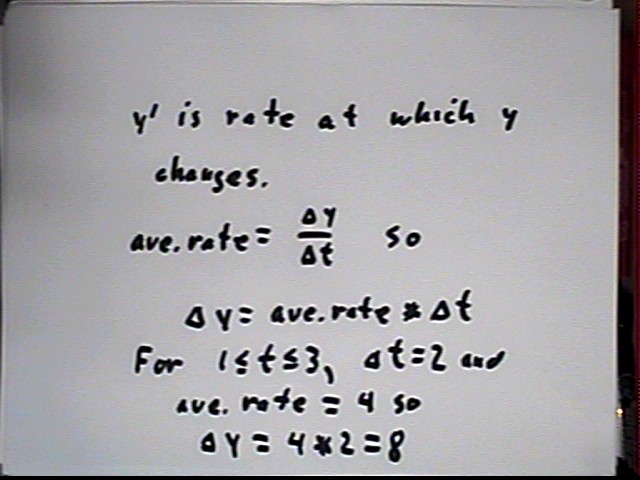
For the given rate-of-depth-change function y ' (t) what is the depth function y(t)?

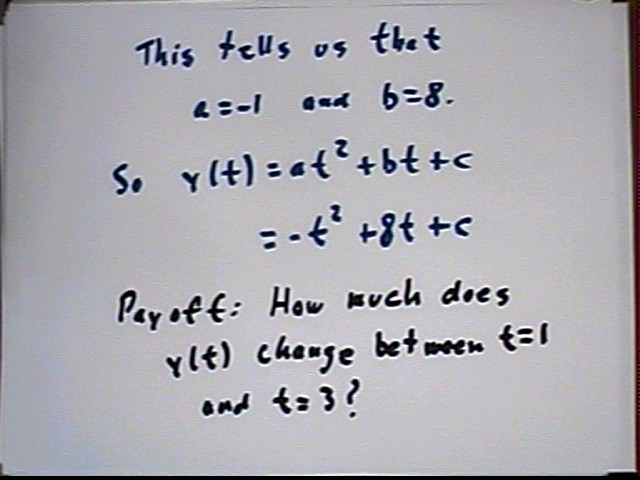
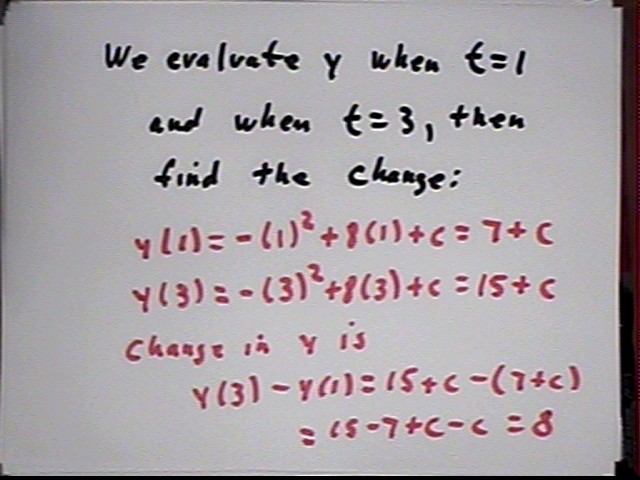
The rate function y'(t) can be derived from the amount function y(t) by simplifying the expression for [ y(t+`dt) - y(t) ] / `dt, then letting `dt shrink toward zero. This process is known as differentiation, and we'll develop rules for differentiating functions as we go through the course.
The change-in-amount function y(t) can be found by reversing the process, using the formula for y ' (t) and the relationship between the y(t) and y'(t) formulas, to get a specific function y(t). This function will contain an unspecified parameter, usually called c, which disappears when we subtract the values of y(t) at two t values in order to find the change in y. The process of constructing y(t) from y ' (t) is called integration.
For a linear y ' function we get a quadratic y function. Estimating change in y using average value of y ' over a t interval yields the same result as integrating the y ' function to get a change-in-amount function y, which is evaluated at two t values (endpoints of the t interval) to determine change in y.

Problem 35 from the text:
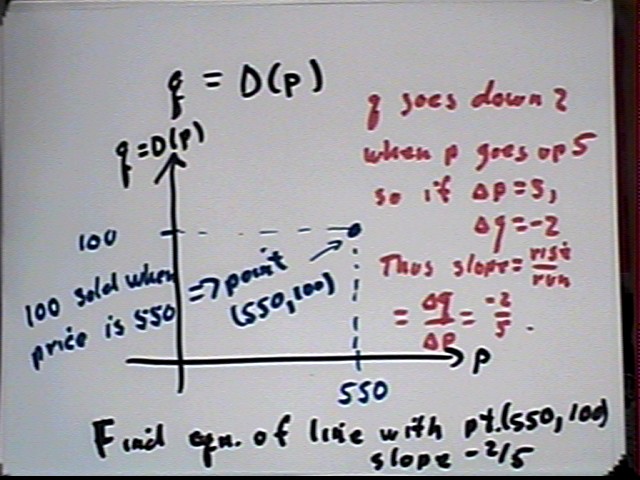
Problem 38 from the text: