What is the expression for the change in your y(t) = .1 t^2 - 5 t + c function between clock time t and clock time t + `dt?
Note that `d means the Greek capital Delta (the triangle thing).
Value of y at t is y(t) = .1 t^2 - 5 t + c
Value of y at t + `dt is
y(t + `dt) = .1 (t + `dt)^2 - 5 (t + `dt) + c
We expand this then simplify to get
.1 ( t^2 + 2 t `dt + `dt^2) - 5 t - 5 `dt + c
= .1 t^2 + .2 t `dt + .1 `dt^2 - 5 t - 5 `dt
The change in y is
`dy = y(t + `dt) - y(t) =
[ .1 t^2 + .2 t `dt + .1 `dt^2 - 5 t - 5 `dt ] - [ .1 t^2 - 5 t + c ] =
.2 t `dt + .1 `dt^2 - 5 `dt
What is the expression for the average rate at which your y(t) function changes between clock time t and clock time t + `dt?
The average rate of change is `dy / `dt = [ .2 t `dt + .1 `dt^2 - 5 `dt ] / `dt = .2 t - 5 + .1 `dt.
Homework: What is the average rate of change of y = a t^2 + b t + c between clock times t and t + `dt? What happens to this expression as `dt shrinks toward zero?
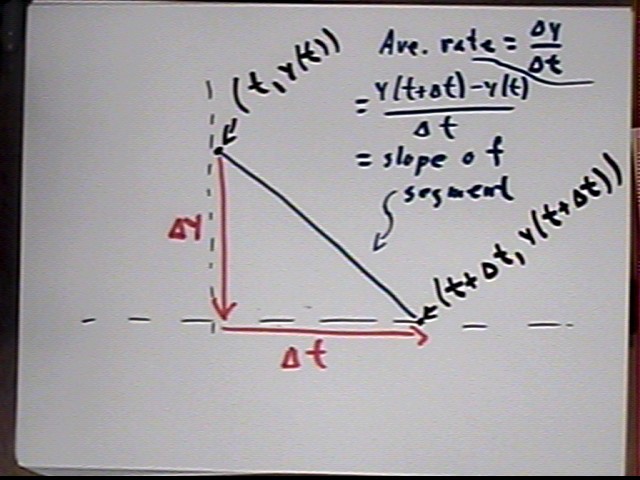
The average rate of change of y with respect to t is
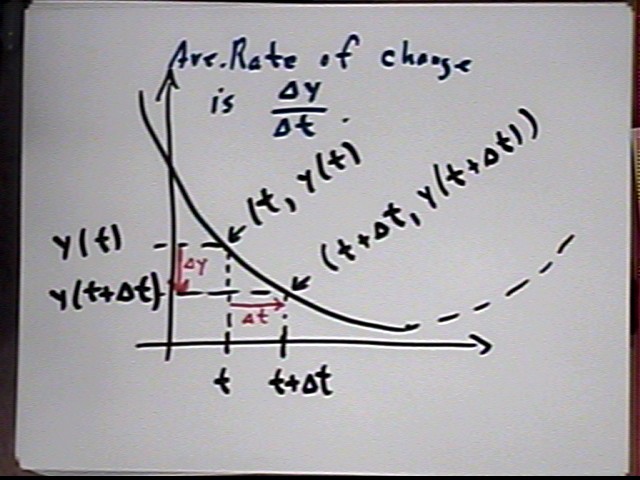
This is depicted by the graph in the figure below:

An enlarged picture:
We obtain expressions for y(t) and y(t+`dt):
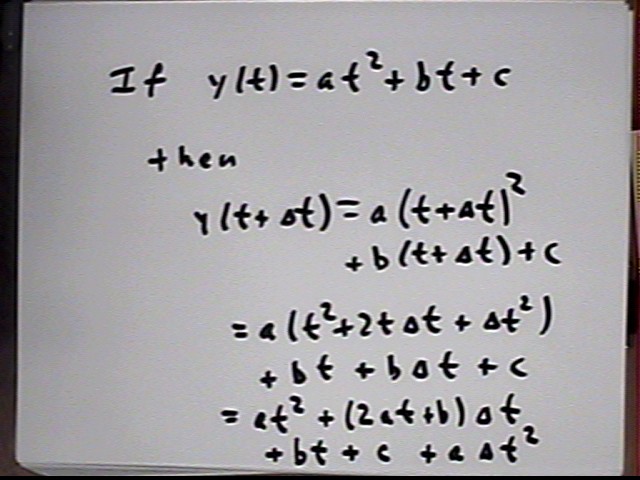
We now calculate the change `dy in y:
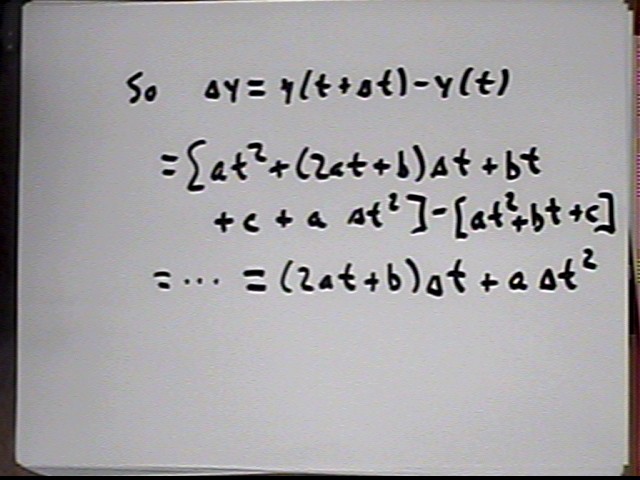
Now we can get the expression for `dy / `dt:
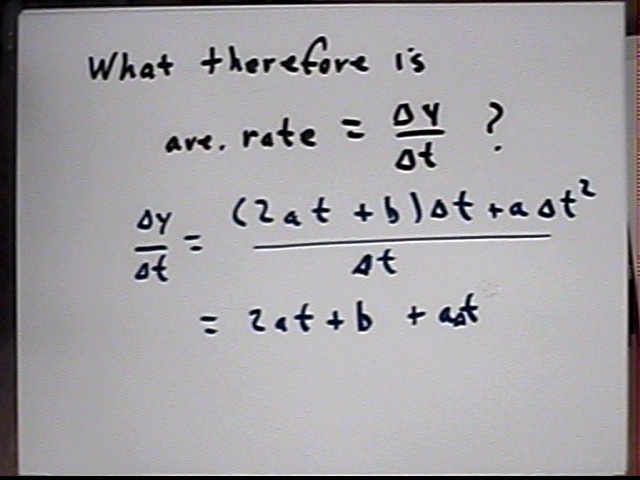
That last line reads 2 a t + b + a `dt.
We therefore see that `dy / `dt = ... = 2 a t + b + a `dt.
What can we say about the value of this expression if `dt is very, very tiny (as tiny as you want)?
If `dt is tiny enough then a `dt is also very tiny.
This means the `dy / `dt = 2 a t + b + a `dt is very close to 2 a t + b.
In the figure below we show the segments whose slopes represent `dy / `dt for smaller and smaller values of `dt. This is an important picture.
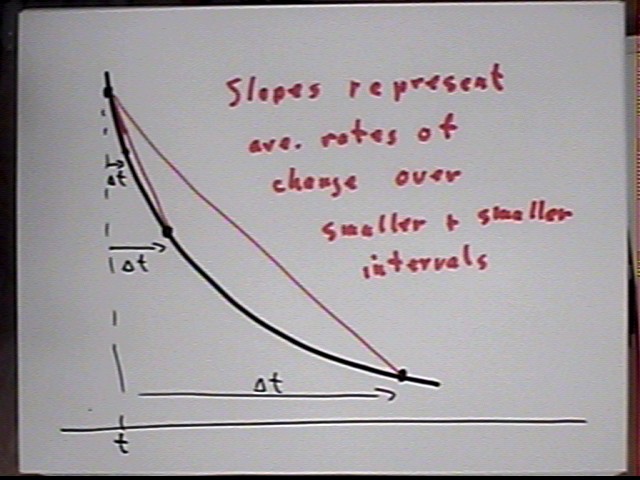
On a graph of y vs. t, what does `dy / `dt represent?
This represents the average slope between the t and t + `dt points on the graph, which is interpreted as the average rate of change of y with respect to t over the interval.
As `dt gets tinier and tinier what does `dy / `dt represent?
`dy / `dt will represent ave slopes over tinier and tinier intervals `dt, which is interpreted as ave rate of change over tinier and tinier time intervals.
Calculus
I Quiz
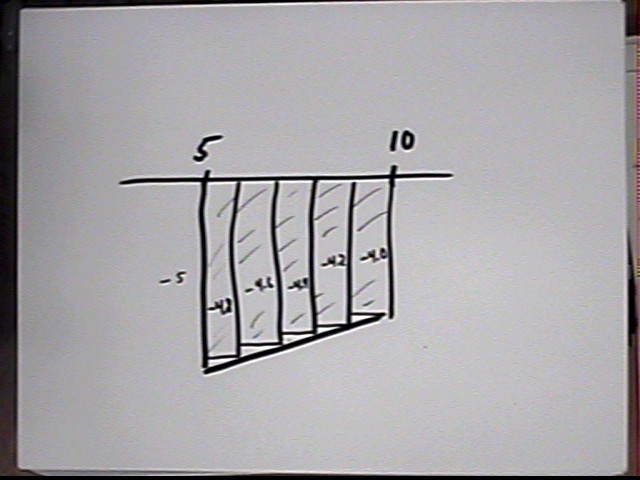
If
water depth is changing at rate y ‘ = -5 cm/sec when t = 5 seconds, and at
rate y ‘ = -4 cm/t at t = 10 seconds, then how much change in depth would you
expect between these two clock times?
Rate of depth change goes from -5 cm/s to -4 cm/s. Think about what this means. The water surface is moving downward at -5 cm/s when t = 5 sec and at -4 cm/s when t = 10 sec. Move your finger across a ruler at 5 cm/s (it takes 1 sec to move 5 cm) and imagine the water surface doing the same.
y ' is the velocity v of the water surface. The graph below shows how v changes between t = 5 sec and t = 10 sec, and why the average rate of change of velocity is -4.5 cm/s:
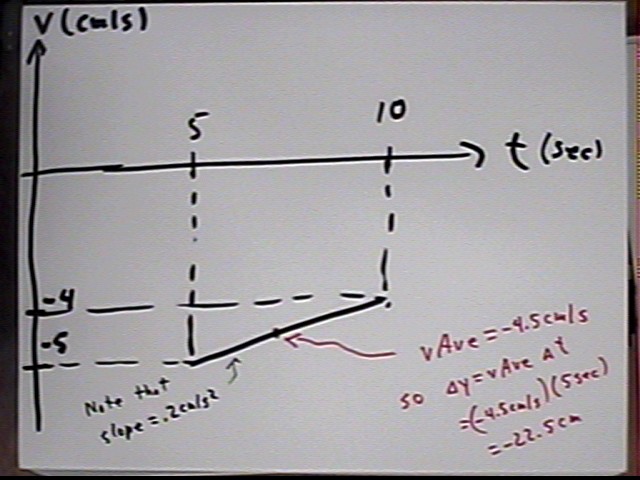
The change in depth is `dy = vAve * `dt = ... = -22.5 cm.
(see also footnote 2)
When
y(t) = a t^2 + b t + c then the rate at which y changes with respect to t is
given by the function y ‘ (t) = 2 a t + b.
If
y ‘ is given by the function y ‘ (t) = .04 t – 6 then what can you say
about the depth function y(t)?
(see also footnote 1)
We solve this by identifying a and b from the given information that y ' (t) = a t + b and that y ' (t) = .04 t - 6.
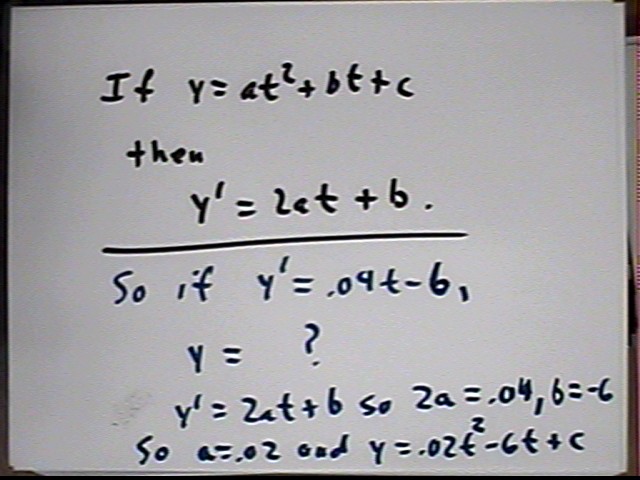
If
y ‘ (t) = .08 t – b, where b is the number of letters in your last name,
then what are the values of y ‘ (10) and y ‘ (30)?
By how much does y therefore change between t = 10 and t = 30?
What
is the average rate of change of the function y(t) = t^3 between clock time t
and clock time t + `dt?
Write
a proportionality formula expressing the following statement:
The rate y ‘ at which water flows from a uniform cylinder through a
uniform hole is proportional to the square root of the depth y of the water
relative to the hole.
At
what clock time will the rate y ‘ of change of the function y(t) = .02 t^2 –
12 t + 90 be 0?
What
is the range of the function y(t) = .02 t^2 – 12 t + 90?
Challenging
question:
If
y(t) = .02 t^2 – 12 t + 90 then find the rate y ‘ at which water depth
changes when the depth y is 60 cm, and also when the depth y is 30 cm.
Show that at these depths, at least, the rate y ‘ does indeed appear to
be proportional to the depth.
Really
challenging question:
See
if you can figure out a way to prove that the result of the preceding problem
holds no matter what depth in the range of the given function is chosen.
Footnotes
1. Using the fact that if y = a t^2 + b t + c we have y ' = 2 a t + b to find y ' for the given function, we identify a, b and c:
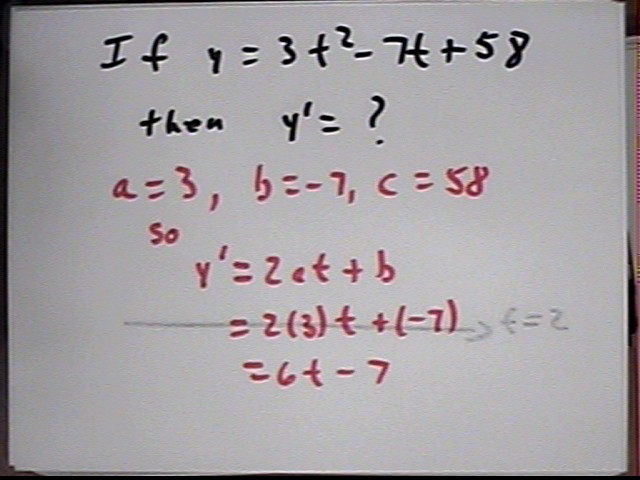
2. Suggested in class: Note that the rate increases by 1 cm/s in 5 sec, so that there is a change of .2 cm/s every second. Then rates after 1, 2, 3, 4, 5 sec are -4.8, -4.6, -4.4, -4.2 and -4.0 cm/s. So the water will move -4.8 cm, -4.6 cm, -4.4 cm, -4.2 cm and -4.0 cm during the first 5 sec, for total -22 cm.
Good suggestion but during the first second, for example, the rate isn't always -4.8 cm/s. It goes from -5 cm/s to -4.8 cm/s, so the average rate is -4.9 cm/s and the water moves -4.9 cm, not -4.8 cm. Similar comments apply to the other 1-second intervals.
A picture of the suggested method shows how the assumption of a 'level velocity' on each interval equal to the final velocity on that interval leaves off a little bit of the graph. This will be an important idea later on.