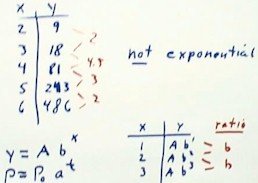
Given a table of y vs. x data in which the x values are evenly spaced, in order to determine whether the set is exponential or not we need only look at the ratios of successive y values. If the ratio is constant, then the data indicates an exponential function. We see why this is so by looking at the form y = A b^x of an exponential function.
Given a proportionality y = k x^2 and values of y and x, we determine k. From the resulting y = k x^2 relationship we can determine y for any given x or x from any given y.
When an object cools in a constant-temperature room, the rate at which its temperature changes is proportional to the difference T -Troom between its temperature T and that of the room: rate = k (T - Troom). From a given rate and a given temperature we can evaluate k. The rate of temperature change is denoted dT / dt, so we have the proportionality dT / dt = k (T -Troom). This sort of equation, in which a derivative is treated as a variable, is called a differential equation.
Given a table of y vs. x data in which the x values are evenly spaced, in order to determine whether the set is exponential or not we need only look at the ratios of successive y values. If the ratio is constant, then the data indicates an exponential function.
The data set below does not show exponential behavior, since the ratios are 18 / 9 = 2, 81 / 18 = 4.3, 243/81 = 3, and 486/243 = 2. If these ratios had come out the same, exponential behavior would have been indicated.
To see why this behavior occurs, we look at two common form of the exponential function, y = A b ^ x and P = P0 a ^ t. If we make table for the values of y = A b ^ x, using x values 1, 2, 3, we obtain corresponding y values A b ^ 1, A b ^ 2 and A b ^ 3. The ratios of successive y values are thus A b ^ 2 / ( A b ^ 1) = b^2 / b^1 = b and A b ^ 3 / ( A b ^ 2) = b^3 / b^2 = b. It is clear that this pattern will continue.
If our x values had been separated by a common x increment `dx, then successive y values would have been A b ^ x and A b ^ (x + `dx) and the ratio would have been A b ^ ( x + `dx) / (A b ^ x) = A b^x b^`dx / (A b^x) = b^`dx. If the `dx increment is always the same, then the ratio b ^ `dx will always be the same.
It should be clear that the same sort calculations could have been done based on the equivalent exponential form P = P0 a ^ t.
If the stopping distance of a car is proportional to the square of its speed, then we can write the proportionality dist = k (speed)^2. If we know that the speed of 70 mph requires a stopping distance of 177 feet, we can substitute this information into the proportionality equation and easily determine that k has the approximate value .0361 ft / mph^2. Our distance function then becomes dist(speed) = .0361 ft / mph^2 (speed)^2, where the expression dist(speed) indicates functional dependence (e.g., f(t) = ...).
This distance function is easily evaluated at 35 mph and at 140 mph to obtain distances 44.25 ft and 708 ft. Actually these calculations can be done much easier if we note that 35 and 140 are respectively the half and double of 70. Since the distance is proportional to the square of the speed, the two distances will be respectively (1/2)^2 and 2^2 times the distance at 70 mph. You should check that these multiples of 177 ft will indeed be 44.25 and 708 ft.
To see why this trick works, suppose that we have distances dist2 and dist1 corresponding to speed speed2 and speed1. Then dist2 = k (speed2 ) ^ 2 and dist1 = k (speed1) ^ 2, so the ratio of distances will be dist2 / dist1 = k (speed2) ^ 2 / [k (speed1) ^ 2]. The right-hand side can be simplified to give (speed2/speed1) ^ 2, so we have dist2 / dist1 = (speed2 / speed1) ^ 2. This tells us that we need only square the ratios of the speeds to get the ratio of the distances.
Today's class occurred on a mid-September day when the temperature reached 97 Fahrenheit. This after lows in the 40's and highs in the 60's just a few days ago.
Had we taken a large steel washer outside and allowed the midday sun to heat it, it might well have reached the temperature of, say, 160 Fahrenheit. Had we then brought back into the classroom it would have experienced a rapid decrease in its temperature. Our intuition and experienced tells us that the closer the temperature of the object is to the room temperature, the more slowly its temperature will change.
For example if we observed that the temperature of the washer fell from 160 Fahrenheit to 140 Fahrenheit during a 10-second time interval, we would conclude that on the average during the 10-second time interval the temperature T of the object was changing at the rate of -2 Fahrenheit/second. We might even predict that the rate of temperature change was very nearly -2 Fahrenheit/second when the temperature was midway between 160 Fahrenheit and 140 Fahrenheit, or 150 Fahrenheit.
By measuring temperature change over a variety of relatively short intervals we might associate a variety of rates with specific temperatures, just as we would associate the rate -2 Fahrenheit/second with the temperature 150 Fahrenheit.
The average rate at which temperature T changes with respect to clock time t is of course obtained by finding the temperature change `dT associated with a specific interval `dt of clock time. The average rate is thus `dT / `dt. This is completely analogous to the way we calculated the average rate `dy / `dt of depth change with respect to clock time for the flow model or the average rate `dy / `dx of volume change with respect to diameter for the sandpile model. If as in those examples we take the limiting value of `dT / `dt as the time interval approaches 0, we obtained and instantaneous rate dT / dt of temperature change. We thus say that the rate of temperature change is the derivative dT / dt of the temperature function T(t).
Now we expect that as the temperature approaches room temperature the rate dT / dt at which the temperature changes will decrease. For example if the rate of temperature change at temperature T = 150 Fahrenheit is indeed -2 Fahrenheit/second, then we would expect the rate at temperature T = 100 Fahrenheit to be lower. How much lower depends on the room temperature.
Assume that the room temperature is 80 Fahrenheit. Then T = 150 Fahrenheit is 70 Fahrenheit above the room temperature, whereas T = 100 Fahrenheit is only 20 Fahrenheit above room temperature. We will call these differences between washer temperature and room temperature 'temperature differences' (and we will distinguish these from `dT calculations, which might also be called temperature differences, by using the notation `dT for the differences between two washer temperatures, and referring to these differences as 'delta T's').
We see that the temperature differences, with respect to room temperature, are 70 Fahrenheit and 20 Fahrenheit for washer temperatures of 150 Fahrenheit and 100 Fahrenheit. The second temperature difference is only 2/7 that of the first. We might expect that 2/7 of the temperature difference will result in 2/7 of the rate of temperature change. In this case then, we might expect that 100 Fahrenheit the rate of temperature change would be 2/7 of the rate observed that 150 Fahrenheit, or rate(100 Fahrenheit) = 2/7 rate(150 Fahrenheit) = 2/7 (-2 Fahrenheit/second) = -.57 Fahrenheit/second.
Of course there is no good reason to expect that the rate of temperature change will be directly proportional to the temperature difference. The rate might be proportional to the square of the temperature difference, in which case we would multiply by (2/7)^2 instead of 2/7 in the above calculation. Or the rate might be proportional to the square root of the temperature difference, in which case we would multiply by `sqrt(2/7). Or the proportionality could be even more complex.
We could symbolize the process implied above. As we so before if T(t) is regarded as the temperature function of clock time, then the rate which temperature changes is dT / dt. If we symbolize room temperature as Troom, then the temperature difference at temperature T will be temperature difference = T - Troom. We would therefore be seeking the relationship between the rate dT/dt of temperature change and the temperature difference T - Troom.
If as in the above example we make the reasonable assumption that the rate of temperature changes directly proportional to the temperature difference, we would express this proportionality as
rate prop to temp diff
dT / dt = k (T - Troom).
Had we assumed that the rate is proportional to the square the temperature difference we might have written
dT / dt = k (T - Troom)^2,
and if the assumption wasn't the rate is proportional to the square root of the temperature difference we would probably have written
dT / dt = k `sqrt(T - Troom).
If we assume the direct proportionality, then if the rate is in fact -2 Fahrenheit/second when the washer temperature is 150 Fahrenheit, then we can easily evaluate k, as in the figure below.
Having obtained the value k = -.028 Fahrenheit/second/Fahrenheit, or as expressed in the figures k = -.028 degrees/second / degree, we write the proportionality as
dT / dt = -.028 ( T - 80),
for the moment suppressing the units and understanding that everything is measured in Fahrenheit degrees and seconds.
This equation relates the rate of change dT / dt to an expression involving T. Thus we have related a derivative of T to a function of T. The equation expressing such a relationship is called a differential equation. Loosely speaking, differential equations are 'rate-of-change' equations, in which rates of change, or derivatives, appear as variables in the equation.
Just as we can solve algebraic equations using the laws of algebra, we can solve many differential equations using the procedures of calculus.
For the given differential equation above, in which dT / dt is equal to a linear function of T, the solution we obtain will be the temperature function T(t). For this specific equation the solution will be an exponential function. The function is in fact T(t) = A e^(-.028 t) + c. The two parameters A and c can be fairly easily evaluated from knowledge of the room temperature (e.g., since the temperature of the object approaches the room temperature as an asymptote, and since T(t) approaches T = c as an asymptote, c must be the room temperature; A is evaluated in a way we will see later from our knowledge that dT / dt = -2 when T = 150).
Had the equation been dT / dt = -.028 (T - Troom) ^ 2, or dT / dt = -.028 `sqrt(T - Troom) we would not have obtained an exponential function as are solution. The second of these equations would in fact have given us a quadratic solution.
Before we can actually see how these solutions come about we will need to develop a good theory of derivatives and integrals.
"