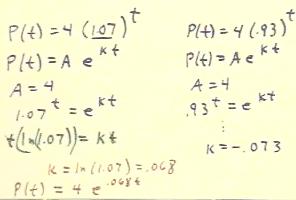
Quiz Problems
The first of the two quiz problems was to express P(t) = 4 (1.07) ^ t in the standard exponential form P(t) = A e^(kt), and to express P(t) = 4 (.93) ^ t in the same form.
As a shown in the figure below, it should be clear that the first function will be in standard form if A = 4 and e^(kt) = 1.07^t. The second of these conditions is in equation can be solve for k by taking the natural log of both sides. We obtain k = ln(1.07) = .068.
We note that the base 1.07 of the first form corresponds to a growth factor 1.07, and a growth rate of .07. The parameter k is just the natural log of the growth factor; since the growth factor is greater than 1 its natural log is greater than 1 (recall that the natural log of 1 is 0).
The second part of this problem is identical to the first except that the growth factor is corresponding to a growth rate of -.07. This time we obtain k = -.073, corresponding to the natural log of .93. The function, which is not shown in the figure, is P(t) = 4 e^(-.073 t).
In the second quiz problem we were given a rate function dy / dx = x^2, and the fact that when x = 2, we have y = 10. We were to find the rate of change at x = 2, the change in y as x increases to 2.5, and the new value of y.
When x = 2, the rate dy / dx is dy / dx = x^2 = 2^2 = 4. We might wish to think in concrete terms, regarding x as clock time in seconds and y as a depth function with depth expressed in cm. Then the rate would be 4 cm / sec.
If we regard x as clock time then the increase of tax from 2 to 2.5 corresponds to a time interval of .5 seconds. The 4 cm / sec rate over the period of .5 seconds would then imply the approximate `dy = dy/dx * `dx = 4 * .5 = 2, corresponding to 2 cm.
In any case if y starts out at 10 and increases by 2,the new value of y will be 12.
We can express the above calculations in table form, as in the figure below. From the given conditions we see that the first values of x and y must be 2 and 10. We see that dy / dx must be 4 when x = 2, and that an x interval `dx of .5 will therefore imply a change in y of approximately `dy = dy/dx * `dy = 4 * .5 = 2. The time interval `dx and the change `dy in y will result in x values of 2.5 and 12 respectively, has expressed in the second row of numbers.
The process is continued in the second row, with dy / dx = x^2 = 2.5^2 = 6.25. With the `dx of .5, we find the approximate `dy to be (6.25) * .5 = 3.1. These values of `dx and `dy imply new x and y values of 3.0 and 15.1. The process can continue indefinitely.
Predictor-Corrector Method
The homework problem given in class last time was to continue the process imply by the differential equation dT / dt = -.028 (T - 80), corresponding to the cooling of a certain object in an 80-degree room, if it is known that the temperature of the object it clock time t = 0 is 150 degrees. The first row indicates that the 150 degree temperature implies a rate of temperature change of -2 degrees/second, which for time interval `dt = 5 sec. yields of temperature change of -10 degrees. Thus the temperature clock time t = 5 seconds is approximately T = 140.
The calculation to this point overestimates the rapidity of the temperature change, using the change corresponding to T = 150 for the entire five second interval. In fact as the temperature decreases the rated which the temperature changes will also decrease, resulting in less temperature change than predicted.
The second set of calculations below (in green) indicates the prediction of the clock time t = 5 second temperature, starting from the same conditions but using a time interval of dt = 1 second instead of five seconds. This requires five sets calculations, and results in a clock time t = 5 temperature of 140.8 degrees, rather than 140 degrees. Since we expect rate deviations over one second time intervals to be much less than the rate deviations over a five second interval, and since the calculation as expected yields a somewhat higher temperature then that obtain with the five second interval, this result is very plausible.
We returned out to the first set of calculations, noting that the T = 140 degree temperature implies a rate of -1.68 degrees/second. This predicted temperature, and hence this rate, are pretty close to the actual temperature and rate at the end of the five-second interval. It makes the certain amount of sense to average the rate at the beginning of the interval with the rate at the end of the interval. Doing so we obtain a 'corrected' average rate of -1.84 degrees/second. Over a five second interval this rate implies that change of (-1.84 deg / sec) * 5 sec = -9.2 deg, and hence a temperature of 140.8 at clock time t = 5 seconds. This agrees very well with the T = 140.8 (actually a rounded value and not exactly equal to the 140.8 just obtained) that resulted from the `dt = 1 second interval.
We call this a 'predictor-corrector' method, which we use the rate at the beginning of the interval to predict the value of the independent variable at the end of the interval, use this value to predict the rate at the end of the interval, and average the initial and final rates for the interval to obtain an approximate average rate. This average rate is then applied over the interval.
This method is summarized in the table below. We begin as usual with t = 0 and T = 150, calculating dT / dt from the differential equation, using this rate with the time interval 5 to determine the predicted change in temperature and hence the predicted t = 5 temperature of 140 deg. We then determine the predicted rate at this temperature. These last three calculations give us predictors, which will be discarded when we are done with them.
The predicted end-of-the-interval rate is then average with the beginning-of-the-interval rate to get the 'corrected' rate, which is applied to get the 'corrected' `dT. This corrected temperature changes then used to find the approximate temperature at the new clock time, in this case 140.8 degrees at clock time t = 5 seconds.
As a rule of thumb, we can generally obtain comparable accuracy with the predictor-corrector method when using a time increment `dt which is about 10 times as great as with the original method. This means that we can perform 1/10th the number of steps with a predictor-corrector method; though each step is slightly longer than with the original method, we still get by with a great deal less work.
The Sine and Cosine Functions
We begin by defining the radian, the unit of which we measure angles in calculus. One reason we use the radian to measure angles is that the derivative of the function y = sin(t) is dy/dt = cos(t), provided that we measure are angles in radians. If the angle is measured in degrees, the derivative is dy / dt = `pi/180 cos(t), which is far less convenient. Another is that it is much easier to relate arc lengths to angles when the angles are measured in radians.
The figure below shows a definition of the radian. We begin with a circle with some radius r at a set of x-y coordinate axes centered at the center of the circle. A radian is the angle for which the arc length along the circle is equal to the radius of the circle. The sector formed by this angle can be thought of as an equilateral triangle on which one side has been beaten out into an arc of a circle, the process which reduces the angle formed by the two remaining straight lines slightly below its original 60 degrees (a radiant is approximately 57 degrees).
It should be clear that since an angle of 1 radian corresponds to an arc length `ds = r, and angle of 1/2 radians should correspond to an arc length of `ds = 1/2 r, and an angle of 2 radians should correspond to an arc of `ds = 2 r. These observations are summarized in the short table below. We note that the arc length `ds seems always to be the product of `dtheta and r, and it should be obvious that this pattern will continue for any angle `dtheta. If we have a sector of the circle with radius r, as shown below, with an angle `dtheta, then the arc length would be `ds = `dtheta * r, or `ds = r `dtheta.
Since the circumference of the circle is 2 `pi times the radius, we can fit 2 `pi arcs each of length `ds = r around the circle. It follows immediately that we can get 2 `pi radians of angular measure around the circle, since each arc of length r corresponds to an angular measure of one radian. It follows that 360 degrees of angular measure is the same as 2`pi radians of angular measure. We could write 360 deg = 2 `pi rad and solve for either degrees (` deg = 2`pi / 360 rad = `pi / 180 rad) or radians (1 radian = 360 deg / 2 `pi = 180 / `pi deg).
We now observe that any point on a unit circle (i.e., a circle of radius 1), where the origin of x-y coordinate system coincides with center the circle, has a coordinate representation (x, y). The first coordinate x can be thought of as the position on the x axis of a point projected straight downward from the point on the circle. It can also be thought of asthma displacement from the origin to that point, represented by a red arrow labeled 'x'. The y coordinate can be similarly seen in terms of a projection running horizontally from the point (x, y). We note that the projection lines (the dotted red lines) make right angles with the coordinate axes, and hence we have formed two right triangles, each with the radio line from the origin to (x, y) as its hypotenuse.
The triangle formed with one of the shorter sides along the x axis is depicted below. We note that its 'vertical' side is y and that its hypotenuse is equal to the radius of the circle, which is 1. By the Pythagorean Theorem it follows that x^2 + y^2 = 1.
The definition of the sine and cosine functions can be expressed very simply: for this situation, a point on a unit circle who center coincides with the origin of the set of coordinate axes as depicted here, the angle `theta as measured from the x axis to the radial line running from the origin to (x, y) has sine and cosine values
sin(`theta) = y and cos(`theta) = x.
We can re-sketch the (green) triangle, replacing x and y with the cosine and the sign of `theta, respectively. We note that the Pythagorean Theorem tells us that sin^2(`theta) + cos^2(`theta) = 1.
We can sketch a graph of the sine function by imagining three bugs. The first bug crawls at a constant speed around the circle. The second moves at a constant speed along the horizontal axis of the graph located horizontally opposite the circle. The third bug keeps its segmented eyes on the other two and space directly across from the bug on the circle and directly above the bug on the axis. Its path is indicated by the red curve, which has the shape of the familiar sine curve.
The horizontal axis of the graph is labeled `theta, and the vertical axis could be labeled y. When the first bug has completed its circle, having crawled through an angle of 2 `pi rad, the position of the second bug will correspond to an angle of 2 `pi rad. We labeled this position on the horizontal axis 2 `pi. Halfway to this position, corresponding to the instant when the first bug crosses the negative x axis, the angle should be half of 2`pi, or `pi (note that if an angle is given without units, it is automatically understood to be in radians). Halfway to this position, corresponding to the instant at which the first bug reaches the 'highest' point on the circle, the angle is `pi / 2. This angle could be divided into three parts, each 1/3 of `pi/2, or `pi/6, greater than the last.
The angle `pi / 6 corresponds to 1/12 of the complete circle. In degrees this angle is 30 degrees. The circle in the lower left of the figure below is labeled with multiples of this angle. These multiples are `pi/6, 2 `pi/6, 3 `pi/6, ..., 12 `pi / 6. Some of these angles of course will be expressed differently in lowest terms (e.g., 2 `pi / 6 = `pi / 3, 4 `pi / 6 = 2 `pi / 3, etc.). You should be able to reproduce this figure instantly anytime you need it.
The circle at lower right indicates that multiples of `pi / 4 can be expressed similarly. `pi / 4 corresponds to 1/8 of the circle, or 45 deg. You should also be able to reproduce this figure instantly anytime you require it.
The figure below shows two graphs, the 'red' graph corresponding to a bug which completes the circle in 12 seconds and the 'purple' graph that a bug which completes the circle in 4 seconds. The horizontal axis is now labeled with clock time t, and the point corresponding to 12 seconds is labeled in red (it is a little hard to see the '1' in the '12').
The bug corresponding to the red graph will complete its circle in 12 seconds, with its angular position on the circle starting at `theta = 0 and ending at `theta = 2 `pi. Thus as clock time t goes from 0 to 12 seconds, the angular position of the bug goes from 0 to 2 `pi. You should convince yourself that the expression `theta = 2 `pi / 12 * t has this property; if you plug 0 in for t you get `theta = 0, as we wish, and if you plug in 12 for t you get `theta = 2 `pi, again as required. The corresponding graph is therefore of the function y = sin(`theta) = sin(2 `pi / 12 * t) = sin(`pi/6 * t).
Similarly if a bug completes the circle in 4 seconds, is angular position will be `theta = 2 `pi / 4 * t. The graph of the function will therefore be the graph of y = sin(`theta) = sin(2 `pi / 4 * t) = sin(`pi / 2 * t). We can generalize this: If we know the period required for the bug to crawl away around the circle, then if its angular position clock time t = 0 is `theta = 0, then its angular position is given by `theta = 2 `pi / period.
We can generalize this: If we know the period required for the bug to crawl away around the circle, then if its angular position clock time t = 0 is `theta = 0, then its angular position is given by `theta = 2 `pi / period.
If we wish to find the period of a function such as y = sin(7t), we simply note that `theta = 2 `pi / period and `theta = 7 t, so 7 t = 2 `pi / period. We easily solve for the period, which is found to be 2 `pi / 7.
"