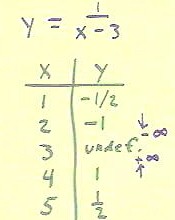
We begin by considering the function y = 1 / (x-3). In order to graph this function we might begin by exploring its behavior by means of the table. However, if we don't choose our x values intelligently we won't get a good picture of the important behavior of the graph.
If we look at the function y = 1 / (x-3) we see that its denominator will be zero when x = 3, so perhaps its most interesting behavior will occur near x = 3. We therefore begin by making the table of x values centered at x = 3.
We quickly see that as we move away from x = 3 in the negative direction, we obtain negative results whose magnitudes decrease in a predictable pattern (-1, -1/2, then obviously from the function we will have -1.3, -1.4, ...). Moving away from x = 3 in the positive direction, we obtain positive results whose values change in a similar pattern. We therefore conclude rather quickly that as x becomes large in the negative direction our y values will approach zero through negative values, and that as x becomes large in the positive direction our y values will approach zero through positive values.
We of course note that when x = 3, we have division by zero, which is undefined. If we imagine x changing from 2 to 3, we see that the denominator x - 3 becomes smaller and smaller, while still remaining negative. The resulting value of 1 / (x-3) will therefore be increasingly large negative numbers, and our y values will therefore approach -infinity.
Similarly when x goes from 4 to 3, x - 3 approach is zero through positive values. As a result, y = 1 / (x-3) will become larger and larger, always remaining positive, and our y values will therefore approach +infinity.
The resulting graph is shown below, with its vertical asymptote at x = 3 and horizontal asymptote at the x axis.
We next consider the function y = (x ^ 2 - 2 x - 3) / (x + 3). We begin by looking for those x values which make either the numerator or the denominator zero. By setting the numerator equal to zero we see that the resulting quadratic equation has solutions x = 3 and -1. We note that when the numerator is zero, as long as the denominator is not zero the fraction will have value zero.
Clearly the denominator zero at x = -3. Since the numerator is not zero at this value, we see that as x approaches -3, y will approach either + infinity or -infinity, as in the preceding example.
We also look at what happens when x is either a large positive or a large negative number. In either case, y will be approximately equal to x^2 / x when x is large enough that the -2x - 3 becomes irrelevant to the numerator and the 3 irrelevant to the denominator. Since x^2 / x is positive for positive values of x and negative for negative values, we see the large-x behavior summarized in the figure below.
The resulting graph is depicted below. The zeros at -1 and 3 our indicated on the x axis. We also indicate the y-intercept, obtained by letting x = 0 (clearly we obtain y = -1).
At the asymptote x = -3, we note that as we approach the asymptote from the right, with x values > -3, both numerator and denominator are positive so that the quotient will be positive, and y will approach +infinity. If we approach the asymptote from the left, with x values < -3, the denominator will be negative while the numerator will remain positive and y will hence approach -infinity.
For large positive values of x we see the graph moving off toward large positive values of y. We have not shown how large negative values of x give us large negative values of y. You should consider this question and attempt to draw a reasonable graph depicting this behavior. Note that y cannot be zero for any value of x other than those depicted.
(Note of interest: if we do a long division of the numerator by the denominator we obtain the quotient y = x - 5 + 12/(x+3). For values of x near -3 the 12 / (x+3) term is significant. For large positive or negative values of x this term is very nearly zero and therefore insignificant. For large positive and negative values of x, we therefore see that y will be approximately x -5, and that the graph of our function will therefore lie near the graph of x -54 large positive and negative x values. You don't have to know this at this point, but it is pretty interesting).
We next consider a text problem. A cylinder has a constant volume. The question concerns what happens to its surface area if its radius approaches zero.
We begin by considering the effect of cutting the radius in half. If we think of the cylinder is composed of tiny cubes, then cutting the radius in half will decrease the width and length of each cube but not its height. Decreasing the width will tend to decrease the volume of the cube to 1/2 its original volume, and decreasing the length will tend to decrease this volume to 1/2 its former value, resulting in a cube with 1/4 of its original volume. The height must therefore be increased by factor of 4 to compensate. Therefore when we decrease the radius to half its value we must increase the altitude of the cube to 4 times its value.
We can also see this by considering the formula V = `pi r^2 h for the volume of a cylinder. If we decrease r to r/2, then it will be necessary to increase the altitude to 4h, so that the resulting volume `pi (r/2)^2 (4h) will be the same as the previous volume (note that (r/2)^2 * 4h = (r^2 / 4) * 4h = r^2). Similarly if r decreases to r/k, h must increase to k^2 h in order to maintain the same volume.
If we look at the formulas for volume and surface area of a cylinder, we see that the surface area expression involves both r and h as variables. We want only r as a variable so we can gauge its effect on the surface area. If we solve the formula for the volume of the cylinder for the altitude h, we can substitute the resulting expression for h in the formula for the surface area and thereby eliminate h. Noting that the volume is a constant, we see that this solution will not introduce another variable into the surface area formula.
The resulting surface area formula is S = 2 V / r + 2 `pi r^2. As r -> 0, the second term also approaches zero. However the first term will clearly approach infinity. So have the somewhat surprising result that the surface area of the cylinder will become infinite if it's volume remains constant and its radius shrinks to zero.
The idea of continuity is illustrated by the graphs in the figure below. The first graph represents a situation in which a large and bad-tempered individual has drawn a line on the pavement and told you not to cross it. As you approach the line you feel no pain. Assuming that the individual is attentive to the promise made, you'll instantly begin feeling significant pain upon crossing the line.
The graph is not proceed continuously from the state of no pain to the state of significant pain. It jumps suddenly. We therefore say that the graph is not continuous at the position of the no-cross line.
The second figure depicts a graph with a vertical asymptote, perhaps the function y = 1 / (x-3) considered earlier. The graph is not even defined at x = 3. We therefore say that the graph is not continuous at this point. It is perfectly continuous up to this point, and again after passing this point, but not at this point.
The two functions in the accompanying graph also illustrate the idea of continuity. The first function involves trigonometric functions on the interval from -`pi / 4 to `pi / 4. On this interval we note that the cosine function, which is defined as the x coordinate of the unit circle point corresponding to the angle of which are taking the cosine, is never 0 on this interval. However the sine function, which is 0 at the angle 0, is 0 in the middle of this interval.
Since the cosine is never zero on the given interval, the fraction never has 0 has its denominator. Since the exponential function is quite smooth and continuous for all numbers, and since the sine function changes continuously over this interval, the numerator will also be continuous and the function is continuous on the given interval.
The function y = 1 / sin(`theta) is not continuous on the interval from - `pi / 2 to `pi / 2, since the value of the sine is 0 right this interval. The value the function is therefore undefined at this point in the function cannot be continuous across this point.
The text gives an example of the continuity of the function f(x) = sin(x) / x at x = 0, if we define f(0) to be 1. This example is justified in the text by a graph of f(x) vs. x. The graph below amplifies this idea.
In this figure we graph y = x and y = sin(x). An accurate graph will show that these two functions are practically identical for small values of x. It follows then that for small x values, sin(x) / x should be very nearly 1. If the graph is correct then, we conclude that the limit of sin(x) / x as x -> 0 must be 1.
http://youtu.be/wUoXt3TDvzM
In the text assignment, sections 2.1 -- 2.2, you will find that you have encountered all the ideas presented, or virtually all of the ideas presented, in the context of the depth vs. time model and in other exercises. There are slight differences in notation. For example, or we have formerly used functions like y(t) and quantities like the average rate `dy / `dt = (y(t + `dt) - y(t)) / `dt, the text might use a function f(x) and in average rate that look something like (f(a+h) - f(a)) / h, using a instead of t and h instead of `dt. This notation is more general and makes perfect sense, just as the previous notation made perfect sense within the context of the depth function. The figure below shows the slope calculation using the notation favored by the text.
"