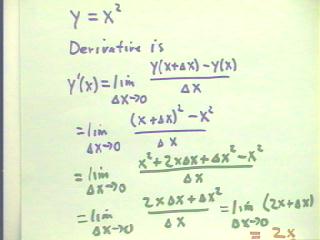
The first quiz problem was to algebraically find the derivative of the function y = x ^ 2. We therefore calculate the limit as `dx -> 0 of the difference quotient [ y(x+`dx) - y(x) ] / `dx. The calculation is very similar to, but somewhat simpler than, the calculation we did earlier with the quadratics function y = a t^2 + b t + c. The result is, of course, y' = 2x.
The second quiz question was to calculate algebraically the derivative of y = 1 / x^2. Begin calculating the difference quotient, the numerator is 1 / (x + `dx) ^ 2 - 1 / x^2. This expression has the common denominator (x + `dx)^2 * x^2; multiplying the first fraction by x^2 / x^2 and the second by (x + `dx) ^ 2 / (x + `dx) ^ 2 we obtain the numerator of the third step, x^2 / ( (x + `dx)^2 * x^2) - (x + `dx) ^ 2 / ( (x + `dx^2) * x^2). It is then straightforward to add the fractions and then to expand and simplify the numerator of the resulting expression.
Once the numerator expression is simplified we have the complex fraction shown in the first step below. The numerator consists of a fraction in the denominator is `dx. This indicates division of the numerator fraction by `dx. Since division by `dx is the same is multiplication by the reciprocal of `dx, we write the expression as in the second step. It is then easy to simplify by multiplying through the numerator by 1 / `dx. We easily take the limit of the resulting expression. We easily take the limit of the resulting expression. We see that the derivative of y(x) = 1 / x^2 must therefore be y'(x) = - 2 / x^3.
We now know the derivatives of the power functions y = x^3, y = x^2 and y = x^-2. If we make a table as in the figure below we can see two patterns to the derivatives (you should try to see the pattern before reading further).
We see that every derivative is itself a power function, and that its coefficient is equal to the power of the original function. We see also that the power of the derivative function is one less than that of the original function.
Following this pattern we can easily conjecture that the derivative of arbitrary power function y = x ^ n must be n x ^ (n-1). We will next test whether this is in fact the case.
We therefore make use of the Binomial Formula (a + b) ^ n = a ^ n + n a^(n-1) b + n(n-1) / 2 * a^(n-2) b^2 + n(n-1)(n-2) / 3! * a^(n-3) b^3 + . . . + b^n. Note how the powers of a decrease with every term while the powers of b increase with every term. Note also that at the bottom of the figure above we have shown the application of the Binomial Theorem to the expression ( a + b ) ^ 4, where n = 4.
The coefficients for the Binomial Theorem can be generated by the well-known Pascal's Triangle, shown below. Every number in the interior of the triangle is the sum of the two numbers above it; every number of the boundary is simply 1. The application of these coefficients to the first few powers of (a + b) is indicated to the right of the corresponding row of the triangle.
Notice especially how the second number in each row is equal to the power n of the expression.
At the bottom of the figure we show the application of the Binomial Theorem to the expression (x + `dx) ^ n. We show only the first few terms, containing factors of `dx^0, `dx^1 and `dx^2. Subsequent terms will continue this pattern, have higher powers of `dx as factors. Since we are eventually going to divide by `dx, all these terms will contain powers of `dx, which will approach zero as `dx -> 0.
We now apply the Binomial Formula to the expression for the derivative of y = x^n. (Note that the 'lim(`dx -> 0)' was originally left out of the expressions in the first three lines of the derivation in the figure below; it has been inserted in red and is probably too small to be read in some of the lines).
We see in the third line of the figure below how the Binomial Formula has been used to expand (x + `dx) ^ n. We have written out the terms containing powers of `dx up through `dx^2; it will shortly be clear that terms with higher powers of `dx will contribute nothing to the limit.
In the fourth line we see that the x^n terms cancel out, so that every remaining term contains at least `dx. This allows us to divide each term by the `dx in the denominator, obtaining n x^(n-1) plus terms each containing some positive power of `dx. All the terms containing positive powers of `dx will disappear as `dx approaches zero, leaving us with just the term n x^(n-1).
With a see that the derivative of y(x) = x ^ n must be n x^(n-1).
The figure below shows the graph of function y = f(x), with four points indicated. The four points correspond approximately to x values x = 1, 3, 5 and 6. We are asked to place in order, from the least to the greatest, f'(1), f'(3), f'(5), f'(6), the average slope between x = 1 and x = 3, and the average slope between x = 5 and x = 6.
It should be clear that the slopes to the left of x = 4 seem to be positive, while those to the right of this point seem to be negative. It should also be clear that the slopes steadily decrease as we move from left to right, so that f'(6) < f'(5) < f'(3) < f'(1). So we need only place the two average slopes into this sequence.
Since slopes are consistently decreasing, then the average slope between any two points to the right of x = 5 will be less than the slope at x = 5, and the average slope between any two points to the left of x = 6 will be greater than the slope at x = 6. Thus the average slope between x = 5 and x = 6 will be less than that at x = 5 and greater than that at x = 6.
By a similar argument we see that, again since the slope is always decreasing, the average slope between x = 1 and x = 3 must lie between the slopes at the two points.
We therefore conclude that f'(6) < average slope between x = 5 and x = 6 < f'(5) < f'(3) < average slope between x = 1 and x = 3 < f'(3) < f'(1).
In analyzing the values of y = sin(2x) / x near x = 0, we see that for x = .01, .001, and .0001, the values are of the form 1.99 ... 987, with greater numbers of 9's for the smaller values (it seems that the number of 9's increases by a least 24 each of the x values used). This makes it entirely plausible that lim(x -> 0) (sin(2x) / x) is 2. (Note that examination of the graphs of sin(2x) and x will reveal that the former function has double the slope of the latter near x = 0, and both pass through (0,0); this also shows that the limit should be 2).
Examination of a graph of y = sin(2x) / x also shows that as x -> 0, y seems to approach the value 2.
Note that the closer we 'squeeze' x to 0, as indicated by the red dotted lines (we imagine restricting x values between the red lines as the red lines 'squeeze' closer and closer to x = 0), the closer we `squeeze' the y values on the graph to y = 2.
The text poses the question of how close we have to squeeze x to 0 in order to squeeze y to within .01 of y = 2.
Another text problem is illustrated by the figure below. We are given to graph and asked to compare the average slope between x = 1 and x = 3 with the average slope between x = 3 and x = 5; then to compare f'(2) with f'(5); and finally to compare f(2) with f(5). It is important to sketch such situations, because it is very easy to mix up such comparisons. However, if the graph is carefully draw and labeled, we find that the comparison becomes easy.
By sketching the line segments corresponding to the average slopes, we easily see that the first average slope is greater than the second. If we note that the derivative is represented by the slope of the tangent line, then sketching the tangent lines at x = 2 and x = 5 and labeling their slopes f'(2) and f'(5) shows clearly that the first slope is greater than the second. We locate the values f(2) and f(5) by projecting vertically to the graph from x = 2 and x = 5, then horizontally to the y axis. We see clearly that f(2) < f(5).
To find the equation of the tangent line to the graph of y = x ^ 3 at x = -2, we first recall that we can find the equation of a line if we know a point on the line and its slope. We can easily find for any value of x, the corresponding point on the graph of y = x^3. We can also find a slope of the tangent line from the derivative of the function.
At x = -2, the point on the graph of y = x ^ 3 is (-2, (-2) ^ 3) = (-2, -8). Since the derivative is y'(x) = 3 x^2, the derivative at x = -2 is y'(-2) = 3(-2)^3 = 12. So the equation of the tangent line will be the equation of the line through (-2, -8) with slope 12.
An arbitrary point (x, y) will lie on the line if, and only if, y - (-8) / (x - (-2) ) = 12. This is an equation for the line. It can be put into slope-intercept form by solving for y.
Note that, near x = -2, the tangent line lies close to the graph of the function and therefore gives a good approximation to the function in that region.
"