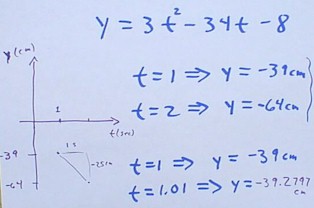
We can find the average rate of depth change between any two clock times, given a depth vs. clock time function. We evaluate the function at the two clock times to determine the depths corresponding to these clock times, then we calculate the change in depth and the difference in the clock times `dy / `dt. We use these differences to calculate the average rate. For a specific quadratic function we can symbolically calculate the average rate between clock times t and t + `dt; imagining that `dt approaches zero we obtain the actual rate-above-change function dy / dt, or y'(t).
We can generalize the above process to the general quadratic function y = a t^2 + b t + c, obtaining the general rate-of-change function y'(t) = dy / dt = ` a t + b.
From the rate function y'(t) of an unknown quadratic function we can determine the constants a and b for the function y(t) = a t^2 + b t + c. Using this knowledge we easily find the difference in the depths between two given clock times. The only thing we cannot find from the rate function is the constant c, which we need to determine the actual depth at a given time. However, without c we can still find the depth change between two given clock times.
Click on the specific video links for video explanations of these topics.
We calculate the average rate of depth change of the depth function y = 3 t^2 - 34 t - 8, between clock times t = 1 and 2, and between clock times t = 1 and 1.01.
We generalize the process, calculating the average rate of depth change for the same function, but this time between clock times t and t + `dt. We simplify the expression to get a general expression for the average rate of change.
To get the instantaneous rate at clock time t, we take the limit of the expression for the average rate between t and t + `dt, as `dt shrinks to zero.
The depth function y = 3 t^2 - 34 t - 8 yields rate of depth change y' = 6t - 24.
We now generalize to the function y = a t^2 + b t + c.
Keeping our wits about us and substituting carefully, we obtain an expression for `dy / `dt, and begin to simplify it.
Completing the process of simplification we obtain `dy / `dt = 2 a t + b + a `dt.
So we have a general formula for the rate of change function, or derivative, for any quadratic function.
Later in the course, we will find such expressions for exponential functions, power functions, trigonometric functions, and more.
We apply the knowledge we have gained to our original depth function y = .015 t^2 - 2.15 t + 88.7.
To answer the preceding question we note that the given function is a quadratic y = a t^2 + bt + c with a = .015, b = -2.15 and c = 88.7.
We didn't have to go through the whole process we used before--the whole process is contained in the formula, so all we need is the formula.
We see that knowing the depth function we can find the rate function.
Now what if we know the rate function? What can we determine about the depth function from the rate function?
The initial and final rates are easily enough found.
We see that the product of average rate and time interval is a depth change of -34.2 cm (the - signs got left off of the rates--again, shame on the lecturer, and make the correction).
There is an easier way to solve this problem of using the rate function to find the depth change between two clock times.
We can use the rate of depth change function to learn all we need to know about the depth vs. time function, and we can use such knowledge to solve this problem.
In the figure below we see that if the rate function is 2 a t + b, then the given rate function .17t - 12 implies that 2a = .17 and b = -12, so that a = .085 and b = -12.
In order to find the depth change between clock times t = 2 and t = 5, we can now simply evaluate the depth function at the two times and subtract results.
We have seen the relationship between the depth function and the rate of depth change function in two ways:
The process of computing the derivative of a function is call differentiation.
The process of turning the derivative around is called integration.
The depth vs. clock time function that we get from the rate of depth change function is called and antiderivative of the rate function.
cal01: We calculate the average rate of depth change of the depth function y = 3 t^2 - 34 t - 8, between clock times t = 1 and 2, and between clock times t = 1 and 1.01.
cal02: We generalize the process, calculating the average rate of depth change for the same function, but this time between clock times t and t + `dt. We simplify the expression to get a general expression for the average rate of change.
cal03: To get the instantaneous rate at clock time t, we take the limit of the expression for the average rate between t and t + `dt, as `dt shrinks to zero. We call this limit the derivative of the depth function with respect to time, and denote it dy/dt, or y', or y'(t), depending on what we want to express.
cal04: The depth function y = 3 t^2 - 34 t - 8 yields rate of depth change y' = 6t - 24. The rate function is the time derivative of the depth function. (note that 34 from before has accidentally been changed to 24 here)
cal05: We now generalize to the function y = a t^2 + b t + c. We will obtain a general expression for the derivative that will apply to any quadratic. We look at the graph and see that we need to find the average slope between the points (t, y(t)) and (t + `dt, y(t + `dt)). Keeping our wits about us and substituting carefully, we obtain and expression for `dy / `dt, and begin to simplify it.
cal06: We complete the algebraic details required to simplify our `dy / `dt expression, then take the limit as `dt -> 0 to obtain an expression for the instantaneous rate at clock time t. We thus have a general formula for the rate of change function, or derivative, for any quadratic function. Later in the course, we will find such expressions for exponential functions, power functions, trigonometric functions, and more. What is so neat about this?
cal07: We apply the knowledge we have gained to our original depth function y = .015 t^2 - 2.15 t + 88.7.
cal08: We see that knowing the depth function we can find the rate function. What if we know the rate function? What can we determine about the depth function from the rate function? We begin by calculating the depth change between t = 2 sec and t = 5 sec for the rate function y' = .17t - 12. We multiply rate by time interval to get depth change. But what rate do we use? The rate function keeps changing between t = 2 sec and t = 5 sec. We use the average rate.
cal09: For a linear rate function we average the initial and final rates over a time interval to get the average rate on that interval. We then multiply this average rate by the length of the interval to get the change in depth.
cal10: We apply what we know about a quadratic depth function and its linear rate function to the situation where the rate it y' = .17 t - 12 and obtain the same depth change we did when we multiplied average rate by time interval. We have in fact recovered the depth function from the rate function (except for the value of c, which depends only on the point from which we measure depth).
cal11: The process of obtaining the rate function from the depth function involves taking the derivative. When we know the rate function and recover the depth function (except for c), we go in the opposite direction. We find the antiderivative. We also call this process integration: we take the pieces of depth change we get from the rate function and put them together, or integrate them, to get the depth function.