the differential; tangent line approximation

Class Notes Calculus I

The Differential; Tangent Line Approximation

Sandpile Interpretation of the Differential

Using the idea of the differential we approximate the volume of a sandpile with volume function y = .0031 x^3 at diameter x = 30.1, given its volume at x = 30. We interpret this result in terms of the tangent line to the graph of the y vs. x function at the x = 30 point.

The Tangent Line

We use the same function as before to obtain an equation for the tangent line at the x = 30 point. We use this equation to approximate the original function in the vicinity of the x = 30 point.

Testing a Proportionality

Testing a table of velocity of a falling object vs. distance fallen to see if velocity is in fact proportional to distance fallen, we see that the proportionality v = k x gives different values of k for different (x, v) points, so that the proportionality fails. It turns out that the proportionality v = k `sqrt(x) works, as can be checked in the same way.

Sandpile Interpretation of the Differential

We use a sandpile volume vs. diameter function to illustrate what we can learn from the differential.

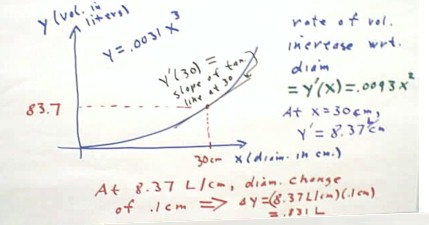
If the volume y of a sand pile, in liters, is given as a function of its diameter x, in cm, by the function

y(x) = .0031 x^3,

then the instantaneous rate at which volume changes with respect to diameter is given by the function

y'(x) = .0093 x^2,

since the derivative of y(x) = a x^3 is y'(x) = 3 a x^2.

When the diameter is 30 cm, the rate which volume changes with respect to diameter is y'(30) = .0093 (30^2) L / cm = 8.37 L / cm (so labeled, but somewhat poorly, on the figure below).

The unit L / cm indicates that the rate is measured in liters of volume per cm of diameter.

When the diameter is in the vicinity of 30 cm then, the rate of increase will be near 8.37 L / cm.

An increase in diameter of .1 cm will then result in a volume increase of

`dy = rate * `dx = 8.37 L / cm * .1 cm = .837 L.

This is only an approximation.

The actual change in volume can be found by evaluating the volume function at two values of x near 30, with the values differing by .1.

For example, we would expect y(30.1) - y(30) to be very close to .837 L, but not exactly equal to this value. The exact value would be a bit different because y ' (x), the rate at which y varies with respect to x, changes a bit between x = 30 and x = 30.1.

Or we would expect y (30.3) - y(30.2) to also be near .837 L, but probably not as close as the previous difference, since the x values are somewhat further from 30 than before.

We can see how the approximation works by looking at the graph of the function in the vicinity of x = 30.

At the y = 30 point on the graph, the instantaneous rate is given by the slope of the tangent line.
We see that the tangent line remains close to the graph for x values near 30, gradually curving away from this line as x deviates more and more from 30.

Our approximation has in fact followed the tangent line by using the rate 8.37 L / cm, as we will see below.

As we can see this is a valid approximation for small volume changes in the vicinity of x = 30. The slope of the graph doesn't change much until we get some distance away from the x = 30 point.

Video File #01

http://youtu.be/PHd71c_uJgQ

Looking closer at the graph in vicinity of the x = 30 point, we see the dotted curve representing the actual function and the solid tangent line.

The actual function hardly curves and all in this interval; the curvature has been exaggerated in order to show that there is indeed a curvature, and hence a small error in the approximation.

The slope of the tangent line is known to be 8.37 L / cm, and this slope is labeled.

If we use the tangent line rather than the actual curve to approximate the value of y at the point x = 30.1, we see that the corresponding slope triangle allows us to easily and quickly determine the change `dy resulting from a `dx of .1:

Since the slope is slope = `dy / `dx, we clearly have `dy = slope * `dx = 8.37 * .1 = .837, in agreement with our former calculation.

The Tangent Line

Video File #02

http://youtu.be/I5tFnSNkSfY

Looking again at the tangent line in the vicinity of the x = 30 point, we note that the y coordinate of the point is y = .0031 * 30^3 = 83.7.

Thus the tangent line is a straight line passing through the point (30, 83.7) and having slope 8.37.
We wish to find the equation of that straight line.

You know about the slope-intercept form of a straight line, the point-slope form and the point-point form, and probably the standard form.

The equation can be found efficiently using any of these forms.
However, we will here use a form of simple common sense that will work just fine, and doesn't require memorization of possibly meaningless formulas.

To find the equation of the line without resorting to a formula, we begin by placing a point (x,y) on the tangent line.

Then we construct the slope triangle from (30, 83.7) to (x, y).
It should be clear that the point (x, y) lies on the line if, and only if, the slope of this triangle is equal to the slope of the line.

The necessary and sufficient condition for the point (x, y) to lie on the line is therefore

`dy / `dx = 8.37.

To get the equation of the line we need only replace `dy by the value y -83.7 and `dx by the value x -30. We obtain

(y - 83.7) / (x - 30) = 8.37.

We can easily solve this equation for y, obtaining finally the slope-intercept form y = 8.37 x - 167.4.

We call this the equation of the line, meaning that whenever a pair of numbers (x, y) satisfies the equation, (x, y) must be on the line and furthermore that whenever a point (x, y) lies on the graph of the line, the ordered pair satisfies the equation.

Video File #03

http://youtu.be/BHbFdNcKl0E

We could evaluate this linear function to obtain an approximation of the cubic function y =.0031 x ^ 3.

For example, from the above result we would have obtained the approximation y(30.1) = 8.37(30.1) - 167.4 = 84.537.
This is just what we get if we add the previously determined change .837 to the x = 30 value 83.7.
This should not be a surprise, since in both places we essentially followed the tangent line to find the change in y and hence the new value of y.

We could use the tangent-line approximation function y = 8.37 x - 167.4 to get an approximate value for the function y = .0031 x^3 for any x close to 30.

The closer to 30, the better will be our approximation (look at the original graph and see how the tangent line stays close to the curve near x = 30).
We could for example approximate the volume at diameter 30.1 by plugging 30.1 into the tangent'line approximation.
We again get y = volume = 84.57, which is .837 more than the x = 30 value 83.7.

Video File #04

http://youtu.be/qA6URR0EDiQ

Testing a Proportionality

On one of the homework problems in the text, we were given velocity vs. distance data for a falling object and asked to test the hypothesis that velocity was directly proportional to distance fallen.

If the proportion is direct, then we can write v = k y.
For all (y, v) data points we should get nearly the same value of k.
We see below that it just ain't so.

In fact the data should satisfy a v = k `sqrt(y) proportionality; v is proportional to the square root of distance fallen.

You should check to satisfy yourself that this proportionality is valid, or nearly so.
To check, plug the values of y and v into the proportionality and see if k is about the same for every data point.