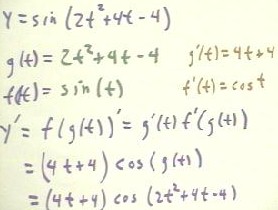
To take the derivative of y = sin(2t^2 + 4t - 4), as on the first quiz problem, first break it into a composite with the 'inner' function g(t) = 2 t^2 + 4 t - 4 and the 'outer' function f(t) = sin(t) to get y' = (4t + 4) cos(2t^2 + 4t - 4), as shown below in the usual format.
To take the derivative of y = sin(2t^2 + 4t - 4), as on the first quiz problem, first break it into a composite with the 'inner' function g(t) = 2 t^2 + 4 t - 4 and the 'outer' function f(t) = sin(t) to get y' = (4t + 4) cos(2t^2 + 4t - 4), as shown below in the usual format.
The derivative of the second quiz problem, y = cos(e^(x^2)), is a composite of three functions. the 'innermost' function is x^2; the 'middle' function is the exponential function and the 'outer' function is the cosine function. Using y for the 'outer' function and x for the 'inner' function, we can choose any 'chain' of symbols to lead from y to x. In this case we will use z for the middle function and w for the inner function, so that w(x) = x^2, z(w) = e^w and y(z) = cos(z).
The derivative will therefore be dy / dx = dy / dz * dz / dw * dw / dx, as if the dz and dw symbols cancel out (recall that they don't really cancel out that actors if they did). We therefore obtain dy / dx = -sin(z) * e^w * 2x, which is then rearranged and expressed in terms of the variable x in the last step as shown below.
To find the equation of the tangent line to the first graph at the x = .2 point, we first find accordance of that point by substituting x = .2 into the function y = sin(2t^2 + 4t - 4), obtaining y = -.0214 (approximately).
Now that we have the coordinates (.2, -.0214) of the point, we need only find the slope of the graph to find the equation of the tangent line.
The slope is found by evaluating the derivative function y'(x) at .2, as shown below. We obtain approximate slope y' = -4.8. Note that in the sketch we sketch to the tangent line before determining the slope, so that the negative slope looks positive. Please be assured that this is only an optical illusion, since your instructor would never make such an error. The persistence of this illusion, even to the eyes of the instructor, remains a mystery.
The slope is found by evaluating the derivative function y'(x) at .2, as shown below. We obtain approximate slope y' = -4.8. Note that in the sketch we sketch to the tangent line before determining the slope, so that the negative slope looks positive. Please be assured that this is only an optical illusion, since your instructor would never make such an error. The persistence of this illusion, even to the eyes of the instructor, remains a mystery.
The equation of the tangent line is found by postulating a point (x, y) on the graph and determining the conditions under which the slope from the given point to (x, y) is -4.8. The slope between the two points is, as shown by the slope triangle, (y - (-.0214)) / (x - .2), and is equal to the slope -4.8 of the tangent line, so we have the equation (y - (-.0214)) / (x - .2) = -4.8. This equation can easily be solved for y to obtain the slope-intercept form y = -4.8 x + .9386 (verify this unchecked solution).
The next example concerns of population function P(t) = 4000 e^(-.04 t) + 2000, which might for example be interpreted as a possible scenario for the human population of the Earth, in millions, t years after water and other essential resources become seriously depleted (estimates of the likelihood or unlikely that of this scenario vary widely, even when made by responsible scientists based on sound scientific evidence; it is, however, important that the opinions of responsible scientists be evaluated carefully). We wish to calculate and interpret the quantities P(40) and P'(40). Both quantities are easily calculated, as shown below (note that the derivative function was calculated using the chain rule for f(g(t))', with g(t) = -.04 t and f(t) = 4000 e^t).
P(40) represents the population 40 years after the beginning of the exponential decline. This population is 2800 million, slightly less than half the 6000 million 40 years before, at t = 0. P'(40) represents the annual rate at which population is changing 40 years after the beginning of the decline. The rate is -32 million, which represents the number by which annual deaths outnumber births.
Another example concerns the red dot projected by a laser light pen on a flat screen as the pen is held with its far end fixed at a point 13 cm from the screen and rotated about this point at a constant rate (i.e., with the angle 'theta of the pen changing at a constant rate) along the pen's axis. We wish to find a speed at which the dot is moving across the screen when the angle between the pen and a line perpendicular to the screen is `theta. This situation is shown in the figure below.
We let y stand for the position of the point on the screen, with respect to its position when `theta = 0 (i.e., when the pen is aimed directly at the screen, with the light being striking perpendicular to the screen). We first find the rate at which the position of the dot is changing with respect to the angle `theta.
We can see from a simple picture that the change `dy in the y coordinate corresponding to a uniform change `d`theta in the angle is not uniform, but increases as `theta increases toward 90 deg or `pi / 2 radians.
We find the relationship between `theta and y from the triangle shown about halfway down in the figure below. It should be clear that the ratio y / 13 is equal to the tangent of `theta. So as shown we easily determine that y = 13 cm * tan(`theta). We therefore see that dy / d`theta = d / d`theta (13 cm * tan(`theta)) = 13 cm * (1 / cos^2(`theta)).
One condition of the problem was that the angle changes at a uniform rate. This would imply that the angle would be a linear function `theta(t) = (constant1) * t + constant2, where the two constants could be any fixed numbers. We can best understand what happens in this case if we first consider consider what happens if `theta is a nonlinear function. For example, we consider below what happens if `theta(t) = .2 t^2.
As shown below, in this case y(t) becomes a composite function y(t) = 13 cm * tan(.2 t^2). The derivative of this function is the derivative of f(g(t)) with g(t) = .2 t^2 and f(t) = tan(t). The derivative is the velocity v(t) = y'(t) = 5.2 cm / (cos^2 (.2 t^2) ).
We note that the acceleration function, representing the rate at which the velocity changes, would be the second derivative a(t) = v'(t) = y''(t) of the position function y(t). We note also that the calculation of this derivative would be somewhat messy, but not difficult.
In general if `theta is a function of t, we find that y(t) = 13 cm * tan(`theta(t)), with derivative y'(t) = `theta'(t) * 13 cm / cos^2(`theta(t)). Thus, for linear `theta(t) = c1 * t + c2, for constant values c1 and c2, we have `theta'(t) = c1 and y'(t) = c1 * 13 cm / cos^2(`theta(t)).
Derivatives of Inverse Functions
We can follow a standard procedure to find the derivative of the inverse function of any function whose derivative we know. We begin with the example of finding the inverse function of g(x) = x^(1/2). We can of course find this derivative from the power function rule, the recall how uncomfortable we have told you to be about the fact that the power function rule as proven so far only applies only to integer powers, and not to fractional powers.
To actually prove that the derivative of this function is 1 / (2 x^(1/2)), we note that the inverse function of g(x) = x^(1/2) is f(x) = x^2. We very quickly conclude that the composite function f(g(x)) is just equal to x, as it must be for any pair of inverse functions. It follows that the derivative of this composite is f(g(x)) ' = 1.
We can also calculate the derivative using the chain rule, of course. Noting that g'(x) will remain unknown, since it is what we are trying to find, and that f'(x) = 2x, we see that the derivative is g'(x) f'(g(x)) = g'(x) * 2 g(x) = 2 g'(x) * x^(1/2).
We thus have two expressions for the derivative of the composite function f(g(x)). We can set these derivative equal and solve for the unknown function g'(x).
We set the two derivatives equal in the figure below and easily solve to find g'(x) = 1 / (2 x^(1/2)), as we expected.
As noted in your text, the same procedure can be followed to find the derivative of x^(1/n) for any integer value of n. The result will agree with the power function rule. It is then a short step to find the formula for the derivative of x^(m/n) for any integers m and n; the result again agrees with the power function rule so we will have extended the power function rule to include all rational number powers. The rule can then be extended to the irrational powers by arguments which are beyond the scope of this course, so that it applies to any real-number power.
As a final example we use the same procedure to find the derivative of the natural log function g(x) = ln(x). Its inverse function is f(x) = e^x.
As before, and as will be the case for any pair of inverse functions, we find the derivative of the composite function is 1.
Our other expression for the derivative of the composite will be g'(x) * f'(g(x)) = g'(x) * e^(g(x)) = g'(x) e^(ln x) = g'(x) * x.
Setting the two expressions for the derivative of the composite function equal we easily obtain the equation and solution below.
Note that it is always easier to use g(x) to represent the function whose derivative we do not know than to use f(x) for this function. This is because the expression for the desired derivative g'(x) sort of 'pops out' at us when we apply the chain rule. You might consider trying to run through the proof using f(x) to represent the function with unknown derivative. We can often infer what the function f'(x) must be, but since it appears only as f'(g(x)), at best we have to do some careful thinking to find formula for f'(x), and at worst we are going to get completely bumfuzzled by the attempt.
"